
Физика / ОПТИКА_методичка
.pdf
Министерство образования Республики Беларусь Учреждение образования
«Белорусский государственный университет информатики и радиоэлектроники»
Кафедра физики
ОПТИКА, АТОМНАЯ И КВАНТОВАЯ ФИЗИКА
Учебно-методический комплекс по курсу «Физика»
ДЛЯ СТУДЕНТОВ ВСЕХ СПЕЦИАЛЬНОСТЕЙ ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ
Минск 2005
УДК 53(075.8) ББК 22.3 я 73
O 62
Авторы:
В.В. Аксенов, А.В. Березин, В.А. Морозов, Ю.И. Савилова.
Оптика, атомная и квантовая физика: Учебно-методический комплекс по курсу «Физика» для студ. всех спец. БГУИР заоч. формы обуч.
О62 /В.В. Аксенов, А.В. Березин, В.А. Морозов, Ю.И. Савилова. – Мн.:
БГУИР, 2005. – 84 с.: ил.
ISBN 985-444-767-7
Учебно-методический комплекс является продолжением ранее изданных учебно-методических материалов по разделам: «Механика, механические колебания и упругие волны, молекулярная физика и термодинамика» и «электричество и магнетизм. Представленная работа включает в себя разделы: оптика, квантовая механика, физика твердого тела, атомная и ядерная физика. Учтены особенности учебных планов заочного факультета БГУИР, даны основные формулы, примеры решения задач по каждой теме и контрольные задания.
УДК 53(075.8) ББК 22.3 я 73
|
Коллектив авторов, 2005 |
ISBN 985-444-767-7 |
БГУИР, 2005 |
СОДЕРЖАНИЕ ПРОГРАММЫ КУРСА
ОПТИКА
Световая волна. Показатель преломления среды. Законы геометрической оптики. Оптическая длина пути. Принцип Ферма. Интерференция. Принцип суперпозиции волн. Опыт Юнга. Понятие о когерентности. Временная и пространственная когерентность. Длина и радиус когерентности. Способы наблюдения интерференции света. Зеркала (или бипризмы) Френеля. Полосы равного наклона и равной толщины. Просветление оптики.
Дифракция. Принцип Гюйгенса-Френеля. Дифракция Френеля и дифракция Фраунгофера. Зоны Френеля. Дифракция Френеля от круглого отверстия и от круглого непрозрачного диска. Дифракция Фраунгофера от щели. Дифракционная решетка. Угловая дисперсия и разрешающая способность решетки.
Поляризация. Естественный и поляризованный свет. Степень поляризации. Поляризаторы и анализаторы. Закон Малюса. Поляризация при отражении и преломлении. Закон Брюстера. Эффект Керра. Вращение плоскости поляризации (оптическая активность). Магнитное вращение (эффект Фарадея).
КВАНТОВАЯ ФИЗИКА
Квантовая природа электромагнитного излучения. Классическая и квантовая теория равновесного теплового излучения. Формула Планка. Фотоэффект. Формула Эйнштейна. Фотоны. Импульс фотона. Эффект Комптона.
Волновые свойства микрочастиц. Гипотеза де Бройля. Опыты Дэвиссона и Джермера. Соотношения неопределенностей. Волновая функция, ее свойства. Уравнение Шредингера и его решение для частицы в бесконечно глубокой одномерной потенциальной яме. Решение уравнения Шредингера для гармонического осциллятора. Атом водорода. Периодическая система элементов.
Туннельный эффект. Поглощение, спонтанное и вынужденное излучение. Равновесное излучение. Принцип детального равновесия и формула Планка. Лазер (на примере трехуровневой системы).
Физика твердого тела. Физические типы кристаллических решеток. Теплоемкость кристаллов. Закон Дюлонга и Пти. Квантовая теория свободных электронов в металле. Распределение Ферми-Дирака. Энергетические зоны в кристаллах. Металлы, полупроводники, диэлектрики. Электропроводность металлов и полупроводников (собственная и примесная). Эффект Холла. Термоэлектрические явления. Полупроводниковые диоды и транзисторы. Сверхпроводимость. Магнитные свойства сверхпроводника (эффект Мейснера). Эффект Джозефсона. Высокотемпературная сверхпроводимость.
СТРОЕНИЕ И ФИЗИЧЕСКИЕ СВОЙСТВА ВЕЩЕСТВА
Физика ядра. Ядерные силы. Масса и энергия связи ядра. Радиоактивный распад. Ядерные реакции. Энергетическая схема ядерной реакции. Пути использования ядерной энергии. Элементарные частицы. Виды взаимодействия и классы элементарных частиц. Частицы и античастицы. Кварки.
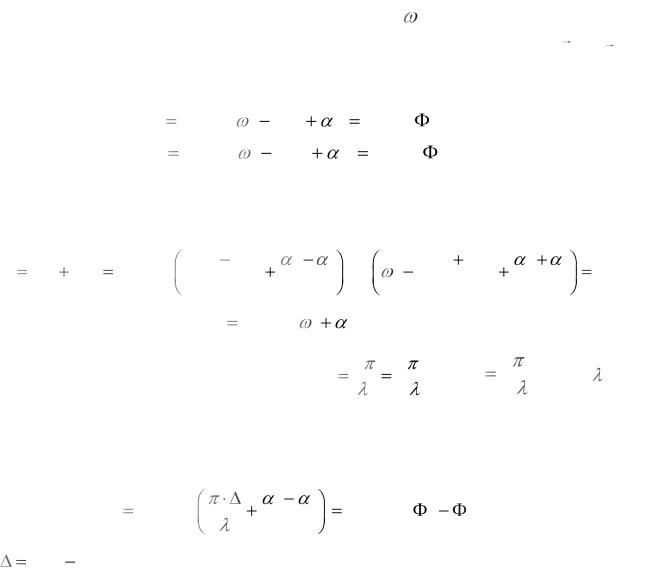
1. ИНТЕРФЕРЕНЦИЯ СВЕТА
Интерференция света – это явление перераспределения в пространстве световой энергии с образованием устойчивой во времени интерференционной картины чередования максимумов(Imax) и минимумов (Imin) интенсивности света при суперпозиции (наложении) двух или более когерентных волн.
Волны называются когерентными, если они имеют одинаковую частоту, по-
ляризацию и не зависящую от времени разность фаз в произвольной точке их
встречи.
Исследование интерференции волн сводится к определению разности фаз в
точке их наложения. Рассмотрим две волны частоты |
, с одинаковой (для про- |
|||||
стоты) амплитудой E0 и одинаковым направлением колебаний векторов E1 и E2 |
||||||
(например, вдоль Oy), распространяющиеся по оси Оx: |
|
|||||
E1 y |
E0 cos( |
t |
k1x1 |
1 ) |
E0 cos |
1, |
E2 y |
E0 cos( |
t |
k2 x2 |
2 ) |
E0 cos |
2 . |
Согласно принципу суперпозиции, напряженность результирующего поля в произвольной точке встречи волн равна их сумме:
E |
|
E |
E |
2E cos |
k2 x2 k1x1 |
|
2 |
1 |
cos t |
k2 x2 k1x1 |
|
2 |
1 |
y |
|
|
|
|
|
|
|
|
|||||
|
1y |
2 y |
0 |
2 |
2 |
|
|
2 |
|
|
2 |
||
|
|
|
|
|
|
|
|
|
|||||
Em cos |
t |
. |
|
|
|
|
|
|
|
|
Учитывая, что волновые числа равны |
k |
2 |
|
|
2 n1 |
и k |
|
2 n2 |
, где |
– |
|
|
|
|
2 |
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
длина волны в вакууме, n1 и n2 |
– показатели преломления сред, в которых рас- |
|||||||||||||
пространяются волны, запишем амплитуду Em суммарной волны в виде |
||||||||||||||
|
Em |
|
2E0 cos |
|
2 |
1 |
|
|
2E0 cos |
|
|
, |
||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2 |
|
|
2 |
1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
n2 x2 n1x1 – оптическая разность хода волн. |
|
|
|
||||||||||
Из-за большой частоты оптических колебаний напряженность E невозможно
измерить непосредственно. Все приемники излучения измеряют энергетические

величины, усредненные за промежуток времени, много больший периода оптиче-
ских колебаний.
Средняя по времени наблюдения интенсивность I волны, пропорциональна среднему значению квадрата ее амплитуды Em2 :
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
2 |
|
1 |
|
|
|
2 |
|
|
2 |
|
|
|
|
||
|
|
I |
Em |
|
|
4E0 |
cos |
|
|
|
|
|
|
|
|
|
|
|
4E0 cos |
|
2 |
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
2I |
0 cos |
2 |
|
|
|
|
|
|
2 |
|
1 |
|
|
|
2I0 cos |
2 |
|
|
|
1 , |
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где I0 – интенсивность каждой из накладываемых волн (т.к. амплитуды этих волн |
||||||||||||||||||||||||||||||||
одинаковы, то I1 I2 |
|
I0 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Интенсивность I результирующей волны зависит от разности хода |
и раз- |
|||||||||||||||||||||||||||||||
ности начальных фаз |
|
|
1 |
|
|
2 . Рассмотрим два случая: |
|
|
|
|
|
|
|
|||||||||||||||||||
1. При распространении некогерентных волн от независимых источников на- |
||||||||||||||||||||||||||||||||
чальные фазы |
1(t) и |
|
2 (t) являются случайными функциями времени, |
причем их |
||||||||||||||||||||||||||||
разность |
|
|
1 |
|
|
|
2 |
f (t) |
|
|
также |
изменяется |
|
со |
|
|
|
временем. |
Поэтому |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
cos2 |
|
|
1 |
|
, |
тогда |
|
E |
2 |
|
|
2E2 |
E2 |
E2 |
и интенсивность I результирую- |
|||||||||||||||||
|
1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
2 |
|
2 |
|
|
|
|
|
|
m |
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
щей волны складывается из интенсивностей I1 и I2 накладываемых волн: |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
I1 |
I2 |
2I0 . |
|
|
|
|
|
|
|
|
|
|||||
2. В случае наложения когерентных волн обе волны также имеют хаотически |
||||||||||||||||||||||||||||||||
меняющиеся фазы, |
но закон изменения |
1(t) |
и |
2 (t) |
одинаков, так как они отно- |
|||||||||||||||||||||||||||
сятся к |
одному и |
тому же |
|
фронту волны, т. |
е. |
1 |
2 |
|
(t) |
и их разность |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
2 |
0 (или const). Тогда разность фаз |
2 |
|
1 |
|
|
|
|
и, |
следовательно, |
|||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
квадрат амплитуды |
E2 результирующей волны определяется только значением |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оптической разности хода , которая не зависит от времени, вследствие чего знак усреднения можно убрать:

E2 |
4E2 cos2 |
|
|
|
|
2E2 |
1 |
cos |
2 |
|
|
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
m |
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, интенсивность I результирующей волны также определяется |
|||||||||||||||||||||||
только значением оптической разности хода |
, не зависящей от времени: |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
I0 |
|
|
2 1 |
cos |
2 |
|
|
|
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||
Из этого выражения следует, |
|
что при cos |
|
|
|
|
|
1 интенсивность результи- |
|||||||||||||||
|
|
|
|
|
2 |
||||||||||||||||||
рующей волны максимальна I |
Imax |
2I0 , а при cos |
|
|
|
1 интенсивность ре- |
|||||||||||||||||
|
|
|
|
||||||||||||||||||||
зультирующей волны минимальна I |
Imin |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Условие возникновения интерференционного максимума. |
|
||||||||||||||||||||||
В некоторой точке пространства интенсивность I |
|
результирующей световой |
|||||||||||||||||||||
волны принимает максимальное значение Imax, когда cos |
2 |
|
max |
1, тогда |
|||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
max |
2m |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
(1.1) |
||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где m 0, 1, 2, ... – порядок интерференции; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
или |
2 |
1 |
2m , |
где |
|
|
m |
0, |
|
1, |
2, ... . |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если в некоторой точке пространства две когерентные волны возбуждают ко-
лебания с одинаковыми фазами (волны приходят в эту точку в одинаковых фазах),
т. е. оптическая разность хода этих волн равна чѐтному числу полудлин волн, то в
этой точке наблюдается интерференционный максимум.
Условие возникновения интерференционного минимума.
В некоторой точке пространства интенсивность I результирующей световой
волны принимает минимальное значение Imin, когда cos |
2 |
min |
1, тогда |
|||
|
||||||
|
|
|||||
min |
(2m 1) |
|
, |
|
|
(1.2) |
2 |
|
|
||||
|
|
|
|
|
||
|
|
|
|
|
|
|
где m 0, 1, 2, ... ;
или |
2 |
1 |
(2m 1) , где m 0, 1, 2, ... . |
|
|
Если в некоторой точке пространства две когерентные волны возбуждают ко-
лебания с противоположными фазами (волны приходят в эту точку в противофа-
зах), т. е. оптическая разность хода этих волн равна нечѐтному числу полудлин волн, то в этой точке наблюдается интерференционный минимум.
Полученные результаты позволяют рассчитать параметры интерференцион-
ной картины, полученной в результате наложения двух когерентных волн от ис-
точников S1 и S2 , расстояние между которыми d (Рис. 1).
y
|
|
|
y |
|
|
|
P |
|
S1 |
|
|
|
. |
|
y |
|
|
I (y) |
|
d |
. |
|
O |
|
|
||
|
|
L |
|
|
|
|
|
|
S2 |
|
Э |
|
|
|
|
|
|
|
Рис.1 |
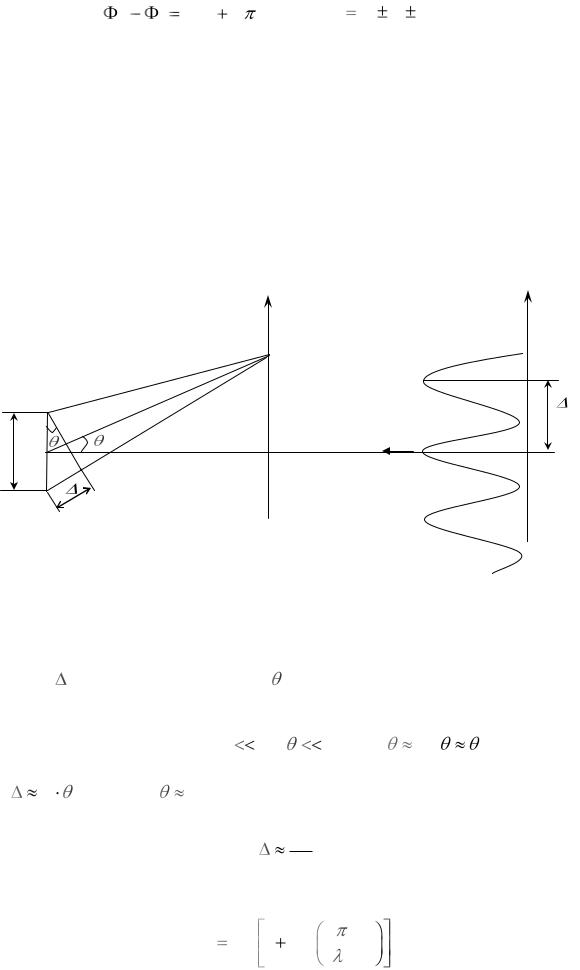
Чтобы найти зависимость распределения интенсивности I на экране Э от ко-
ординаты y точки наблюдения Р, необходимо выразить через эту координату раз-
ность хода . Для этого введем угол , образуемый направлением на точку Р с
перпендикуляром к линии, соединяющей источники (т. е. с «оптической осью»
рассматриваемой схемы). |
Если d |
L , |
1, то tg sin |
и разность хода |
|||
равна |
d . Так как |
|
y |
, то |
|
|
|
|
L |
|
|
|
|||
|
|
|
|
|
|
|
|
ydL .
И для амплитуды получим
I ( y) 2I0 1 cos |
2 d |
y . |
|
L |
|||
|
|

Ширина интерференционных полос или пространственный период интер-
ференционной картины – это расстояние y |
между соседними максимума или |
||||||
минимумами. Найдем координату m-го максимума, учитывая, что |
max |
2m |
|
, где |
|||
2 |
|||||||
|
|
|
|
|
|||
|
|
|
|
|
|
||
m 0, 1, 2, ... : |
|
|
|
|
|
|
|
ymax |
mL |
. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|||
m |
d |
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда следует, что
|
y |
ymax |
ymax |
y |
|
|
|
|
L |
. |
|
|
|
|
|||
|
max |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
m 1 |
|
m |
|
|
|
d |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найдем |
координату m-го |
минимума, |
учитывая, |
что |
min |
(2m 1) |
|
, где |
|||||||||
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
m 0, 1, 2, ... : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
ymin |
|
(2m |
1)L |
. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
m |
|
2d |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отсюда следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
ymin |
ymin |
y |
|
|
|
L |
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
m 1 |
|
m |
min |
|
|
d |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Измеряя |
y , можно найти . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. ДИФРАКЦИЯ СВЕТА
При определенных условиях световые волны (как и другие волны) могут от-
клоняться от своего прямолинейного распространения.
Дифракция – это совокупность явлений, наблюдаемых при распространении света в среде с резко выраженными неоднородностями (размеры которых ~ 
 r ,
r ,
где r – расстояние до точки наблюдения), проявляющихся в перераспределении световой энергии в пространстве в результате суперпозиции волн.
В узком понимании дифракция – это огибание волнами препятствий и про-
никновение их в область геометрической тени (отклонение распространение волн вблизи препятствий от законов геометрической оптики).
Для наблюдения дифракции световых волн необходимы специальные усло-
вия, обусловленные малостью их длин волн. Обычно на пути световой волны по-
мещают непрозрачную преграду, закрывающую часть световой волны. За прегра-
дой помещают экран, на котором при определенных условиях возникает дифрак-
ционная картина в виде той или иной системы чередования полос или пятен – максимумов и минимумов освещенности.
Различают два вида дифракции:
1. Дифракция Френеля – источник и точка наблюдения находятся на конеч-
ном расстоянии от препятствия (дифракция в расходящихся пучках).
2. Дифракция Фраунгофера – на бесконечном расстоянии (дифракция в па-
раллельных пучках).
2.1. Принцип Гюйгенса-Френеля
Строгая теория дифракции основана на решении системы уравнений Мак-
свелла. Приближенный метод решения задач о распространении волн основан на принципе Гюйгенса-Френеля, согласно которому все элементы поверхности, че-
рез которую в данный момент времени проходит фронт волны, становятся источ-
никами когерентных вторичных волн, а волновая поверхность в любой после-
дующий момент времени является результатом интерференции (наложения) этих вторичных волн. Таким образом, между интерференцией и дифракцией нет прин-
ципиального различия. Исторически принято называть интерференцией суперпо-
зицию волн от конечного числа дискретно расположенных когерентных источни-
ков волн, а дифракцией – от бесконечного числа непрерывно расположенных ко-
герентных источников.
Запишем математическое выражение принципа Гюйгенса-Френеля. Результи-
рующее возмущение в точке Р является суперпозицией возмущений, исходящих от участков dS волновой поверхности S (Рис. 2):
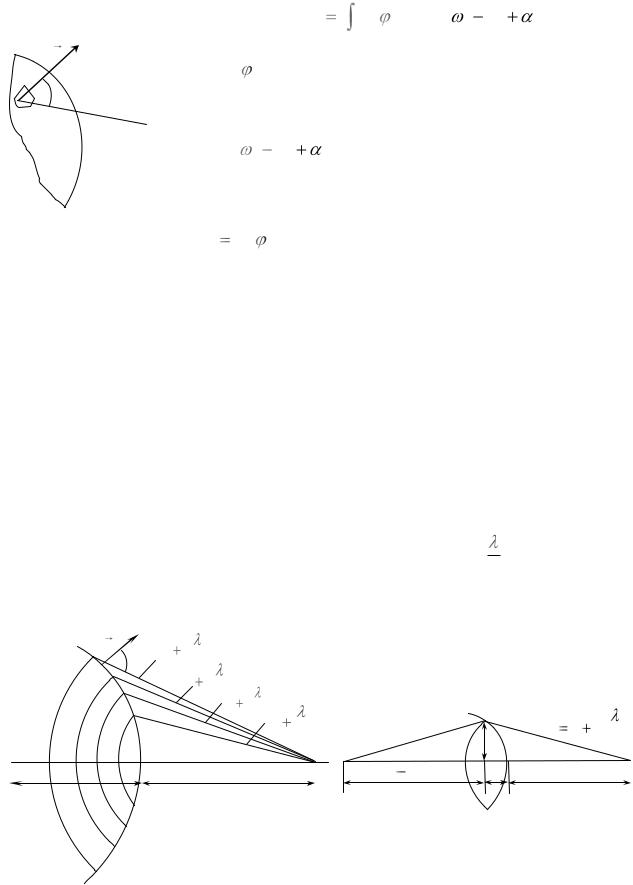
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
K ( ) |
a0 |
cos( t кr |
)dS , |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(S ) |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
где K ( |
) |
– коэффициент, обусловленный поперечностью |
||||||||||
|
φ |
r |
. |
волны; |
|
|
|
|
|
|
|
|
|
||||
dS |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a0 |
|
cos( |
t |
|
кr |
) – сферическая волна на расстоянии r |
|||||
|
|
|
|
|
|
r |
|||||||||||
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
от dS ; |
|
|
|
|
|
|
|
|
|
|||
Рис. 2 |
|
|
|
|
|
|
|
a |
|
|
|
|
|
||||
|
|
|
|
|
dE |
K ( |
) |
0 |
dS |
– амплитуда возмущения от dS . |
|||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
0 |
|
|
r |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вычисления по данной формуле сложны, однако, в случаях, имеющих сим-
метрию, сводятся к простому алгебраическому или геометрическому суммирова-
нию.
2.2. Дифракция Френеля
Для учета интерференции вторичных волн Френель предложил мысленно разбить волновую поверхность в месте расположения преграды (например, круг-
лое отверстие на экране Э) на кольцевые зоны по следующему правилу: расстоя-
ния от краев соседних зон до точки P должны отличаться на 2 (Рис. 3 а).
|
|
n |
b 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
φ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
b 3 |
|
b 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 b |
|
|
|
|
a |
bm |
b |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||
S |
|
|
|
O |
P |
|
S |
rm O |
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
.a |
|
|
|
|
|
|
|
|
b |
|
|
. a hm |
hm |
b |
|
|
|
P |
|||||
|
|
|
|
|
1-я зона |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2-я зона |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
3-я зона |
|
|
|
|
|
б) |
|
|
|
|
|
||||||||||
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4-я зона |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Рис. 3
