Соотношение Майера

Сначала рассмотрим закон, описывающий этот процесс и его график в координатах (P,V).

Рис. 3

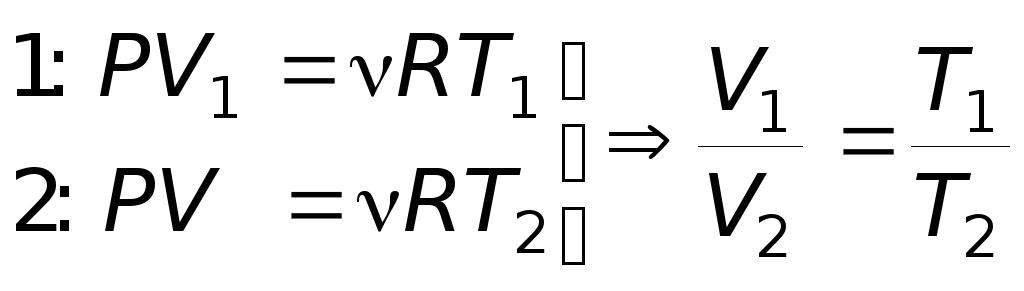- закон Гей-Люссака.

Теперь работа, совершаемая газом,

первое начало термодинамики для изобарического процесса.

приращение внутренней энергии газа тоже не равно нулю , и первое начало термодинамики не меняет своего вида:

Формула для подсчёта теплоты теперь примет вид

где - молярная теплоёмкость газа при постоянном давлении.

Приращение внутренней энергии запишем в виде

Работу, совершаемую газом, также представим в аналогичном виде

.

Здесь мы воспользовались уравнением Менделеева-Клапейрона

дифференциальное уравнение которого при дает

.

Из выражения для работы следует размерность и физический смысл универсальной газовой постоянной R:

, .

Универсальная газовая постоянная R численно равно работе, совершённой одним молем газа при изобарическом процессе при увеличении его температуры на один градус.

Продолжим рассмотрение изобарического процесса. Подставляя полученные выражения для dQ, dU, dA в первое начало термодинамики, получим:

Сокращая на dT, получим соотношение между молярными теплоёмкостями газа при постоянном объёме и постоянном давлении :

- соотношение Майера.

Учитывая выражение для , получим аналогичное выражение для

=.

Приведем также выражение для отношения молярных теплоёмкостей и

.

Для двухатомных молекул при невысоких температурах i = 5, тогда 1,4.

Выпишем работу, совершаемую газом при изобарическом процессе (P=const):

Рис. 4

работа, совершаемая газом при изобарическом процессе.

-

На графике (P,V) работа, совершаемая газом, численно равна площади прямоугольника, построенного под изобарой.

3. Термодинамика изотермического процесса: T=const.

Приведем закон, описывающий этот процесс, и его график в координатах (P,V).

Рис. 5

закон Бойля-Мариотта

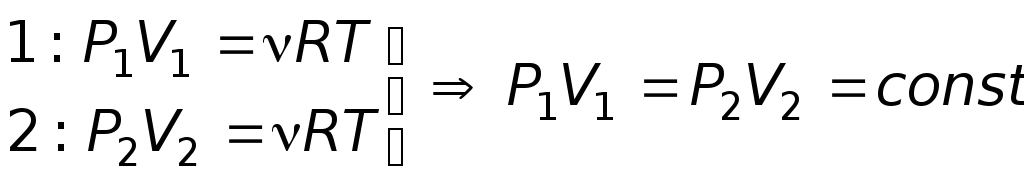Так как T = const, то

т. е. dU = 0 - изменение внутренней энергии газа при изотермическом процессе равно нулю.

Первое начало термодинамики при изотермическом процессе

Тогда

dQ = dA -

При изотермическом процессе вся теплота, сообщенная газу, идет на работу, совершаемую газом: Q = A.

Выпишем работу, совершаемую газом при изотермическом процессе. Используя уравнение Менделеева-Клапейрона представим элементарную работу в виде:

Тогда

.

работа, совершаемая газом при изотермическом процессе

Рис. 6

Учитывая то, что при изотермическом процессе работу можно вычислить также по формуле:

;

На графике (P,V) работа, совершаемая газом, численно равна площади под кривой, описывающий изотермический процесс.

4. Термодинамика адиабатического процесса: dQ=0

Несмотря на то, что мы поочерёдно рассмотрели процессы с V=const, P=const, T=const, список характерных газовых процессов этим не исчерпывается. Обратим внимание, что при изохорическом процессе dA=0, при изотермическом процессе dU=0, и поэтому естественно рассмотреть процесс в котором dQ=0, т.е. адиабатический процесс.

Адиабатический процесс - это процесс, протекающий без теплообмена с окружающей средой.

Поскольку dQ = 0, то первое начало термодинамики примет вид:

первое начало термодинамики при адиабатическом процессе

-

Такой вид первого начала термодинамики позволяет легко вычислить работу, совершаемую газом:

или для конечного адиабатического процесса:

-

- работа, совершаемая газом при адиабатическом процессе.

Исходя из dU + dA = 0, выведем закон, которому удовлетворяют параметры газа при адиабатическом процессе. Для этого dU и dA представим в виде

Подставив это выражение в dU + dA = 0, получим дифференциальное уравнение:

которое, разделив на С_V T и используя соотношения

,

можно записать в виде

.

Это дифференциальное уравнение приводится к полному дифференциалу:

Решение этого дифференциального уравнения имеет вид

уравнение адиабатического процесса в переменных(T,V)

или

-

Воспользовавшись уравнением Менделеева-Клапейрона PV = RT, можно перейти к переменным (P,V) и (T,P).

Например, из Подставляя это в уравнение , получим

или

- уравнение Пуассона,

где -коэффициент Пуассона.

Рис. 7

- уравнения адиабаты.