Эл.поле
.doc
|
|
|
|
Интегральная и дифференциальная форма закона полного тока |
|
|
Количественная
связь между циркуляцией вектора
Линейный интеграл от напряженности магнитного поля вдоль любого замкнутого контура равен полному току, пронизывающему замкнутый контур. Интегральную форму закона полного тока применяют, когда может быть использована симметрия в поле. Определим напряженность поля в некоторой точке А в поле уединенного прямого провода с током I (рис. 17.3).
Рис. 17.3. к определению напряженности поля уединенного провода Проведем через точку А окружность радиусом R в плоскости, перпендикулярной оси провода, так что центр ее находится на этой оси. В силу симметрии напряженность поля во всех точках окружности численно одна и та же. Направление напряженности совпадает с касательной к окружности:
Если какое-либо поле имеет сложный характер и напряженность H нельзя вывести из-под знака интеграла, то использовать закон полного тока в интегральной форме так просто не удается. Соотношение (17.3) пригодно для контура любых размеров, в том числе и для весьма малого.
Выделим
в какой-либо среде небольшой контур
и составим вдоль него циркуляцию
вектора
Рис.
17.4. К нахождению циркуляции вектора
Если
площадь мала, то можно полагать, что
плотность тока
Разделим обе части равенства на s и устремим s к нулю. Возьмем предел полученного соотношения:
Если
площадь
Формула (17.6) называется законом полного тока в дифференциальной форме. Ротор – это функция, характеризующая поле в рассматриваемой точке, в отношении способности к образованию вихрей. Раскрытие функции ротора в декартовой системе координат мы рассмотрели в параграфе 14.1.3 формулы (12.17), (12.18) и (12.19).
|
|
|
|
|
Принцип непрерывности магнитного потока и запись его в дифференциальной форме |
|
|
Магнитный поток – это поток вектора магнитной индукции через некоторую поверхность:
Если поверхность замкнута, то
Это математическая запись принципа непрерывности магнитного потока. Разделим обе части (17.8) на объем V, находящийся внутри замкнутой поверхности s, и найдем предел отношения, когда V стремится к нулю:
Соотношение
(17.9) можно трактовать как дифференциальную
форму принципа непрерывности магнитного
потока. В любой точке магнитного поля
нет ни истока, ни стока линий вектора
магнитной индукции. Линии вектора
|
||
|
|
Скалярный потенциал магнитного поля |
|
|
Вихревыми
принято называть поля, в которых ротор
векторной величины, описывающей поле,
отличен от нуля. Так, для магнитного
поля постоянного тока
Так
как
Скалярный
потенциал магнитного поля
Разность скалярных магнитных потенциалов между точками 1 и 2 называют падением магнитного напряжения между точками 1 и 2. Граничные условия В магнитном поле постоянного тока выполняются следующие граничные условия:
На границе раздела двух однородных и изотропных сред, различных в магнитном отношении (различные r) равны тангенциальные составляющие векторов напряженности магнитного поля и нормальные составляющие магнитных индукций на границе раздела. Условие (17.12) не выполняется, если на поверхности раздела двух сред протекает так называемый поверхностный ток. Под ним понимают ток, протекающий по бесконечно тонкому плоскому проводнику, положенному на границе раздела.
|
|
|
|
|
Векторный потенциал магнитного поля |
|
|
Векторный
потенциал магнитного поля
Основанием для представления индукции в виде ротора от вектора-потенциала служит то, что дивергенция любого ротора тождественно равна нулю, т.е.
Если вектор-потенциал как функция координат известен, то индукцию в любой точке поля определяют путем нахождения ротора от вектора-потенциала в соответствии с (17.13). Векторным потенциалом можно пользоваться и для областей, занятых током. В электротехнических расчетах векторный потенциал применяют для двух целей: 1. Определения вектора магнитной индукции по формуле (17.13); 2. Определения магнитного потока, пронизывающего какой-либо контур. Векторный потенциал в произвольной точке поля связан с плотностью тока в этой же точке уравнением Пуассона. Умножим обе части (17.6) на a. Если магнитная проницаемость постоянна, то ее можно внести под знак ротора:
rot rot A = [V[VA]] = grad div A - V2A = mad.
Так
как
Это
требование означает, что линии вектора
Уравнение
(17.16) представляет собой уравнение
Пуассона. В отличие от уравнения
(13.21), составленного относительно
скалярной величины ,
уравнение (17.16) составлено относительно
векторной величины
Единицей
измерения
|
|
|
|
|
Выражение магнитного потока через циркуляцию вектора-потенциала |
|
|
Магнитный поток, пронизывающий какую-либо поверхность:
На основании теоремы Стокса поверхностный интеграл может быть преобразован в линейный
Для
определения магнитного потока,
пронизывающего некоторую площадь
(поверхность) s,
необходимо подсчитать циркуляцию
вектора потенциала
Определение
потока по (17.18) часто имеет преимущества
по сравнению с определением потока
через магнитную индукцию (17.7).
Соотношением (17.7) можно пользоваться
в том случае, когда известно значение
Рассмотрим граничные условия для векторного потенциала.
|
|
|
|
|
|
|
Расчет магнитного поля одиночного проводника с током |
|
|
Требуется рассчитать магнитное поле внутри и за пределами проводника (рис. 17.5). Это означает, что необходимо определить распределение напряженности и вектора-потенциала.
Рис. 17.5. К расчету магнитного поля одиночного проводника Для расчета используем закон полного тока в интегральной форме
Рассчитаем
циркуляцию вдоль окружности, центр
которой совпадает с центром провода.
При этом напряженность в любой точке
этой окружности
Внутри
проводника ( Следовательно, внутри проводника напряженность магнитного поля определяется выражением
Максимальное значение напряженности магнитного поля имеет место на поверхности проводника
Вне
проводника (
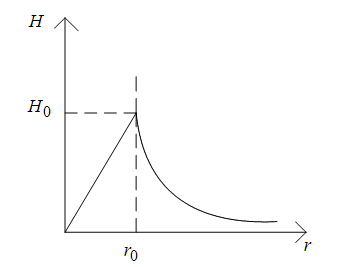
Распределение напряженности магнитного поля внутри и вне проводника показано на рис. 17.6.
Рис. 17.6. Распределение магнитного поля одиночного проводника
Рассчитаем
вектор-потенциал внутри проводника
( Вектор-потенциал образует плоско параллельное поле, изменяющееся только по радиусу. Поэтому в цилиндрической системе координат уравнение Пуассона запишется
Проинтегрировав его, получим
Так как поблизости нет другого поля, то постоянную интегрирования C1 можно приравнять к нулю. Тогда
В свою очередь,
При
r
= 0
Проинтегрировав уравнение (17.21)*, получим
Если принять, что на поверхности проводника A1 = 0, то постоянная интегрирования C2 будет равна
Тогда
Так
как за пределами проводника тока нет,
то вектор-потенциал подчиняется
уравнению Лапласа
Используя то же допущение о плоско параллельном поле, получим
На поверхности провода по закону полного тока
Следовательно,
Из
условия непрерывности вектора-потенциала
следует, что при
Тогда
Выделим в толще проводника элементарную площадку, нормаль к которой параллельна вектору напряженности (рис. 17.7).
Рис. 17.7. К расчету вектора-потенциала магнитного поля одиночного проводника с током По теореме Стокса
Этот интеграл распадается на 4 составляющие
На
участках 2-3 и 4-1 векторы
Индуктивность, обусловленная магнитным потоком внутри проводника
В свою очередь,
Тогда
За
пределами проводника (
|
||
|
|
Расчет индуктивности двухпроводной линии |
|
|
Рис. 17.8. К расчету индуктивности двухпроводной линии При расчете воспользуемся методом наложения.
Потокосцепления, создаваемые левым током
Такие же потокосцепления создаются правым током.
Для
линий электропередачи можно принять,
что
|
|
|
|
|
|
|
Взаимное соответствие электростатического и магнитного полей |
|
|
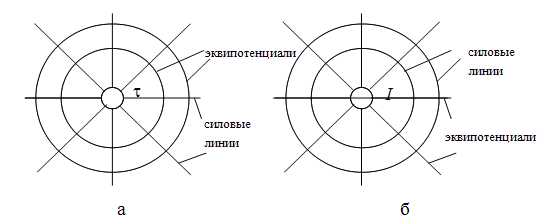
Между картинами электростатического и магнитного полей постоянного тока в областях, не занятых током, может быть соответствие двух типов: 1. Когда одинаково распределение линейных зарядов в электростатическом поле и линейных токов в магнитном поле. В этом случае картины полей подобны. Отличие лишь состоит в том, что силовым линиям электростатического поля отвечают эквипотенциальные линии магнитного поля, а эквипотенциалям электростатического поля – силовые линии магнитного. На рис. 17.9а изображена картина электрического поля, образованного уединенным линейным зарядом +τ, а на рис. 17.9б – картина магнитного поля уединенного проводника с током I. 2. Когда одинакова форма граничных эквипотенциальных поверхностей в электростатическом и магнитном полях постоянного тока. В этом случае картина поля оказывается совершенно одинаковой.
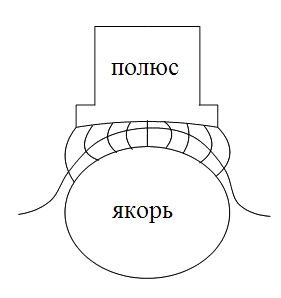
Рис. 17.9. Картина электростатического (а) и магнитного (б) полей Соответствие второго типа показано на рис. 17.10. На нем изображена картина магнитного поля в воздушном промежутке между полюсом и якорем машины постоянного тока. Если допустить, что полюс и якорь этой машины используют в качестве электродов некоторого конденсатора, то картина электрического поля в воздушном промежутке между электродами соответствовала бы картине магнитного поля.
Рис. 17.10. Картина электрического и магнитного полей при одинаковых граничных эквипотенциальных поверхностях
|
|
|
|
|
Задачи расчета магнитных полей. Общая характеристика методов расчета и исследования магнитных полей |
|
|
1. Определение индуктивности какого-либо контура или взаимной индуктивности двух контуров. 2. Определение сил, действующих в магнитном поле на движущийся электрон, неподвижный проводник с током, ферромагнитные массы в магнитном поле. 3. Расчет поля, создаваемого заданным распределением токов в пространстве. 4. Расчет магнитных экранов. Магнитными экранами называют устройства, предназначенные для ослабления магнитного поля в заданной области пространства по сравнению с магнитным полем вне экрана. 5. Нахождения распределения токов в некотором объеме для получения заданной картины магнитного поля. Методы расчета и исследование магнитных полей можно подразделить на три группы: – аналитическую, – графическую, – экспериментальную. Группу аналитических методов объединяют все чисто аналитического порядка приемы интегрирования уравнения Пуассона (для областей, занятых током), уравнения Лапласа (для областей, не занятых током), применение методов зеркальных и конформных отображений. В силу трудностей математического характера классические аналитические методы позволяют решать относительно небольшой круг задач. В особо трудных случаях прибегают к графическому методу построения картины поля или к исследованию магнитного поля на модели. Графические методы применимы к двухмерным безвихревым полям. В последние годы применяют метод интегральных уравнений, предполагающий использование ЭВМ и значительно расширяющий круг решаемых задач.
|
|
|
http://toe-kgeu.ru/toe3/359-toe3




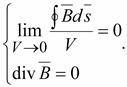 (17.9)
(17.9) (17.11)
(17.11) (17.12)
(17.12)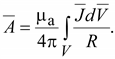 (17.17)
(17.17)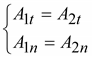 .
(17.19)
.
(17.19)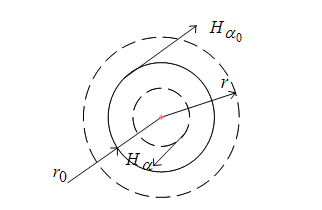
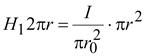 .
. .
.
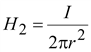 .
.
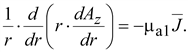 (17.20)
(17.20)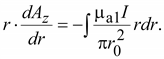 (17.22)
(17.22)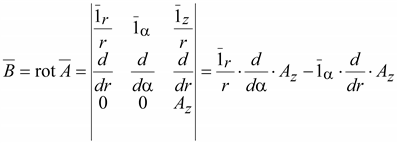 .
. (17.23)
(17.23)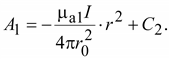 (17.24)
(17.24)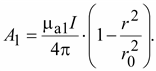 (17.25)
(17.25)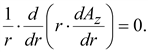 (17.26)
(17.26)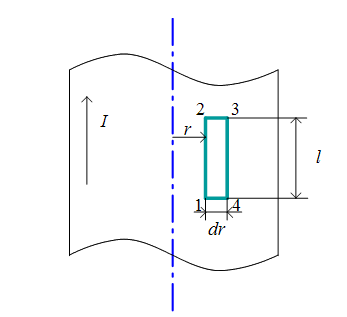
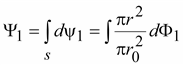 (17.33)
(17.33)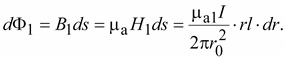 (17.34)
(17.34)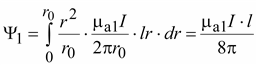 ;(17.35)
;(17.35)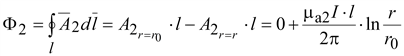
 (17.37)
(17.37)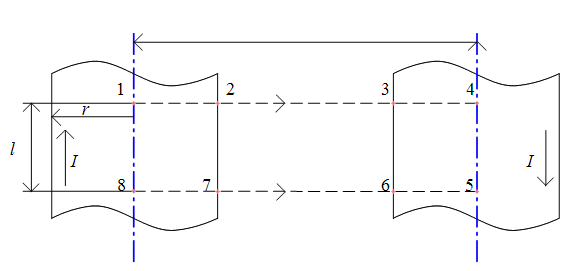
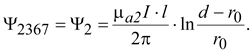
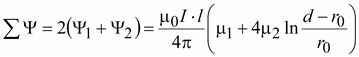 (17.38)
(17.38)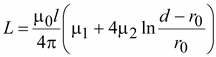 (17.39)
(17.39)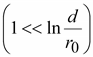 ,
получим индуктивность ЛЭП
,
получим индуктивность ЛЭП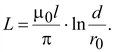 (17.40)
(17.40)