
- •Методичні вказівки до лабораторних робіт і самостійної роботи з курсу Комп'ютерна схемотехніка
- •Загальні положення
- •Лабораторна робота №1
- •Теоретичні відомості.
- •Відомості про навчальний стенд
- •Порядок виконання завдання 1
- •Лабораторна робота №2
- •Теоретичні відомості.
- •Повний дешифратор
- •Аналітичний підхід у проектуванні повних дешифраторів.
- •Неповні дешифратори
- •Порядок виконання завдання 2.1
- •Порядок виконання завдання 2.2
- •Контрольні запитання
- •Лабораторна робота №3
- •Теоретичні відомості.
- •Контрольні запитання
- •Лабораторна робота №4
- •Теоретичні відомості.
- •Порядок виконання завдання 1
- •Контрольні запитання
- •Лабораторна робота №5
- •Теоретичні відомості.
- •Лабораторна робота №6
- •Теоретичні відомості.
- •Порядок виконання завдання 6.1.1.
- •Порядок виконання завдання 6.1.2.
- •Порядок виконання завдання 6.2.1
- •Порядок виконання завдання 6.2.2.
- •Контрольні запитання
- •Лабораторна робота № 7 Проектування та дослідження лічильників
- •Теоретичні відомості.
- •Порядок виконання завдання 7.1.
- •Порядок виконання завдання 7. 2.
- •Контрольні запитання
- •Лабораторна робота №8
- •Теоретичні відомості.
- •2) Спосіб попереднього запису коду.
- •3) Спосіб збільшення модуля на одиницю (від до).
- •4) Спосіб побудови двійково-кодованого лічильника як цифрового автомату.
- •Порядок виконання завдань 8.1-8.3.
- •Контрольні питання
- •Лабораторна робота №9
- •Теоретичні відомості.
- •Рекомендована література
Неповні дешифратори
Неповним називається дешифратор з n-входами кількість виходів якого (N) відповідає умові N<2n.
Крім того, в багатьох випадках неповні дешифратори не є дешифраторами унітарного коду і передбачають можливість формування активного значення на одному виході при декількох значеннях вхідного коду або формування активних значень на декількох виходах для однієї комбінації вхідного коду. Неповні дешифратори не випускаються серійно у вигляді окремих модулів, оскільки існує велике різноманіття можливих варіантів їх побудови. Розробка неповного дешифратора ведеться з урахуванням особливостей функцій, що повинні виконуватись ним в конкретній схемі.
В процесі розробки неповного дешифратора можна виділити такі основні етапи:
складання таблиці відповідності (істиності) дешифратора;
мінімізація функцій вихідних сигналів;
побудова схеми дешифратора за отриманими функціями вихідних сигналів.
Розглянемо приклад розробки неповного дешифратора для формування активного значення вихідного сигналу у=1 при вхідних значеннях : 46h, 6Fh, A7h.
Переведемо наведені шістнацядкові значенння в двійковий код:
46h=0010 0110;
6Fh,=0110 1111;
A7h=1010 0111.
На підставі отриманих двійкових значень можна скласти таблицю істинності дешифратора, але, фактично, ми вже маємо дані про імпліканти одиниці (значення, на яких функція приймає значення логічної одиниці), для вибірки яких, як правило, і використовується таблиця істинності. Тому безпосередньо перейдемо до мінімізації функції для побудови дешифратора.
Спочатку запишемо її у вигляді досконалої диз’юнктивної форми:
![]()
Винесемо
постійні значення змінних за дужки
(тобто, ![]() ):
):
![]()
Для мінімізації значення в дужках побудуємо карту Карно:
|
х3х0 х7х6 |
00 |
01 |
11 |
10 |
|
0 |
1 |
|
|
|
|
01 |
|
|
1 |
|
|
11 |
|
|
|
|
|
10 |
1 |
|
|
|
За допомогою карти Карно значення в дужках мінімізується і функція у матиме наступний вигляд:
![]() (2.3)
(2.3)
Будуємо схему електричну функціональну неповного дешифратора за функцією 2.3.
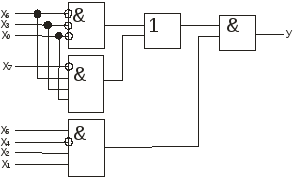
Рисунок 2.2 – Схема електрична функціональна неповного дешифратора
Кількість рівнів в схемі неповного дешифратора, наведеній на рисунку 2.3, можна зменшити, якщо в рівнянні 2.3 розкрити дужки (проаналізувати самостійно).
Примітка: Якщо створюваний неповний дешифратор формує активне значення вихідого сигналу лише при одній комбінації вхідного коду, як це передбачено завданням лабараторної роботи, мінімізація функції вихідного сигналу не виконується, оскільки єдина комбінація спрацьовування дешифратора не допускає можливості скорочення змінних (проаналізувати самостійно).
Завдання 2.1.
На базі стандартних елементів мікросхем ТТЛ і ТТЛШ логіки розробити повний двохадресний дешифратор. Значення активного рівня вихідних сигналів і перелік логічних елементів, що можуть бути використані при проектуванні дешифратора, наведені в таблиці 2.4.
Таблиця 2.4.
|
№ вар. |
Активний рівень уі |
Перелік та кількість наявних логічних елементів | |||||||||
|
2І |
3І |
4І |
2І-НЕ |
3І-НЕ |
4І-НЕ |
2АБО |
2АБО- НЕ |
3АБО- НЕ |
НЕ | ||
|
|
1 |
4 |
|
|
|
|
|
|
|
|
6 |
|
|
0 |
|
|
|
|
|
|
4 |
|
|
6 |
|
|
1 |
|
|
|
|
|
|
|
4 |
|
6 |
|
|
0 |
|
|
|
4 |
|
|
|
|
|
6 |
|
|
1 |
3 |
1 |
|
|
|
|
|
|
|
6 |
|
|
0 |
|
1 |
|
|
|
|
3 |
|
|
6 |
|
|
1 |
|
1 |
|
|
|
|
|
3 |
|
6 |
|
|
0 |
|
1 |
|
3 |
|
|
|
|
|
6 |
|
|
1 |
3 |
|
1 |
|
|
|
|
|
|
6 |
|
|
0 |
|
|
1 |
|
|
|
3 |
|
|
6 |
|
|
1 |
|
|
1 |
|
|
|
|
3 |
|
6 |
|
|
0 |
|
|
1 |
3 |
|
|
|
|
|
6 |
|
|
1 |
3 |
|
|
|
1 |
|
|
|
|
6 |
|
|
0 |
|
|
|
|
1 |
|
3 |
|
|
6 |
|
|
1 |
|
|
|
|
1 |
|
|
3 |
|
6 |
|
|
0 |
|
|
|
3 |
1 |
|
|
|
|
6 |
|
|
1 |
3 |
|
|
|
|
1 |
|
|
|
6 |
|
|
0 |
|
|
|
|
|
1 |
3 |
|
|
6 |
|
|
1 |
|
|
|
|
|
1 |
|
3 |
|
6 |
|
|
0 |
|
|
|
3 |
|
1 |
|
|
|
6 |
|
|
1 |
3 |
|
|
|
|
|
|
|
1 |
6 |
|
|
0 |
|
|
|
|
|
|
3 |
|
1 |
6 |
|
|
1 |
|
|
|
|
|
|
|
3 |
1 |
6 |
|
|
0 |
|
|
|
3 |
|
|
|
|
1 |
6 |
|
|
1 |
2 |
2 |
|
|
|
|
|
|
|
6 |
|
|
0 |
|
2 |
|
|
|
|
2 |
|
|
6 |
|
|
1 |
|
2 |
|
|
|
|
|
2 |
|
6 |
|
|
0 |
|
2 |
|
2 |
|
|
|
|
|
6 |
|
|
1 |
2 |
|
2 |
|
|
|
|
|
|
6 |
|
|
0 |
|
|
2 |
|
|
|
2 |
|
|
6 |
|
|
1 |
|
|
2 |
|
|
|
|
2 |
|
6 |
|
|
0 |
|
|
2 |
2 |
|
|
|
|
|
6 |
|
|
1 |
2 |
|
|
|
2 |
|
|
|
|
6 |
|
|
0 |
|
|
|
|
2 |
|
2 |
|
|
6 |
|
|
1 |
|
|
|
|
2 |
|
|
2 |
|
6 |
|
|
0 |
|
|
|
2 |
2 |
|
|
|
|
6 |
|
|
1 |
2 |
|
|
|
|
2 |
|
|
|
6 |
|
|
0 |
|
|
|
|
|
2 |
2 |
|
|
6 |
|
|
1 |
|
|
|
|
|
2 |
|
2 |
|
6 |
|
|
0 |
|
|
|
2 |
|
2 |
|
|
|
6 |
|
|
1 |
2 |
|
|
|
|
|
|
|
2 |
6 |
|
|
0 |
|
|
|
|
|
|
2 |
|
2 |
6 |
|
|
1 |
|
|
|
|
|
|
|
2 |
2 |
6 |
|
|
0 |
|
|
|
2 |
|
|
|
|
2 |
6 |
|
|
1 |
2 |
1 |
1 |
|
|
|
|
|
|
6 |
|
|
0 |
|
1 |
1 |
|
|
|
2 |
|
|
6 |
|
|
1 |
|
1 |
1 |
|
|
|
|
2 |
|
6 |
|
|
0 |
|
1 |
1 |
2 |
|
|
|
|
|
6 |
|
|
1 |
2 |
|
1 |
1 |
|
|
|
|
|
6 |
|
|
0 |
|
|
1 |
1 |
|
|
2 |
|
|
6 |
|
|
1 |
|
|
1 |
1 |
|
|
|
2 |
|
6 |
|
|
0 |
|
|
1 |
2 |
1 |
|
|
|
|
6 |
|
|
1 |
2 |
|
|
1 |
1 |
|
|
|
|
6 |
|
|
0 |
|
|
|
1 |
1 |
|
2 |
|
|
6 |
|
|
1 |
|
|
|
1 |
1 |
|
|
2 |
|
6 |
|
|
0 |
|
|
|
2 |
1 |
1 |
|
|
|
6 |
|
|
1 |
2 |
|
|
|
1 |
1 |
|
|
|
6 |
|
|
0 |
|
|
|
|
1 |
1 |
2 |
|
|
6 |
|
|
1 |
|
|
|
|
1 |
1 |
|
2 |
|
6 |
|
|
0 |
|
|
|
2 |
|
1 |
1 |
|
|
6 |
|
|
1 |
2 |
|
|
|
|
1 |
1 |
|
|
6 |
|
|
0 |
|
|
|
|
|
1 |
2 |
1 |
|
6 |
|
|
1 |
|
|
|
|
|
1 |
1 |
2 |
|
6 |
|
|
0 |
|
|
|
2 |
|
|
1 |
1 |
|
6 |
|
|
1 |
2 |
|
|
|
|
|
1 |
1 |
|
6 |
|
|
0 |
|
|
|
|
|
|
2 |
1 |
1 |
6 |
|
|
1 |
|
|
|
|
|
|
|
2 |
1 |
6 |
|
|
0 |
|
|
|
2 |
|
|
|
1 |
1 |
6 |
|
|
1 |
2 |
|
|
|
|
|
|
1 |
1 |
6 |
|
|
0 |
|
|
|
|
|
|
2 |
1 |
1 |
6 |
|
|
1 |
1 |
|
|
|
|
|
|
2 |
1 |
6 |
|
|
0 |
1 |
|
|
2 |
|
|
|
|
1 |
6 |
|
|
1 |
2 |
1 |
|
1 |
|
|
|
|
|
6 |
|
|
0 |
|
1 |
|
1 |
|
|
2 |
|
|
6 |
|
|
1 |
|
1 |
|
1 |
|
|
|
2 |
|
6 |
|
|
0 |
|
1 |
|
2 |
1 |
|
|
|
|
6 |
|
|
1 |
2 |
|
1 |
|
1 |
|
|
|
|
6 |
|
|
0 |
|
|
1 |
|
1 |
|
2 |
|
|
6 |
|
|
1 |
|
|
1 |
|
1 |
|
|
2 |
|
6 |
|
|
0 |
|
|
1 |
2 |
|
1 |
|
|
|
6 |
|
|
1 |
2 |
|
|
1 |
|
1 |
|
|
|
6 |
|
|
0 |
|
|
|
1 |
|
1 |
2 |
|
|
6 |
|
|
1 |
|
|
|
1 |
|
1 |
|
2 |
|
6 |
|
|
0 |
|
|
|
2 |
1 |
|
1 |
|
|
6 |
|
|
1 |
2 |
|
|
|
1 |
|
1 |
|
|
6 |
|
|
0 |
|
|
|
|
1 |
|
2 |
|
|
6 |
|
|
1 |
|
|
|
|
1 |
|
1 |
2 |
|
6 |
|
|
0 |
|
|
|
2 |
|
1 |
|
1 |
|
6 |
|
|
1 |
2 |
|
|
|
|
1 |
|
1 |
|
6 |
|
|
0 |
|
|
|
|
|
1 |
2 |
1 |
|
6 |
|
|
1 |
|
|
|
|
|
1 |
|
2 |
1 |
6 |
|
|
0 |
|
|
|
2 |
|
|
1 |
|
1 |
6 |
|
|
1 |
2 |
|
|
|
|
|
1 |
|
1 |
6 |
|
|
0 |
1 |
|
|
1 |
|
|
2 |
|
|
6 |
|
|
1 |
1 |
|
|
1 |
|
|
|
2 |
|
6 |
|
|
0 |
1 |
|
|
2 |
|
|
|
|
|
6 |
|
|
1 |
2 |
1 |
|
|
1 |
|
|
|
|
6 |
|
|
0 |
|
1 |
|
|
1 |
|
2 |
|
|
6 |
|
|
1 |
|
1 |
|
|
1 |
|
|
2 |
|
6 |
|
|
0 |
|
1 |
|
2 |
1 |
|
|
|
|
6 |
|
|
1 |
2 |
|
1 |
|
|
1 |
|
|
|
6 |
|
|
0 |
|
|
1 |
|
|
1 |
2 |
|
|
6 |
|
|
1 |
|
|
1 |
|
|
1 |
|
2 |
|
6 |
|
|
0 |
|
|
1 |
2 |
|
1 |
|
|
|
6 |
|
|
1 |
2 |
|
|
1 |
|
|
1 |
|
|
6 |
|
|
0 |
|
|
|
1 |
|
|
2 |
|
1 |
6 |
|
|
1 |
|
|
|
1 |
|
|
1 |
2 |
|
6 |
|
|
0 |
|
|
|
2 |
1 |
|
|
1 |
|
6 |
|
|
1 |
2 |
|
|
|
1 |
|
|
1 |
|
6 |
|
|
0 |
|
|
|
|
1 |
|
2 |
1 |
|
6 |
|
|
1 |
|
|
|
|
1 |
|
|
2 |
1 |
6 |
|
|
0 |
|
|
|
2 |
|
1 |
|
|
1 |
6 |
|
|
1 |
2 |
|
|
|
|
1 |
|
|
1 |
6 |
|
|
0 |
|
|
|
|
|
1 |
2 |
|
1 |
6 |
|
|
1 |
|
|
|
|
|
1 |
|
2 |
1 |
6 |
|
|
0 |
1 |
|
|
2 |
1 |
|
|
|
|
6 |
|
|
1 |
2 |
1 |
|
|
|
1 |
|
|
|
6 |
|
|
0 |
|
|
1 |
|
|
|
2 |
1 |
|
6 |
|
|
1 |
|
|
|
1 |
|
|
|
2 |
1 |
6 |
|
|
0 |
1 |
|
|
2 |
|
|
|
|
1 |
6 |
Завдання 2.2.
Розробити неповний дешифратор для заданої адреси на 8 входів (х7 ... х0) та 1 вихід (у), використовуючи елементи стандарних мікросхем ТТЛ і ТТЛШ логіки. Значення адреси розрахувати за формулою:
Адреса=№ варіанта+11.
Активне значення вихідного сигналу та базові елементи для проектування дешифратора наведені в таблиці 2.5.
Примітка: Особливістю завдання є те, що прямі та інвертовані значення вхідних сигналів повинні подаватися лише на логічні елементи, що визначені як базові для відповідного варіанту. Тобто, перед базовими логічними елементами в схемі можуть включатися лише інвертори. Для об’єднання виходів базових логічних елементів і формування заданого значення вихідного сигналу, за потреби, можуть використовуватись будь-які логічні елементи.
Таблиця 2.5.
|
№ варіанта |
Активний рівень у |
Базовий елемент |
|
1, 11, 21, 31, 41, 51, 61, 71, 81, 91, 101, 111 |
1 |
2І |
|
2, 12, 22, 32, 42, 52, 62, 72, 82, 92, 102, 112 |
0 |
2АБО-НЕ |
|
3, 13, 23, 33, 43, 53, 63, 73, 83, 93, 103, 113 |
1 |
4І |
|
4, 14, 24, 34, 44, 54, 64, 74, 84, 94, 104, 114 |
0 |
3І-НЕ |
|
5, 15, 25, 35, 45, 55, 65, 75, 85, 95, 105, 115 |
1 |
3АБО-НЕ |
|
6, 16, 26, 36, 46, 56, 66, 76, 86, 96, 106, 116 |
0 |
4І-НЕ |
|
7, 17, 27, 37, 47, 57, 67, 77, 87, 97, 107, 117 |
1 |
2АБО |
|
8, 18, 28, 38, 48, 58, 68, 78, 88, 98, 108, 118 |
0 |
5АБО-НЕ |
|
9, 19, 29, 39, 49, 59, 69, 79, 89, 99, 109, 119 |
1 |
3І |
|
10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120 |
0 |
2І-НЕ |


