1. Функція розподілу та її властивості

Неперервну випадкову величину неможливо задати законом розподілу, аналогічним розглянутому раніше для дискретних випадкових величин. Існує спільний спосіб задання будь-якого типу величин (і дискретних, і неперервних) – за допомогою функції розподілу.

Функцією розподілу (інтегральною функцією) називається функція , яка визначає ймовірність того, що випадкова величинау результаті випробування прийме значення, менше, ніж:

.

З геометричної точки зору – це ймовірність того, що випадкова величинаприйме значення, яке зображається на числовій осі точкою, що лежить зліва від точки.

Відзначимо такі властивості функції розподілу.

1. Значення функції розподілу належать відрізку :

.

Це випливає з того, що як ймовірність події може приймати лише значення з множини.

2. Функція неспадна: якщо, то.

Дійсно, згідно з теоремою додавання ймовірностей несумісних подій, маємо

,

або

.

Оскільки останній доданок невід’ємний, то звідси випливає, що . Властивість 2) доведена.

Аналізуючи викладки, проведені при доведенні даної властивості, одержуємо таке

Правило. Ймовірність того, що випадкова величина прийме значення, яке знаходиться в інтервалі , дорівнює приросту функції розподілу на цьому інтервалі:

.

Зауважимо, що формально ймовірність того, що неперервна випадкова величина прийме одне певне значення, дорівнює нулю. Дійсно, нехай. Маємо:

.

Оскільки – неперервна функція, то при. Виходить, що ймовірність того, що, дорівнює нулю. Таким чином,

.

Згідно з класичним означенням ймовірності, виходить, що події неможливі. Але насправді це не так. При користуванні функцією розподілу ймовірностей ставлять питання не про визначення ймовірності події, а про те, щоприйме значення, яке належить інтервалу.

3. Якщо можливі значення випадкової величини належать інтервалу , топриіпри.

Якщо можливі значення неперервної випадкової величини розміщені на всій осі , то мають місце такі граничні рівності:

; .

Приклад. Знайти функцію розподілу для дискретної випадкової величини, заданої законом розподілу

	1	3	5
	0,2	0,3	0,5

Розв’язування. Маємо: при . При. При. При.

2. Щільність розподілу ймовірностей, її властивості та зв’язок з функцією розподілу

Неперервні випадкові величини характеризуються не тільки інтегральною, але і диференціальною функцією (щільністю розподілу).

Щільністю розподілу ймовірностей неперервної випадкової величини називають функцією , яка є першою похідною від функції розподілу : .

Неважко довести таку теорему.

Теорема. Ймовірність того, що неперервна випадкова величина прийме значення, що належить інтервалу, дорівнює визначеному інтервалу від щільності розподілу, взятому в межах віддо:

.

Дійсно, оскільки , а; то.

Знаючи функцію , легко знайти:

.

Це дійсно так, оскільки .

Приклад 2. Знаючи щільність розподілу , знайти функцію розподілу:

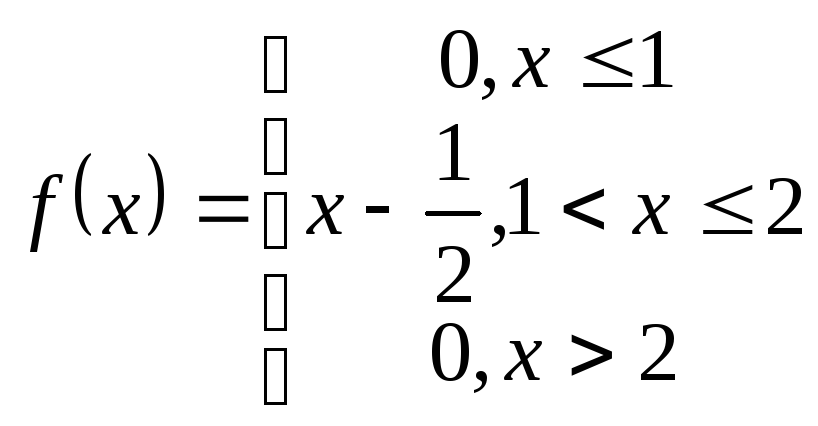
Розв’язування. Розглянемо такі випадки:

а) . При цьому;

б).Тоді;

в) . Маємо: .

Відзначимо такі властивості щільності розподілу

1. Щільність розподілу – невід’ємна функція: . Це дійсно так, оскільки – монотонна неспадна функція, а – її похідна . Графік щільності розподілу називають кривою розподілу.

2. Невласний інтеграл від щільності розподілу в межах від додорівнює одиниці:.

Дійсно, подія, яка полягає в тому, що прийме значення в інтервалі, є достовірною:.

Зауважимо, що сам термін “щільність розподілу” було введено по аналогії з щільністю маси в точці. Дійсно, оскільки , то. Отже, ймовірність того, щоприйме значення, яке належить інтервалу, наближено дорівнює добуткові щільності ймовірності в даній точці на довжину інтервалу.