
- •Расчетно-графическая работа № 2 Задача 1. Прямоугольные и полярные координаты.
- •Задача 2. Прямая линия.
- •Составить уравнение прямой, отсекающей на оси координат отрезок и образующей с положительным направлением оси абсцисс угол .
- •Задача 3. Векторы и простейшие действия над ними
- •Задача 4. Скалярное и векторное произведение. Смешанное произведение.
Расчетно-графическая работа № 2 Задача 1. Прямоугольные и полярные координаты.
-
Даны концы отрезка АВ: А (1), В (5); вне отрезка АВ расположена точка С, причем ее расстояние от точки А в три раза больше расстояния от точки В. Определить координату точки С.
-
Определить расстояние между точками М (3) и N (-5).
-
Определить расстояние между точками Р
 и Q
и Q
 .
. -
Двумя точками отрезок АВ разделили на три равные части. Определить координаты точек деления, если А (-1), В (5).
-
Даны точки А (-7), В (-3). Вне отрезка АВ расположены точки C и D, причем СА = BD =
 .
Определить координаты точек С и D.
.
Определить координаты точек С и D. -
Определить расстояние между точками А (3; 8) и В (-5, 14).
-
Показать, что треугольник АВС с вершинами А (-3; -3), В (-1; 3), С (11; -1) – прямоугольный.
-
Даны концы отрезка АВ: А (-2; 5), В (4; 17). На отрезке АВ расположена точка С, расстояние которой от точки А в два раза больше расстояния от точки В. Определить координаты точки С.
-
Серединой отрезка АВ является точка С (2; 3). Определить координаты точки А, если В (7; 5).
-
Даны вершины треугольника АВС: А
 ,
В
,
В
 ,
С
,
С
 .
Определить координаты точки пересечения
медиан треугольника.
.
Определить координаты точки пересечения
медиан треугольника. -
Определить площадь треугольника с вершинами А (-2; -4), В (2; 8), С (10; 2).
-
Построить на координатной плоскости точки А
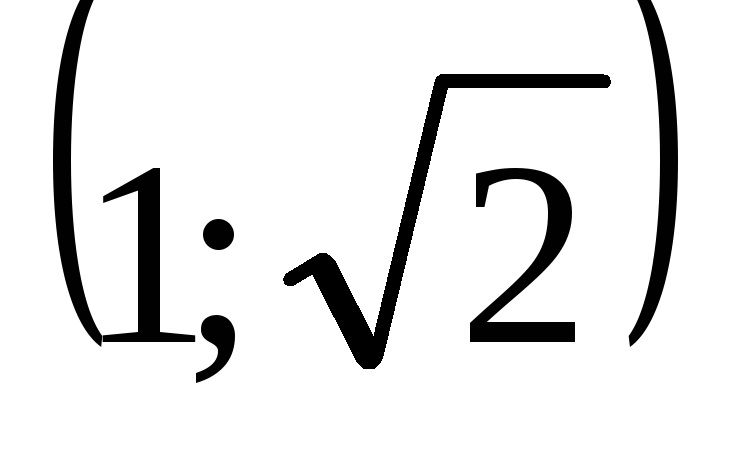 ,
В
,
В
 ,
С
,
С
 ,
D
,
D
 .
. -
Определить расстояние между точками:
а) А (2; 3) и В (-10; -2);
б) А
![]() и В
и В
![]() .
.
-
Показать, что треугольник с вершинами А (2; -1), В (4; 2), С (5; 1) – равнобедренный.
-
Даны вершины треугольника: А (-1; -1), В (0; -6) и С (-10; 2). Найти длину медианы, проведенной из вершины А.
-
Даны концы отрезка АВ: А (-3; 7) и В (5; 11). Тремя точками отрезок разделили на четыре равные части. Определить координаты точек деления.
-
Найти площадь треугольника с вершинами А (1; 5), В (2; 7), С (4; 11).
-
Даны три последовательные вершины параллелограмма: А (11; 4), В (-1; -1), С (5; 7). Определить координаты четвертой вершины.
-
Даны две вершины треугольника А (3; 8) и В (10; 2) и точка пересения медиан М (1; 1). Найти координаты третьей вершины треугольника.
-
Даны вершины треугольника: А (7; 2), В (1; 9) и С (-8; -11). Найти расстояния точки пересечения медиан от вершин треугольника.
-
Точки L (0; 0), М (3; 0) и N (0; 4) являются серединами сторон треугольника. Вычислить площадь треугольника.
-
Построить точки, заданные полярными координатами: А
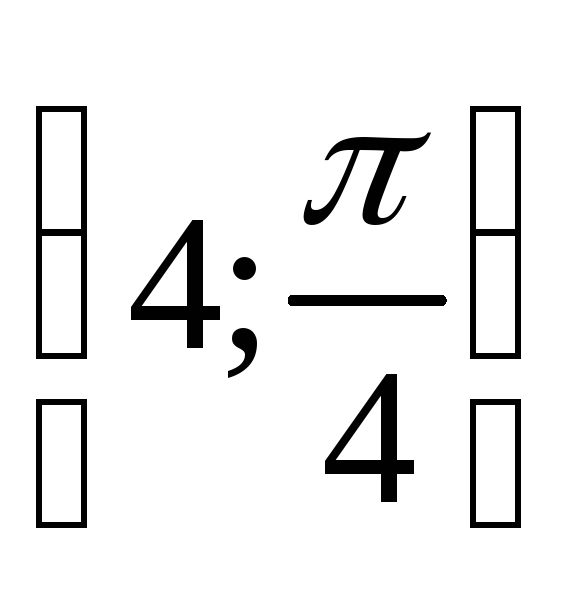 ,
В
,
В
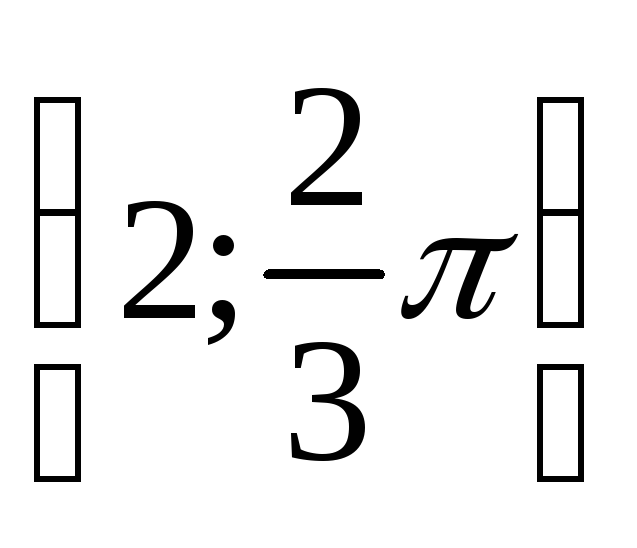 ,
С
,
С
 ,
D
,
D
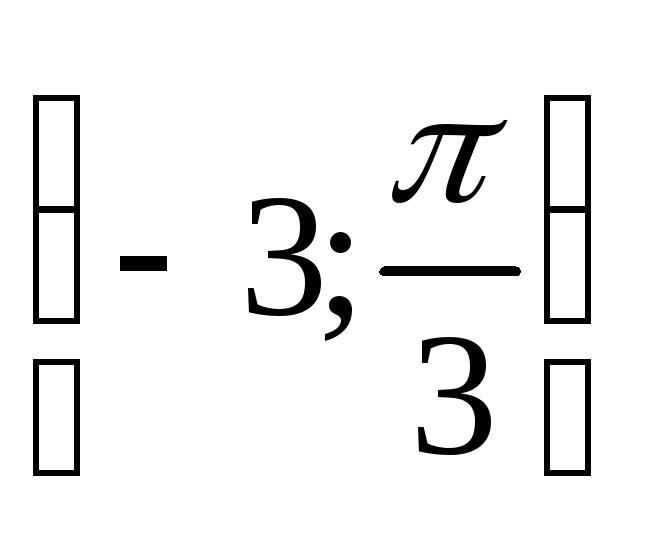 ,
E
,
E
 ,
F
,
F
 .
. -
Найти полярные координаты точки М
 ,
если полюс совпадает с началом координат,
а полярная ось – с положительным
направлением оси абсцисс.
,
если полюс совпадает с началом координат,
а полярная ось – с положительным
направлением оси абсцисс. -
Найти прямоугольные координаты точки А
 ,
определяемой полярными координатами,
если полюс совпадает с началом координат,
а полярная ось направлена по оси абсцисс.
,
определяемой полярными координатами,
если полюс совпадает с началом координат,
а полярная ось направлена по оси абсцисс. -
Построить точки А
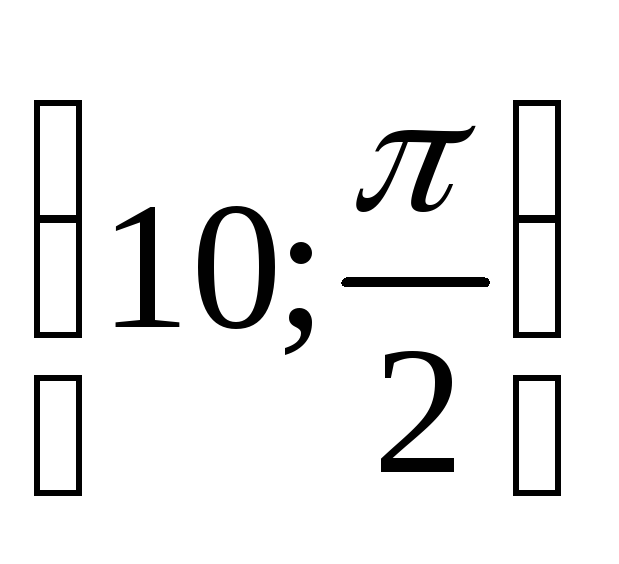 ,
В
,
В
 ,
С
,
С
 ,
D
,
D ,
E
,
E
 ,
F
,
F
 .
. -
Даны полярные координаты точки М
 .
Найти ее прямоугольные координаты,
если начало координат совпадает с
полюсом, а ось Ох – с полярной осью.
.
Найти ее прямоугольные координаты,
если начало координат совпадает с
полюсом, а ось Ох – с полярной осью. -
Даны полярные координаты точки М
 .
Найти ее декартовы координаты.
.
Найти ее декартовы координаты. -
Определить расстояние между точками М1
 и М2
и М2
 .
.
