4.5. Розв’язування транспортної задачі на мережі

Серед сучасних методів оптимізації і керування виробничими процесами значна роль належить мережевим методам. Широке коло задач математичного програмування можна подати в мережевому вигляді. Особливо це стосується транспортних задач, які мають цілком природну інтерпретацію як мережеві задачі, бо вони пов’язані з певною мережею транспортних маршрутів (доріг, залізничних, водяних шляхів, маршрутів повітряних трас, трубопроводів тощо). У цьому параграфі буде розглянуто кілька типових мережевих задач математичного програмування.

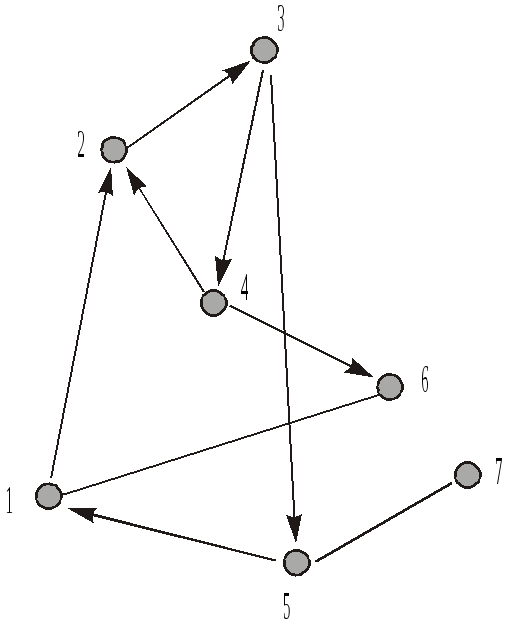
Назвемо графом будь-яку систему відрізків (прямолінійних чи криволінійних), у певний спосіб з’єднаних між собою (рис. 5.2).

Н

Рис. 5.2.

азвані відрізки, якщо їм приписано напрям, називаютьсядугами графа; надалі позначатимемо їх, наприклад:— відрізок, що з’єднує точку 1 з точкою 2 (рис. 5.2).

Точки, що є кінцями або початками дуг графів, в яких можуть з’єднуватись дві дуги або більше, називаються вершинами графа: кожна з вершин позначається певним номером (натуральним числом: 1, 2, 3, 4, ...), наприклад, точки 1, 2, 3, — вершини (рис. 5.2).

Отже, кожній дузі відповідає впорядкована пара вершин , де перший індексі означає початок дуги (вхід), другий індекс j — кінець дуги (вихід); тим самим задано орієнтацію (напрям) дуги, що геометрично зображається стрілкою в напрямі від початку до кінця дуги.

Дуги таназиваються симетричними, або взаємними, наприклад: (2, 4) і (4, 2).

Ребром(аболанкою) графа називається ненапрямлений відрізок, що зображає дугу. Позначимо ребра символами, наприклад[5, 7] — ребро; тоді як для відповідних дуг ця рівність не справджується:.

Мережею (або сіттю) називається граф, елементам якого (дугам, вершинам, деяким їх сукупностям) поставлені у відповідність деякі параметри, що визначають їх властивості.

Такими параметрами можуть бути, наприклад, пропускні здатності шляхів, величини запасів чи потреб у певних пунктах — вершинах графа тощо.

Шляхому графі називається послідовність дуг, кінець кожної з яких збігається з початком наступної, крім останньої (або початок кожної з яких збігається з кінцем попередньої, крім першої), тобто...,.

Шлях зручно позначати послідовністю вершин, через які він проходить, тобто . Прикладом шляху є послідовність таких дуг (1, 2), (2, 3), (3, 5) або (1,2, 3, 5).

Контуром називається шлях, початкова вершина якого збігається з кінцевою, наприклад (1, 2), (2, 3), (3, 5), (5, 1) = (1, 2, 3, 5, 1).

Граф називається сильно (чи міцно) зв’язаним, якщо будь-які його вершини і і j можна з’єднати шляхом, що йде з і в j.

Якщо в означеннях шляху, контуру і сильної зв’язаності графа поняття дуги замінити поняттям ребра, то дістанемо означення ланцюга, циклу і зв’язаності графа.

Легко збагнути, що ребра дуг, які утворюють шлях і контур, завжди утворюють відповідно ланцюг і цикл, проте зворотне твердження не справджується. Це саме стосується і зв’язаності: зв’язаний граф не обов’язково буде міцно зв’язаним.

Ланцюг і циклпозначають аналогічно до шляху і контуру, проте замість круглих використовують квадратні дужки, наприклад, ланцюг [1, 2], [2, 3], [3, 4], [4, 6], або [1, 2, 3, 4, 6]; цикл [1, 2], [2, 3], [3, 4], [4, 6], [6, 1], або [1, 2, 3, 4, 6, 1]; відповідні послідовності дуг не завжди є шляхами чи контурами.

Деревомназивається граф, який не має циклів і в якому кожна вершина зв’язана з будь-якою іншою деяким ланцюгом ребер.

4.5.1. Транспортна задача у мережевій формі

Нехай задано граф із скінченною кількістю вершин і ребер. Поставимо у відповідність кожній вершині деяке число (і = 1, 2, ..., m), яке назвемо інтенсивністю i-ої вершини, а кожній дузі (іj) — число — пропускну здатність (іj)-ої дуги, відносячи ці величини до певного відрізка часу t (0 < t < ), наприклад, до певної одиниці часу. За цих умов скінченний граф перетворюється в мережу (сіть). Позначимо черезневідому величину, що означає обсяг деякої продукції, яку переміщають по (ij)-й дузі за деякий відрізок часу. Тоді для цього самого відрізка часу для кожної k-ої вершини графа можна записати таку балансову рівність:

. (5.42)

Справді, перша сума означає сумарний обсяг певної продукції, що протягом означеного часу прибуває в k-ту вершину по дугах, а друга сума означає сумарний обсяг цієї продукції, що вибуває подугах зk-ої вершини за той самий час. Отже, є обсягом розглядуваної продукції, який споживається (акумулюється) вk-ій вершині, а є обсягом цієї продукції, який виділяється (продукується) вершиною за згаданий відрізок часу. Вершину, для якої, називатимемостоком, а вершину, для якої —джерелом. Вершини, в яких , назвемонейтральними.

Природно вважати змінні іневід’ємними і обмеженими зверху числамиі, так що:

. (5.43)

У свою чергу, можна вважати, що величини іможуть змінюватися в таких межах:

. (5.44)

Рівняння (5.42) можна трактувати як рівняння безперервності потоку розглядуваної продукції по певній мережі (доріг, трубопроводів і т. п.) в деякому околі k-ої вершини (пункту). Прикладом може бути рівняння збереження кількості рідини, що проходить по трубопровідній мережі.

Можна поставити вимогу, щоб за заданих величин інтенсивностей джерел та стоків і величин пропускних здатностей дугзнайдені значення невідомихзадовольняли деякий критерій оптимальності, наприклад, надавали мінімального значення лінійній функції:

. (5.45)

Легко помітити, що сформульована сітьова транспортна задача (5.42)—(5.45) є узагальненням звичайної транспортної задачі (5.1)—(5.4) за умови наявності проміжних пунктів перевезень і обмежених пропускних здатностей шляхів сполучення.