- •Раздел I гидромеханические процессы
- •Основы гидравлики
- •Основные свойства жидкостей в гидравлике
- •Элементы гидростатики
- •Уравнения гидростатического равновесия
- •Давление жидкости на дно и стенки сосуда
- •Практическое использование законов гидростатики
- •Элементы гидродинамики
- •Основные понятия и определения
- •Уравнения динамического равновесия жидкости
- •Основные уравнения гидравлики
- •Уравнение неразрывности или сплошности потока
- •Уравнение Бернулли
- •Теория движения жидкости по трубам
- •Распределение скоростей по сечению трубопровода
- •Сопротивления в трубопроводах
- •Гидродинамическое подобие
- •Движение твердых тел в жидкости (газе)
- •Движение жидкости (газа) через слои пористых и зернистых твердых материалов
- •Движение жидкости через неподвижный слой
- •Движение жидкости через псевдоожиженный слой
- •Перемещение жидкостей. Насосы
- •Общие сведения
- •Основные характеристики насосов
- •Объемные насосы
- •Лопастные насосы
- •Струйные насосы
- •Пневматические насосы
- •Сжатие и разрежение газов
- •Общие сведения
- •Термодинамические основы процесса сжатия газов
- •Поршневые компрессионные машины
- •Установка поршневых компрессоров и вакуум-насосов
- •Центробежные и осевые компрессионные машины
- •Роторные компрессионные машины
- •Струйные компрессионные машины
- •Разделение неоднородных систем
- •Характеристика неоднородных систем и методов их разделения
- •Материальный баланс процесса разделения
- •Разделение неоднородных систем осаждением
- •Отстаивание
- •Устройство отстойников
- •Расчёт отстойников
- •Осаждение под действием центробежной силы
- •Мокрая очистка газов
- •Осаждение под действием электрического поля
- •Устройство и расчёт электрофильтров
- •Фильтрование
- •Скорость фильтрования
- •Фильтровальные перегородки
- •Перемешивание в жидких средах
- •Общие сведения
- •Степень перемешивания
- •Интенсивность перемешивания
- •Эффективность перемешивания
- •Механическое перемешивание
- •Мощность, потребляемая механическими мешалками
- •Сравнительная характеристика и область применения механических мешалок
Сжатие и разрежение газов
Общие сведения
В производственных процессах, связанных с использованием газов (диспергирование, перемешивание, пневмотранспорт, сушка, абсорбция и т. д.), перемещение и сжатие последних происходит за счет энергии, сообщаемой им машинами, которые носят общее название компрессионных. При этом производительность компрессионных установок может достигать десятков тысяч кубометров в час, а давление изменяется в пределах 10–8–103атм., что обусловливаетбольшое разнообразие типов и конструкций машин, применяемых для перемещения, сжатия и разрежения газов. Машины, предназначенные для создания повышенныхдавлений, получили название компрессоров, а машины, работающие на создание разрежения –вакуум-насосов.
Классифицируют компрессионные машины в основном по двум признакам: принципу действия и степени сжатия. Степень сжатия– это отношение конечного давления газа на выходе из машиныр2к начальному давлению на входеp1(т. е.p2/p1).
По принципу действия компрессионные машины подразделяют на поршневые, лопастные (центробежные и осевые), ротационные и струйные.
По степени сжатия различают:
– компрессоры, используемые для создания высоких давлений, со степенью сжатия р2/р1> 3;
– газодувки, служащие для перемещения газов при большом сопротивлении газопроводной сети, при этом 3 > p2/p1>1,15;
– вентиляторы, применяемые для перемещения больших количеств газа при p2/p1< 1,15;
– вакуум-насосы, отсасывающие газ из пространства с пониженным давлением (ниже атмосферного) и нагнетающие его в пространство с повышенным (выше атмосферного) или атмосферным давлением.
В качестве вакуум-насосов могут быть использованы любые компрессионные машины; более глубокий вакуум создают поршневые и ротационные машины.
В отличие от капельных жидкостей, физические свойства газов функционально зависят от температуры и давления; процессы перемещения и сжатия газов связаны с внутренними термодинамическими процессами. При малых перепадах давлений и температур изменения физических свойств газов в процессе их движения с малыми скоростями и давлениями, близкими к атмосферному, незначительны. Это дает возможность использования всех основных положений и законов гидравлики для их описания. Однако при отклонении от нормальных условий, в особенности при высоких степенях сжатия газа, многие положения гидравлики претерпевают изменение.
Термодинамические основы процесса сжатия газов
Влияние температуры на изменение объема газа при постоянном давлении, как известно, определяется законом Гей – Люссака, т. е. при p = const объем газа прямо пропорционален его температуре:
![]() ,
,
где V1иV2– объемы газа соответственно при температурахТ1иТ2, выраженные по шкале Кельвина.
Связь между объемами газа при разных температурах может быть представлена зависимостью
![]() , (4.1)
, (4.1)
где VиV0– конечный и начальный объемы газа, м3;t иt0– конечная и начальная температура газа, °С;βt– относительный коэффициент объемного расширения, град.–1.
Изменение давления газа в зависимости от температуры:
![]() , (4.2)
, (4.2)
где рир0– конечное и начальное давление газа, Па;βр– относительный температурный коэффициент давления, град.–1.
Масса газа Мпри
изменении его объема остается постоянной.
Если ρ1иρ2плотности двух температурных состояний
газа, то![]() и
и![]() либо
либо![]() ,
т.е. плотность газа при постоянном
давлении обратно пропорциональна его
абсолютной температуре.
,
т.е. плотность газа при постоянном
давлении обратно пропорциональна его
абсолютной температуре.
По закону Бойля-Мариотта, при одной и
той же температуре произведение удельного
объема газа vна значение его давленияр есть величина постояннаяpv = const.
Следовательно, при постоянной температуре![]() ,
а
,
а![]() ,
т. е. плотность газа прямо пропорциональна
давлению, так как
,
т. е. плотность газа прямо пропорциональна
давлению, так как![]() .
.
Учитывая уравнение Гей-Люссака, можно получить соотношение, связывающее три параметра газа: давление, удельный объем и его абсолютную температуру:
![]() . (4.3)
. (4.3)
Последнее уравнение носит название уравнения Клайперона. В общем виде:
![]() либо
либо![]() , (4.4)
, (4.4)
где R– газовая постоянная, которая представляет собой работу, совершаемую единицей массы идеального газа в изобарном (p = const) процессе; при изменении температуры на 1° газовая постояннаяRимеет размерность Дж/(кгград):
![]() , (4.5)
, (4.5)
где lр– удельная работа изменения объема, совершаемого 1 кг идеального газа при постоянном давлении, Дж/кг.
Таким образом, уравнение (4.4) характеризует состояние идеального газа. При давлении газа свыше 10 атм использование этого выражения вносит погрешность в расчеты (pv ≠RT), поэтому рекомендуется пользоваться формулами, которые более точно описывают зависимость между давлением, объемом и температурой реального газа. Например, уравнением Ван-дер-Ваальса:
![]() , (4.6)
, (4.6)
где R = 8314/M– газовая постоянная, Дж/(кг·К);М– молекулярная масса газа, кг/кмоль;аив – величины, постоянные для данного газа.
Величины аивмогут быть рассчитаны по критическим параметрам газа (Ткриркр):
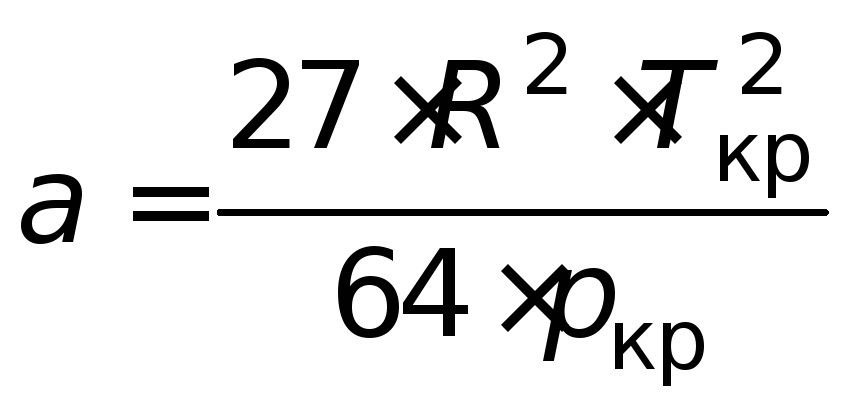 ;
;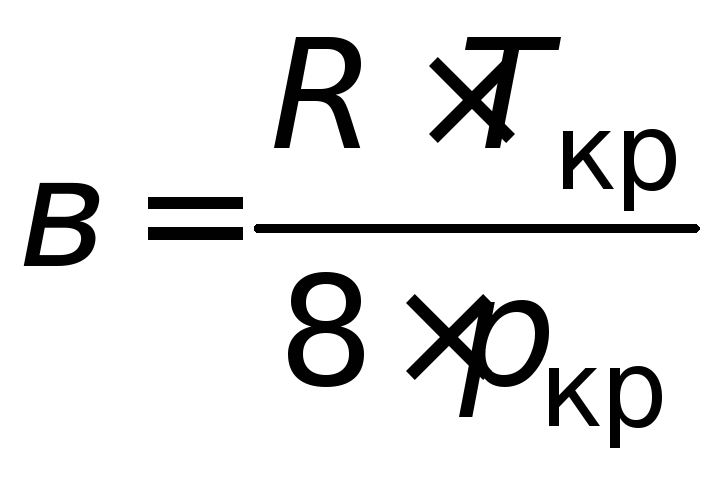 . (4.7)
. (4.7)
При высоких давлениях величина а/v2(дополнительного давления в уравнении Ван-дер-Ваальса) мала по сравнению с давлениемp и ею можно пренебречь, тогда уравнение (4.6) превращается в уравнение состояния реального газа Дюпре:
![]() , (4.8)
, (4.8)
где величина в зависит только от рода газа и не зависит от температуры и давления.
На практике для определения параметров газа при различных его состояниях чаще пользуются термодинамическими диаграммами: Т–S(температура–энтропия),p–i(зависимость давления от энтальпии),p–V(зависимость давления от объема).
Рисунок
4.1 – Т–Sдиаграмма
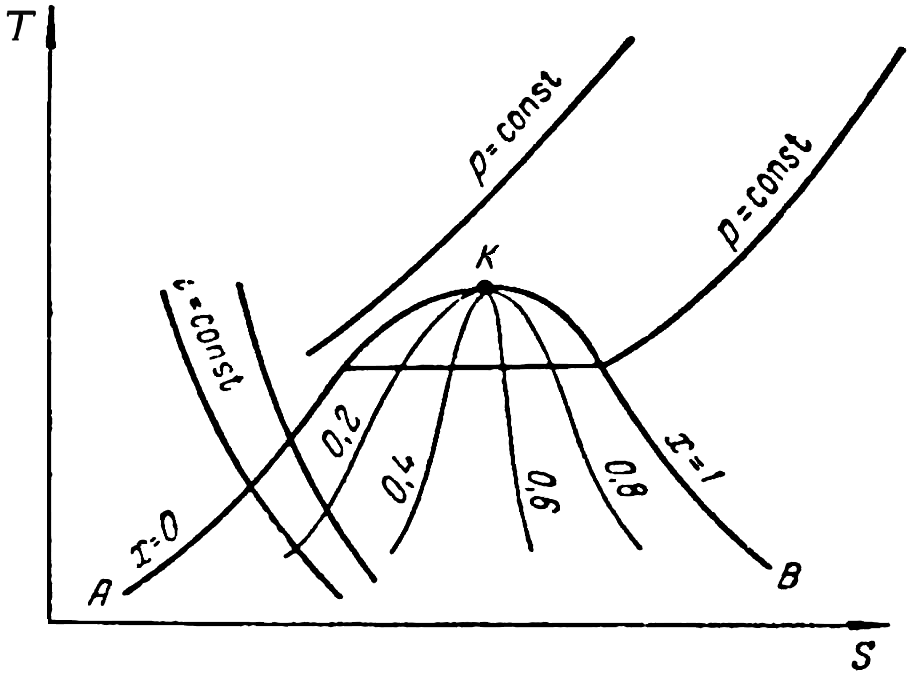
Все параметры газа на диаграмме Т–Sотнесены к 1 кг газа.
Так как в соответствии с термодинамическим
определением
![]() ,
то теплота изменения состояния газа
,
то теплота изменения состояния газа![]() .
Следовательно, площадь под кривой,
описывающей изменение состояния газа,
численно равна энергии (теплоте) изменения
состояния.
.
Следовательно, площадь под кривой,
описывающей изменение состояния газа,
численно равна энергии (теплоте) изменения
состояния.
Процесс изменения параметров газа называют процессом изменения его состояния. Каждое состояние газа характеризуется параметрами p,vиТ. В процессе изменения состояния газа могут меняться все параметры или один из них оставаться постоянным. Так, протекающий при постоянном объеме процесс называетсяизохорическим, при постоянном давлении –изобарическим, а при постоянной температуре –изотермическим.Когда при отсутствии теплообмена между газом и внешней средой (теплота не отводится и не подводится) изменяются все три параметра газа (p,v,Т) в процессе его расширения либо сжатия, процесс называется адиабатическим, а когда изменение параметров газа происходит при непрерывном подводе или отводе теплоты–политропическим.
При изменяющихся давлении и объеме, в зависимости от характера теплообмена с окружающей средой, изменение состояния газа в компрессионных машинах может происходить изотермически, адиабатически и политропически.
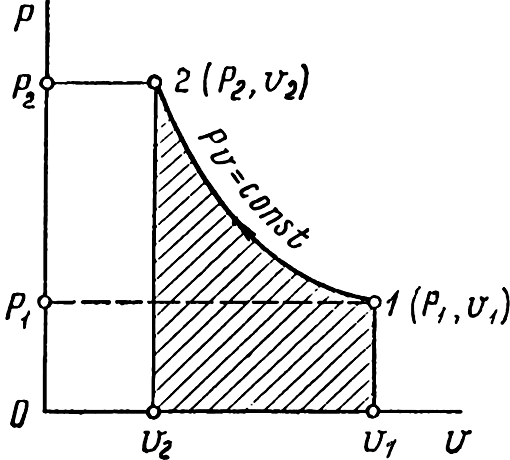
При изотермическом процессе изменение состояния газа следует закону Бойля–Мариотта:
pv = const.
На диаграмме p–vэтот процесс
изображается гиперболой (рис. 4.2).
Работа 1 кг газаlграфически
представляется заштрихованной площадью,
которая равна![]() ,
т. е.
,
т. е.
![]() либо
либо![]() . (4.9)
. (4.9)
Количество тепла, которое выделяется при изотермическом сжатии 1 кг газа и которое необходимо отводить путем охлаждения, чтобы температура газа оставалась постоянной:
![]() , (4.10)
, (4.10)
где cvиcр– удельные теплоемкости газа при постоянном объеме и давлении, соответственно.
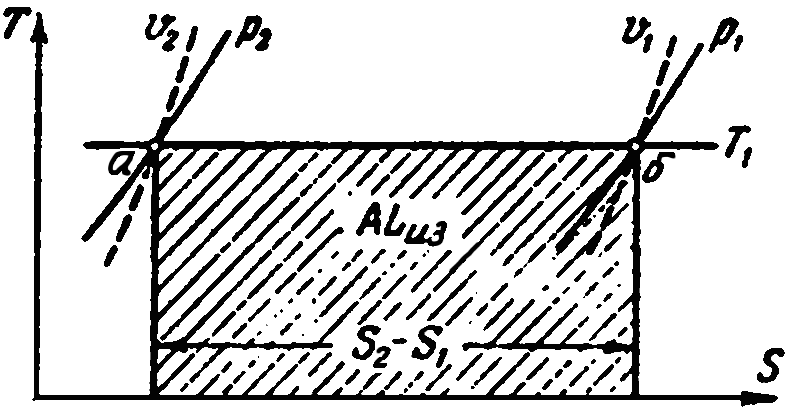
На диаграмме Т–Sпроцесс изотермического сжатия газа от давленияр1до давленияр2изображается прямой линиейаб, проведенной между изобарамир1 ир2(рис. 4.3).
|
|
|
|
Рисунок
4.2 – Процесс изотермического сжатия
газа на диаграмме
|
Рисунок 4.3 – Процесс изотермического сжатия газа на диаграмме Т–S |
Тепло, эквивалентное работе сжатия, изображается площадью, ограниченной крайними ординатами и прямой аб, т. е.
![]() .
(4.11)
.
(4.11)
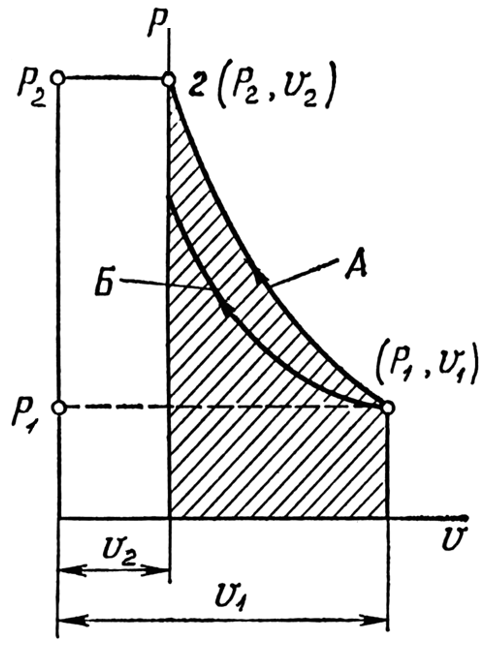
Рисунок
4.4 – Процессы
сжатия газа на диаграмме
А
– адиабатический процесс;
Б
– изотермический процесс
![]() :
:
При адиабатическом процессе сжатия газа изменение его состояния происходит за счет изменения его внутренней энергии, а следовательно, и температуры.
В общей форме уравнение адиабатического процесса описывается выражением:
![]() ,
(4.12)
,
(4.12)
где
![]() –
показатель адиабаты.
–
показатель адиабаты.
Графически (рис. 4.4) этот процесс на диаграмме p–vизобразится гиперболой более крутой, чем на рис. 4.2., так какk > 1.
Если принять
![]() ,
то
,
то![]() .
(4.13)
.
(4.13)
Поскольку
![]() иR= const, полученное уравнение можно
выразить иначе:
иR= const, полученное уравнение можно
выразить иначе:
 или
или![]() .
(4.14)
.
(4.14)
Путем соответствующих преобразований можно получить зависимости для других параметров газа:
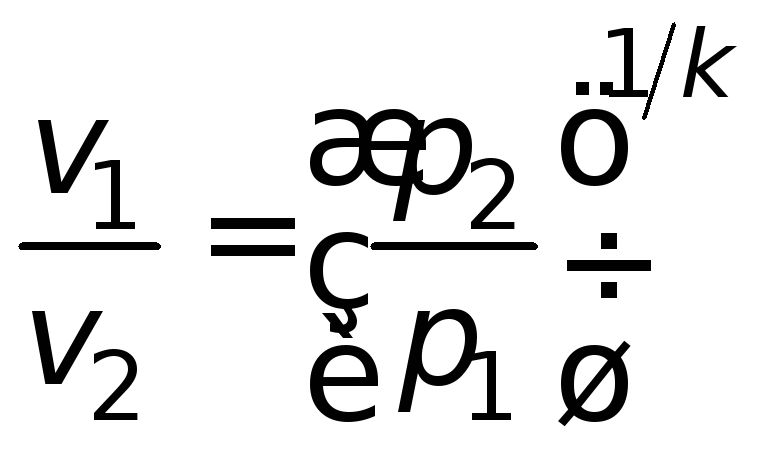 ;
;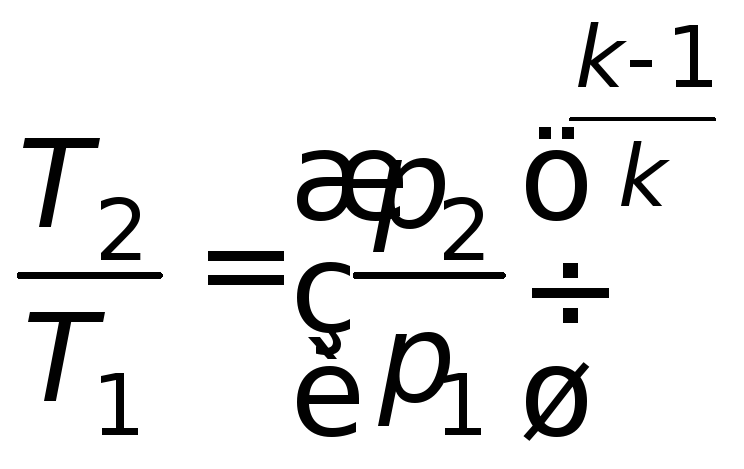 . (4.15)
. (4.15)
Таким образом, температура газа в конце его адиабатического сжатия
 . (4.16)
. (4.16)
Работа, совершаемая 1 кг газа в условиях адиабатического процесса:
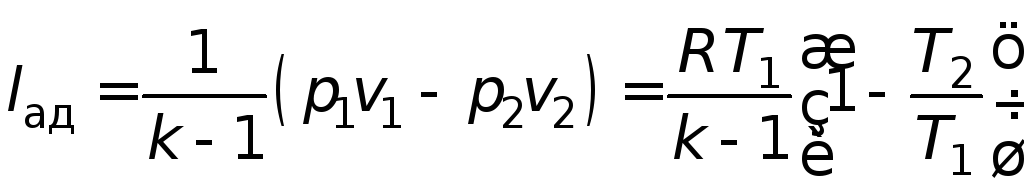 . (4.17)
. (4.17)
Тепло, выделяющееся при адиабатическом сжатии газа, эквивалентно затрачиваемой работе:
![]() . (4.18)
. (4.18)
С учетом соотношений (4.15) работа на сжатие газа при адиабатическом процессе
 . (4.19)
. (4.19)
Процесс адиабатического сжатия характеризуется полным отсутствием теплообмена между газом и окружающей средой, т.е. dQ = 0, аdS = dQ/T, поэтомуdS = 0.
Таким образом, процесс адиабатического сжатия газа протекает при постоянной энтропии (S= const). На диаграммеТ–Sэтот процесс изобразится прямой линиейАВ(рис. 4.5).
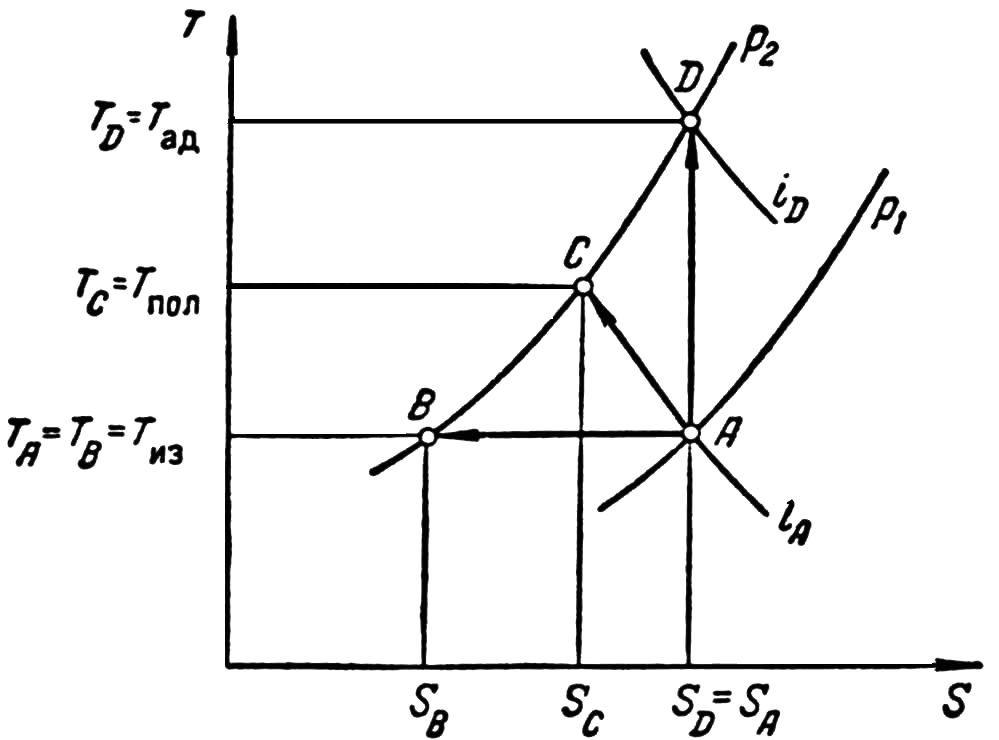
Рисунок 4.5 – Изображение процессов сжатия газа на диаграмме Т–S
Если в процессе сжатия выделяющееся тепло отнимается в меньшем количестве, чем это необходимо для изотермического процесса (что происходит во всех реальных процессах сжатия), то фактически затрачиваемая работа будет большей, чем при изотермическом сжатии, и меньшей, чем при адиабатическом:
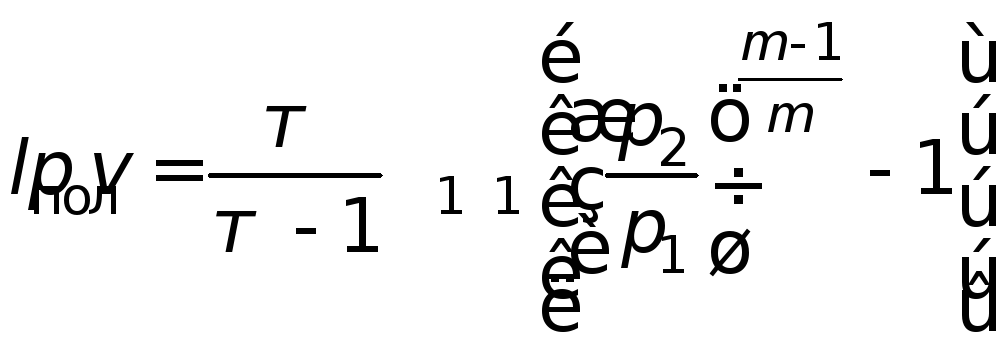 , (4.20)
, (4.20)
где m– показатель политропы,k>m>1
(для воздухаm![]() ).
).
Значение показателя политропы mзависит от природы газа и условий теплообмена с окружающей средой. В компрессионных машинах без охлаждения показатель политропы может быть больше показателя адиабаты (m >k), т. е. процесс в этом случае протекает по сверхадиабате.
Работу, затрачиваемую на разрежение газов, рассчитывают по тем же уравнениям, что и работу на сжатие газов. Отличие лишь в том, что р1 будет меньше атмосферного давления.
Процесс политропического сжатиягаза от давленияр1 до давления р2 на рис. 4.5 изобразится прямойАС. Количество тепла, выделяемое при политропическом сжатии 1 кг газа, численно равно удельной работе сжатия:
![]() . (4.21)
. (4.21)
Конечная температура сжатия газа
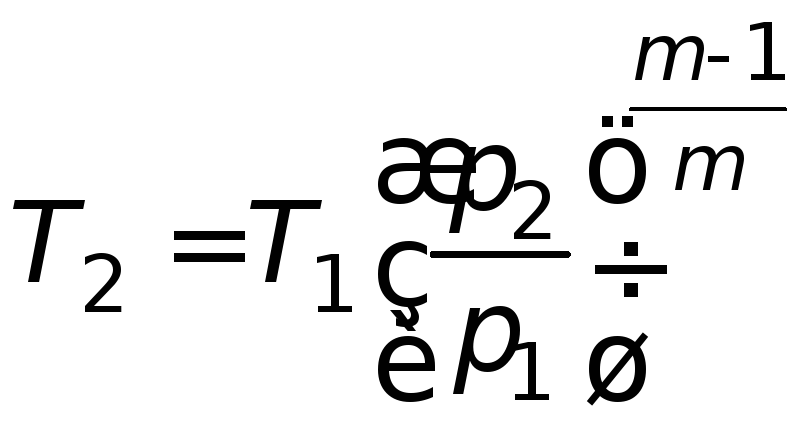 . (4.22)
. (4.22)
Мощность,затрачиваемая компрессионными машинами на сжатие и разрежение газов, зависит от их производительности, конструктивных особенностей, теплообмена с окружающей средой.
Теоретическая мощность, затрачиваемая
на сжатие газа
![]() ,
определяется производительностью и
удельной работой сжатия:
,
определяется производительностью и
удельной работой сжатия:
![]() , (4.23)
, (4.23)
где GиV– массовая и объемная
производительность машины соответственно;![]() –
плотность газа.
–
плотность газа.
Следовательно, для различных процессов сжатия теоретически затрачиваемая мощность:
![]() ;
(4.24)
;
(4.24)
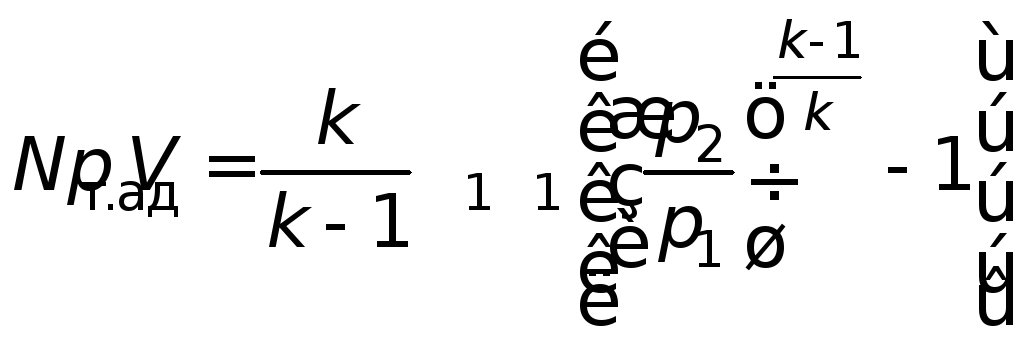 ; (4.25)
; (4.25)
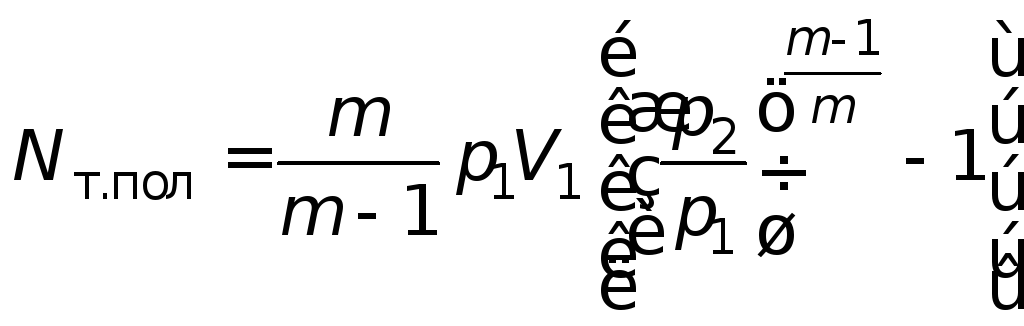 , (4.26)
, (4.26)
где
![]() –
объемная производительность компрессионной
машины, приведенная к условиям всасывания.
–
объемная производительность компрессионной
машины, приведенная к условиям всасывания.
Фактически затрачиваемая мощность в силу ряда причин больше, т.е. потребляемая машиной энергия выше, чем та, которую она передает газу.
Для оценки эффективности компрессионных машин используют сравнение данной машины с наиболее экономичной машиной того же класса.
Машины с охлаждением сравнивают с машинами, которые сжимали бы газ при данных условиях изотермически. В этом случае к. п. д. носит название изотермического, из:
![]() , (4.27)
, (4.27)
где N– фактически затрачиваемая мощность данной машиной.
Если машины работают без охлаждения, то сжатие газа в них происходит по политропе, показатель которой выше показателя адиабаты (m k). Поэтому затрачиваемую мощность в таких машинах сравнивают с мощностью, которую затрачивала бы машина при адиабатическом сжатии газа. Отношение этих мощностей представляет собой адиабатический к.п.д.:
![]() .
(4.28)
.
(4.28)
С учетом мощности, теряемой на механическое трение в машине и учитываемой механическим к.п.д. – мех, мощность на валу компрессионной машины:
![]() либо
либо![]() . (4.29)
. (4.29)
Мощность двигателя рассчитывается с учетом к.п.д. самого двигателя и к.п.д. передачи:
![]() . (4.30)
. (4.30)
Установочная мощность двигателя
принимается с запасом (![]() ):
):
![]() . (4.31)
. (4.31)
Значение адколеблется в пределах 0,930,97;изв зависимости от степени сжатия имеет значение 0,640,78; механический к. п. д. меняется в пределах 0,850,95.