spz / lect / lekc2_2_TI

Таблиці ідентифікаторів. Організація таблиць ідентифікаторів

1.Призначення та особливості побудови таблиць ідентифікаторів.

2.Найпростіші методики побудови таблиць ідентифікаторів.

3.Побудова таблиць ідентифікаторів методом бінарного дерева

Призначення йособливості побудовитаблиць ідентифікаторів

Перевірка правильності семантики і генерація коду вимагають знання характеристик змінних, констант, функцій і інших елементів, що зустрічаються у програмі вхідною мовою. Усі ці елементи у вхідній програмі, як правило, позначаються ідентифікаторами. Виділення ідентифікаторів і інших елементів вхідної програми відбувається на фазі лексичного аналізу. Їхні характеристики визначаються на фазах синтаксичного розбору, семантичного аналізу і підготовки до генерації коду. Склад можливих характеристик і методи їх визначення залежать від семантики вхідної мови.

У будь-якому випадку компілятор повинний мати можливість зберігати всі знайдені ідентифікатори і зв'язані з ними характеристики на протязі всього процесу компіляції, щоб мати можливість використовувати їх на різних фазах компіляції.

Для цієї мети, як було сказано вище, у компіляторах використовуються спеціальні сховища даних, називані таблицями символів або таблицями ідентифікаторів.

Будь-яка таблиця ідентифікаторів складається з набору полів, кількість яких дорівнює числу різних ідентифікаторів, знайдених у вхідній програмі. Кожне поле містить у собі повну інформацію про даний елемент таблиці. Компілятор може працювати з однією або декількома таблицям ідентифікаторів — їхня кількість залежить від реалізації компілятора. Наприклад, можна організовувати різні таблиці ідентифікаторів для різних модулів вхідної програми або для різних типів елементів вхідної мови.

Склад інформації, збереженої в таблиці ідентифікаторів для кожного елемента вхідної програми, залежить від семантики вхідної мови і типу елемента. Наприклад, у таблицях ідентифікаторів може зберігатися наступна інформація:

для змінних:

-ім'я змінної;

-тип даних змінною;

-область пам'яті, зв'язана із змінною;

для констант:

-назва константи (якщо воно є);

-значення константи;

-тип даних константи (якщо потрібно);

для функцій:

-ім'я функції;

-кількість і типи формальних аргументів функції;

-тип результату, що повертається;

-адреса коду функції.

Приведений вище склад збереженої інформації є приблизним і приводиться як зразок. Конкретне наповнення таблиць ідентифікаторів залежить від реалізації компілятора. Крім того, не вся інформація, збережена в таблиці ідентифікаторів, заповнюється компілятором відразу — він може декілька разів виконувати звертання до даних і таблиці ідентифікаторів на різних фазах компіляції. Наприклад, імена змінних можуть бути виділені на фазі лексичного аналізу, типи даних для змінних — на фазі синтаксичного розбору, а область пам'яті зв'язується із змінною тільки на фазі підготовки до генерації коду.

Поза залежністю від реалізації компілятора принцип його роботи з таблицею ідентифікаторів залишається тим самим — на різних фазах компіляції компілятор змушений багаторазово звертатися до таблиці для пошуку інформації і запису нових даних. Як правило, кожен елемент у вхідній програмі однозначно ідентифікується своїм іменем. Тому компілятору часто приходиться виконувати пошук необхідного елемента в таблиці ідентифікаторів по його імені, у той час як процес заповнення таблиці виконуються нечасто – нові ідентифікатори описуються в програмі набагато рідше, ніж використовуються. Звідси можна зробити висновок, що таблиці ідентифікаторів повинні бути організовані таким чином, щоб компілятор мав можливість максимально швидкого пошуку потрібного йому елемента.

Найпростіші методи побудови таблиць ідентифікаторів

Найпростіший спосіб організації таблиці полягає в тому, щоб додавати елементи в порядку їх надходження. Тоді таблиця ідентифікаторів буде представляти невпорядкований масив інформації, кожна комірка якого буде містити даніпро відповідний елементітаблиці.

Пошук потрібного елемента в таблиці буде в цьому випадку полягати в послідовному порівнянні шуканого елемента з кожним елементом таблиці, поки не буде знайдений придатний. Тоді, якщо за одиницю прийняти час, затрачуваний компілятором на порівняння двох елементів (як правило, це порівняння рядків), то для таблиці, що містить N елементів, у середньому буде виконане N/2 порівнянь.

Заповнення такої таблиці буде відбуватися елементарно просто — додаванням нового елемента в її кінець, і час, необхідний на додавання елемента (Тз), не буде залежати від числа елементів у таблиці N. Але якщо N дуже велике, то пошук зажадає значних витрат часу. Час пошуку (Тn) у такій таблиці можна оцінити як Тn = O(N). Оскільки пошук у таблиці ідентифікаторів є найчастіше виконуваною компілятором операцією, а кількість різних ідентифікаторів навіть у реальній вхідній програмі досить велике (від декількох сотень до декількох тисяч елементів), то такий спосіб організації таблиць ідентифікаторів є неефективним.

Пошук може бути виконаний більш ефективно, якщо елементи таблиці упорядковані (відсортовані) відповідно до деякого природного порядку. У нашому випадку, коли пошук буде здійснюватися по імені ідентифікатора, найбільш природно розташувати елементи таблиці в прямому чи зворотному алфавітному порядку. Ефективним методом пошуку в упорядкованому списку з N елементів є бінарний або логарифмічний пошук. Символ, який варто знайти, порівнюється з елементом (N+l)/2 у середині таблиці. Якщо цей елемент не є шуканим, то ми повинні переглянути тільки блок елементів, пронумерованих від 1 до (N+l)/2-l, чи блок елементів від (N+l)/2+1 до N у залежності від того, менше чи більше шуканий елемент від того, з яким його порівняли. Потім процес повторюється над потрібним блоком у два рази меншого розміру. Так продовжується доти, поки або елемент не буде знайдений, або алгоритм не дійде до чергового блоку, що містить один чи два елементи (з якими уже можна виконати пряме порівняння шуканого елемента).

Тому що на кожнім кроці число елементів, що можуть містити шуканий елемент,скорочується наполовину, томаксимальне число порівняньдорівнює

l+log2(N)

Тоді час пошуку елемента в таблиці ідентифікаторів можна оцінити як

Тn = O(log2N).

Наприклад: при N=128 бінарний пошук вимагає якнайбільше 8 порівнянь, а пошук у неупорядкованій таблиці – у середньому – 64 порівняння.

Метод називають “бінарним пошуком”, оскільки на кожнім кроці обсяг розглянутої інформації скорочується в два рази, “логарифмічним”, оскільки час, затрачуваний на пошук потрібного елемента в масиві, має логарифмічну залежність від загальної кількості елементом у ньому.

Недоліком методу є вимога впорядкування таблиці ідентифікаторів. Тому що масив інформації, у якому виконується пошук, повинний бути упорядкований, то час його заповнення вже буде залежати від числа елементів у масиві. Таблиця ідентифікаторів найчастіше проглядається ще до того, як вона заповнена цілком, тому потрібно, щоб умова упорядкованості виконувалося на всіх етапах звертання до неї. Отже, для побудови таблиці можна користуватися тільки алгоритмом прямого впорядкованого включення елементів.

При додаванні кожного нового елемента в таблицю спочатку треба визначити місце, куди помістити новий елемент, а потім виконати перенос частини інформації в таблиці, якщо елемент додається не в її кінець. Якщо користуватися стандартними алгоритмами, застосовуваними для організації впорядкованих масивів даних, а пошук місця включення вести за допомогою алгоритму бінарного пошуку, то середній час, необхідний на розміщення всіх елементів у таблицю, можна оцінити в такий спосіб:

Т3 = O(N*log2 N) + k*O(N2).

Тут k — деякий коефіцієнт, що відображає співвідношення між часом, затрачуваними комп'ютером на виконання операції порівняння й часом операції перенесення даних.

Таким чином, при організації логарифмічного пошуку в таблиці ідентифікаторів ми отримуємо істотне скорочення часу пошуку потрібного елемента за рахунок збільшення часу на розміщення нового елемента в таблицю. Оскільки додавання нових елементів у таблицю ідентифікаторів відбувається істотно рідше1 , ніж звертання до них, то цей метод варто визнати більш ефективним, чим метод організації невпорядкованої таблиці.

Побудова таблиць ідентифікаторів по методу бінарного дерева

Можна скоротити час пошуку шуканого елемента в таблиці ідентифікаторів, не збільшуючи значно час, необхідний на її заповнення. Для цього треба відмовитися від організації таблиці у виді безперервного масиву даних.

Існує метод побудови таблиць, при якому таблиця має форму бінарного дерева. Кожен вузол дерева являє собою елемент таблиці, причому кореневий вузол є першим елементом, зустрінутим при заповненні таблиці. Дерево називається бінарним, тому що кожна вершина в ньому може мати не більш двох віток (і, отже, не більш двох нижче лежачих вершин ). Для визначеності будемо називати дві вітки «права» і «ліва».

Розглянемо алгоритм заповнення бінарного дерева. Будемо вважати, що алгоритм працює з потоком вхідних даних, що містять ідентифікатори (у компіляторі цей потік даних породжується в процесі розбору тексту і програми).

Перший ідентифікатор, як уже було сказано, міститься у вершину дерева. Усі подальші ідентифікатори попадають у дерево по наступному алгоритму.

Крок І. Вибрати черговий ідентифікатор із вхідного потоку даних.. Якщо чергового ідентифікатора не має, та побудова дерева закінчена.

Крок 2. Зробити поточним вузлом дерева кореневу вершину.

Крок 3. Порівняти черговий ідентифікатор з ідентифікатором, що міститься в поточному вузлі дерева.

Крок 4. Якщо черговий ідентифікатор менше, то перейти до кроку 5, якщо дорівнює - повідомити про помилку і припинити виконання алгоритму (двох однакових ідентифікаторів бути не може!), інакше — перейти до кроку 7.

1 Какминимумпридобавленииновогоидентификаторавтаблицукомпилятордолженпроверить,существуетилинеттам такойидентификатор,таккаквбольшинствеязыковпрограммирования ниодинидентификатор неможет быть описан болееодногоразаСледовательно, каждая операциядобавления новогоэлементавлечет,какправило;неменееодной операциипоиска

Крок 5. Якщо у поточного вузла існує ліва вершина, то зробити її поточним вузлом і повернутися до кроку 3, інакше — перейти до кроку 6.

Крок 6. Створити нову вершину, помістити в неї черговий ідентифікатор, зробити цю нову вершину лівою вершиною поточного вузла і повернутися до кроку 1.

Крок 7. Якщо у поточного вузла існує права вершина, то зробити її поточним вузлом і повернутися до кроку 3, інакше — перейти до кроку 8.

Крок 8. Створити нову вершину, помістити в неї черговий ідентифікатор, зробити цю нову вершину правою вершиною поточного вузла і повернутися до кроку 1.

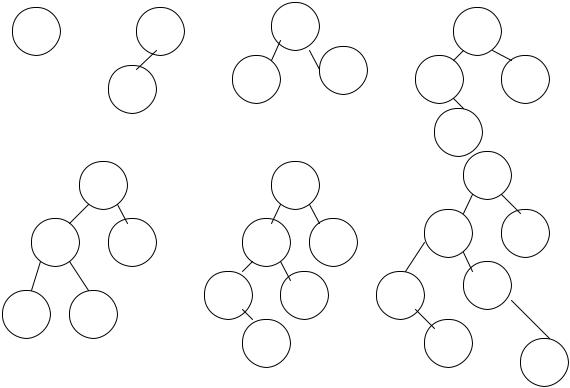
Розглянемо як приклад послідовність ідентифікаторів GA, D1, М22, Е, А12, ВР, F. На мал. проілюстрований весь процес побудови бінарного дерева для цієї послідовності ідентифікаторів.

F

6

7

Рис. 13.2. Покрокове заповнення бінарного дерева для послідовності ідентифікаторів

GA, D1, М22, Е, А12, ВР, F

Пошук потрібного елемента в дереві виконується по алгоритму, схожому з алгоритмом заповнення дерева.

Крок I. Зробити поточним вузлом дерева кореневу вершину.

Крок 2. Порівняти шуканий ідентифікатор з ідентифікатором, що міститься вузлі дерева.

Крок 3. Якщо ідентифікатори збігаються, то шуканий ідентифікатор знайдений, алгоритм завершується, інакше – треба перейти до кроку 4.

Крок 4. Якщо черговий ідентифікатор менше, то перейти до кроку 5, інакше - перейти до кроку 6.

Крок 5. Якщо в поточного вузла існує ліва вершина, то зробити її поточним вузлом і повернутися до кроку 2, інакше шуканий ідентифікатор не знайдений, алгоритм завершується.

Крок 6. Якщо в поточного вузла існує права вершина, то зробити її поточним вузлом і повернутися до кроку 2, інакше шуканий ідентифікатор не знайдений, алгоритм завершується.

Наприклад, зробимо пошук у дереві, зображеному на мал., ідентифікатора А12. Беремо кореневу вершину (вона стає поточним вузлом), порівнюємо ідентифікатори GA і А12. Шуканий ідентифікатор менше — поточним вузлом стає ліва вершина D1. Знову порівнюємо ідентифікатори. Шуканий ідентифікатор менше — поточним вузлом стає ліва вершина А12. При наступному порівнянні шуканий ідентифікатор знайдений.

Якщо шукати відсутній ідентифікатор — наприклад, АН, — то пошук знову піде від кореневої вершини. Порівнюємо ідентифікатори GA і АН. Шуканий ідентифікатор менше — поточним вузлом стає ліва вершина D1. Знову порівнюємо ідентифікатори. Шуканий ідентифікатор менше — поточним вузлом стає ліва вершина А12. Шуканий ідентифікатор менше, але ліва вершина у вузла А12 відсутня, тому в даному випадку шуканий ідентифікатор не знайдений.

Для даного методу число необхідних порівнянь і форма дерева, що вийшло, багато в чому залежать від того порядку, у якому надходять ідентифікатори. Наприклад, якщо в розглянутому вище прикладі замість послідовності ідентифікаторів GA, D1, М22, Е, А12, ВР, F узяти послідовність А12, GA, D1, М22, Е ВР, F то отримане дерево буде мати, інший вид. А якщо як приклад узяти послідовність ідентифікаторів А, В, С.

ідентифікатора! Іншим недоліком є необхідність роботи з динамічним виділенням пам'ятідля побудови дерева..

Якщо припустити, що послідовність ідентифікаторів у вихідній програмі є статистично неупорядкованою (що в цілому відповідає дійсності), то можна вважати, що побудоване бінарне дерево буде невиродженим. Тоді середній час на заповнення дерева (Т3) і на пошук елемента в ньому (Тn) можна оцінити в такий спосіб :

Тз =N*O(log2 N).

Тn =O(log2 N).

У цілому метод бінарного дерева є досить удалим механізмом для організації таблиць ідентифікаторів. Він знайшов своє застосування в ряді компіляторів. Іноді компілятори будують кілька різних дерев ідентифікаторів різних типів і різної довжини .