
2.3. Алгоритми
2.3.1. Алгоритм Apriori
Виявлення частих наборів об'єктів – операція, що вимагає великої кількості обчислень, а отже, і часу. Алгоритм Apriori описаний в 1994 р. Срікантом Рамакрішнан (Ramakrishnan Srikant) і Ракешом Агравалом (Rakesh Agrawal). Він використовує одну з властивостей підтримки, яка стверджує: підтримка будь-якого набору об'єктів не може перевищувати мінімальної підтримки будь-якої з його підмножин:
![]() ,
за
,
за
![]() .
.
Наприклад, підтримка 3-об'єктного набору {пиво, вода, чіпси} буде завжди менше або дорівнювати підтримці 2-об'єктних наборів {пиво, вода}, {вода, чіпси}, {пиво, чіпси}. Це пояснюється тим, що будь-яка транзакція, яка містить {пиво, вода, чіпси}, містить також і набори {пиво, вода}, {вода, чіпси}, {пиво, чіпси}, причому обернене невірно.
Алгоритм Apriori
визначає набори, що часто зустрічаються
за кілька етапів. На
![]() -му
етапі визначаються всі
-му
етапі визначаються всі
![]() -елементні
набори, що часто зустрічаються. Кожен
етап складається з двох кроків: формування
кандидатів (candidate generation) і підрахунку
підтримки кандидатів (candidate counting).
-елементні
набори, що часто зустрічаються. Кожен
етап складається з двох кроків: формування
кандидатів (candidate generation) і підрахунку
підтримки кандидатів (candidate counting).
Розглянемо
![]() -й
етап. На кроці формування кандидатів
алгоритм створює множину кандидатів з
-й
етап. На кроці формування кандидатів
алгоритм створює множину кандидатів з
![]() -елементних
наборів, чия підтримка поки не
вираховуються. На кроці підрахунку
кандидатів алгоритм сканує множину
транзакцій, обчислюючи підтримку
наборів-кандидатів. Після сканування
відкидаються кандидати, підтримка яких
менша певного мінімуму, визначеного
користувачем, і зберігаються тільки
-елементних
наборів, чия підтримка поки не
вираховуються. На кроці підрахунку
кандидатів алгоритм сканує множину
транзакцій, обчислюючи підтримку
наборів-кандидатів. Після сканування
відкидаються кандидати, підтримка яких
менша певного мінімуму, визначеного
користувачем, і зберігаються тільки
![]() -елементні
набори, що часто зустрічаються. Під час
1-го етапу вибрана множина наборів-кандидатів
містить всі 1-елементні часті набори.
-елементні
набори, що часто зустрічаються. Під час
1-го етапу вибрана множина наборів-кандидатів
містить всі 1-елементні часті набори.
Алгоритм обчислює їх підтримку під час кроку підрахунку кандидатів.
Описаний алгоритм можна записати у вигляді наступного псевдокоду:
L1 = {1-елементні набори, що часто зустрічаються }
для (k=2; Lk-1 <>ø; + +)
Сk=Apriorigen (Fk-l) // генерація кандидатів
для
всіх транзакцій
![]() виконати
виконати
Ct=subset (Ck, t) // видалення надлишкових правил
для
всіх кандидатів
![]() виконати
виконати
с.count + +
кінець для всіх
кінець для всіх
![]() //
відбір кандидатів
//
відбір кандидатів
кінець для
Результат
![]() .
.
Опишемо позначення, які використовуються в алгоритмі:
-
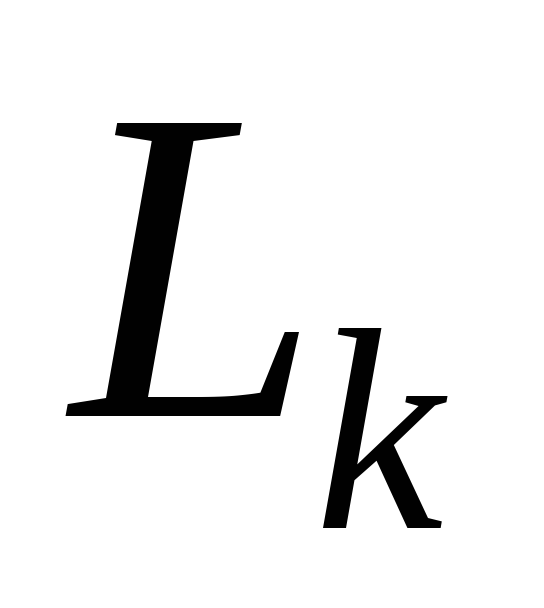 – множина
– множина
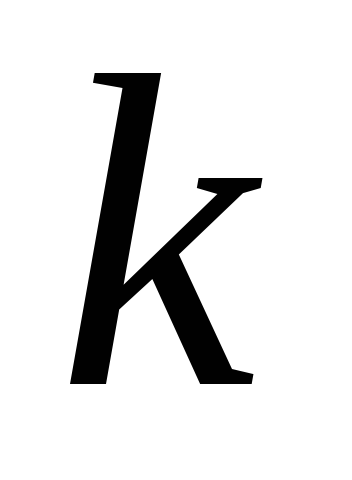 -елементних
частих наборів, чия підтримка не менше
заданої користувачем. Кожен елемент
множини має набір впорядкованих (
-елементних
частих наборів, чия підтримка не менше
заданої користувачем. Кожен елемент
множини має набір впорядкованих (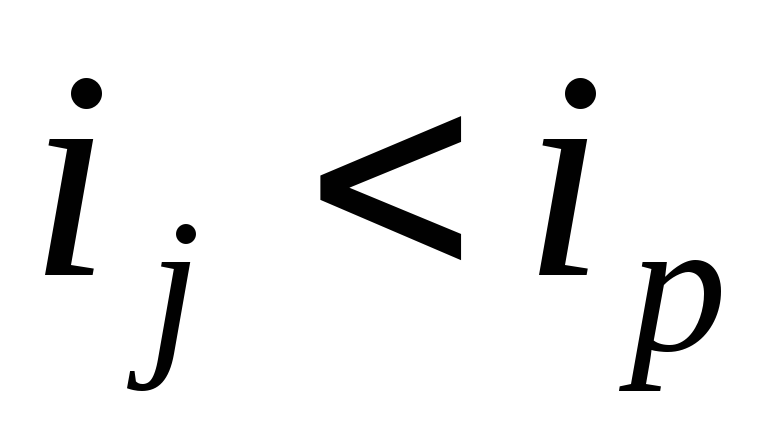 ,
якщо
,
якщо
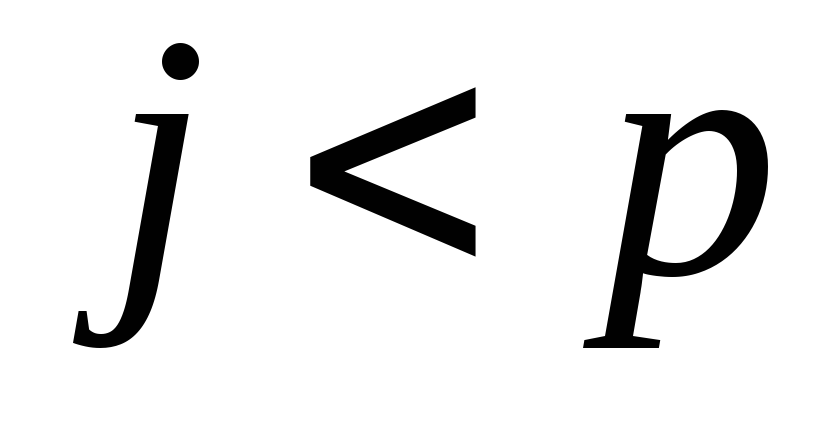 )
елементів
)
елементів
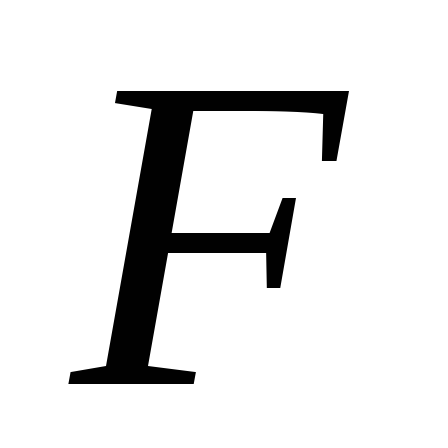 і значення підтримки набору
і значення підтримки набору
 :
:
![]() ,
,
де
![]() ;
;
-
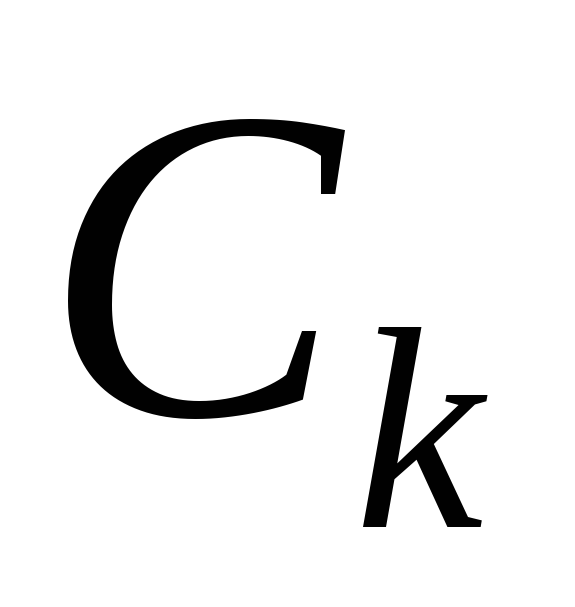 – множина кандидатів
– множина кандидатів
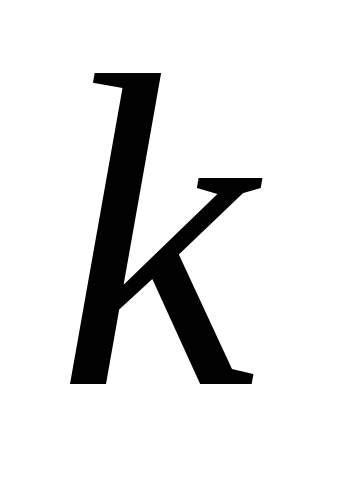 -елементних
наборів, потенційно частих. Кожен
елемент множини має набір упорядкованих
(
-елементних
наборів, потенційно частих. Кожен
елемент множини має набір упорядкованих
(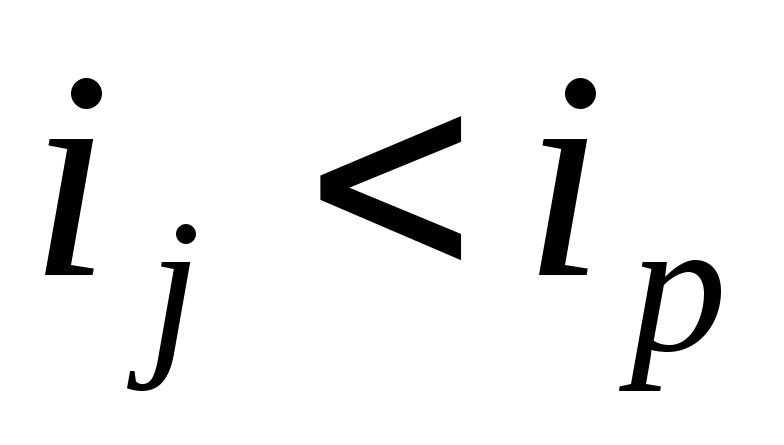 ,
якщо
,
якщо
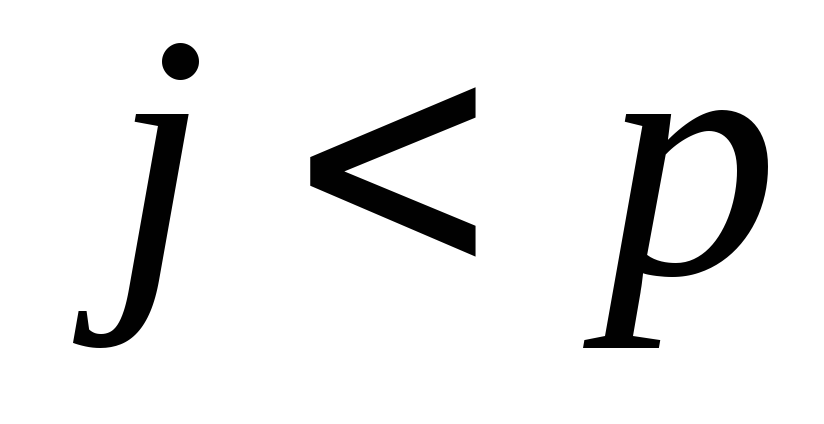 )
елементів
)
елементів
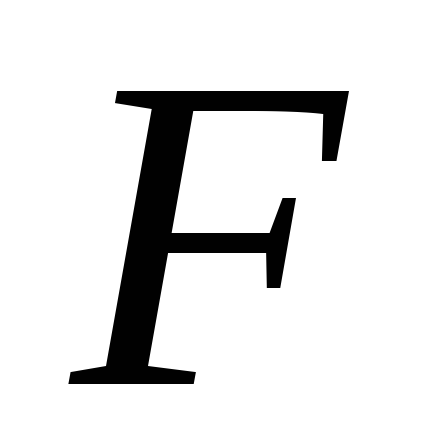 і значення підтримки набору
і значення підтримки набору
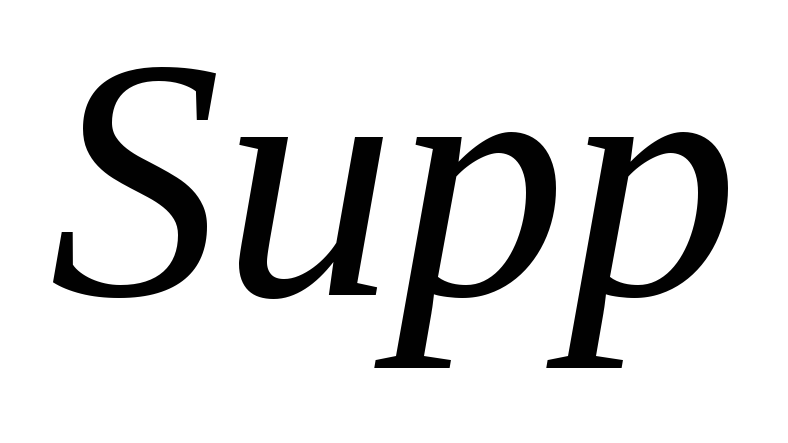 .
.
Опишемо даний алгоритм по кроках.
Крок 1. Присвоїти
![]() і виконати відбір всіх 1-елементних
наборів, у яких підтримка більше
мінімально заданої користувачем
і виконати відбір всіх 1-елементних
наборів, у яких підтримка більше
мінімально заданої користувачем
![]() .
.
Крок 2.
![]() .
.
Крок 3. Якщо не
вдається створювати
![]() -елементні
набори, то завершити алгоритм, інакше
виконати наступний крок.
-елементні
набори, то завершити алгоритм, інакше
виконати наступний крок.
Крок 4. Створити
множину
![]() -елементних
наборів кандидатів у часті набори. Для
цього необхідно об'єднати в
-елементних
наборів кандидатів у часті набори. Для
цього необхідно об'єднати в
![]() -елементні
кандидати (
-елементні
кандидати (![]() )-елементні
часті набори. Кожен кандидат
)-елементні
часті набори. Кожен кандидат
![]() буде формуватися шляхом додавання до
(
буде формуватися шляхом додавання до
(![]() )-елементного
частого набору –
)-елементного
частого набору –
![]() елемента з іншого (
елемента з іншого (![]() )-елементного
частого набору –
)-елементного
частого набору –
![]() .
Причому додається останній елемент
набору
.
Причому додається останній елемент
набору
![]() ,
який за порядком вище, ніж останній
елемент набору
,
який за порядком вище, ніж останній
елемент набору
![]() (
(![]() ).
При цьому перші всі
).
При цьому перші всі
![]() елемента обох наборів однакові (
елемента обох наборів однакові (![]() ).
).
Це може бути записано у вигляді наступного SQL-подібного запиту.
insert into Ck
select p.item1, p.item2, ..., p.itemk-1, q.item k-1
from L k-1 p, L k-1 q
where p.item1=q.item1, p.item2=q.item2,. .., p.itemk-2=q.item k-2,
p.item k-1<q.item k-1
Крок 5. Для кожної
транзакції
![]() з множини
з множини
![]() вибрати кандидатів
вибрати кандидатів
![]() з множини
з множини
![]() присутніх в транзакції
присутніх в транзакції
![]() .
Для кожного набору з побудованої множини
.
Для кожного набору з побудованої множини
![]() видалити набір, якщо хоча б одна з його
(
видалити набір, якщо хоча б одна з його
(![]() )
підмножин не часто зустрічається, тобто
відсутня у множині
)
підмножин не часто зустрічається, тобто
відсутня у множині
![]() .
Це можна записати у вигляді наступного
псевдокоду:
.
Це можна записати у вигляді наступного
псевдокоду:
для
всіх наборів
![]() виконати
виконати
для
всіх (![]() )–піднаборів
)–піднаборів
![]() з
з
![]() виконати
виконати
якщо
(![]() )
то
)
то
видалити
![]() з
з
![]()
Крок 6. Для кожного
кандидата з множини
![]() збільшити значення підтримки на одиницю.
збільшити значення підтримки на одиницю.
Крок 7. Вибрати
тільки кандидатів
![]() з множини
з множини
![]() ,
у яких значення підтримки більше заданої
користувачем
,
у яких значення підтримки більше заданої
користувачем
![]() .
Повернутися до кроку 2.
.
Повернутися до кроку 2.
Результатом роботи
алгоритму є об'єднання всіх множин
![]() для всіх
для всіх
![]() .
.
Розглянемо роботу
алгоритму на прикладі, наведеному в
табл. 6.1, при
![]() .
На першому кроці маємо наступну множину
кандидатів
.
На першому кроці маємо наступну множину
кандидатів
![]() (вказуються ідентифікатори товарів)
(табл. 6.5).
(вказуються ідентифікатори товарів)
(табл. 6.5).
Таблиця 6.5
|
№ |
Набір |
|
|
1 |
{0} |
0 |
|
2 |
{1} |
0,5 |
|
3 |
{2} |
0,75 |
|
4 |
{4} |
0,25 |
|
5 |
{3} |
0,75 |
|
6 |
{5} |
0,75 |
Заданій мінімальній підтримці задовольняють лише кандидати 2, 3, 5 і 6, отже:
![]() ={{1},
{2}, {3}, {5}}.
={{1},
{2}, {3}, {5}}.
На другому кроці
збільшуємо значення
![]() до двох. Так як можна побудувати
2-елементні набори, то отримуємо множину
до двох. Так як можна побудувати
2-елементні набори, то отримуємо множину
![]() (табл. 6.6).
(табл. 6.6).
Таблиця 6.6
|
№ |
Набір |
|
|
1 |
{1,2} |
0,25 |
|
2 |
{1,3} |
0,5 |
|
3 |
{1,5} |
0,25 |
|
4 |
{2,3} |
0,5 |
|
5 |
{2,5} |
0,75 |
|
6 |
{3,5} |
0,5 |
З побудованих кандидатів заданій мінімальній підтримці задовольняють лише кандидати 2, 4, 5 і 6, отже:
![]() ={{1,3},
{2,3}, {2,5}, {3,5}}.
={{1,3},
{2,3}, {2,5}, {3,5}}.
На третьому кроці
перейдемо до створення 3-елементних
кандидатів і підрахунку їх підтримки.
В результаті отримаємо наступну множину
![]() (табл. 6.7).
(табл. 6.7).
Таблиця 6.7
|
№ |
Набір |
|
|
1 |
{2,3,5} |
0,5 |
Даний набір задовольняє мінімальну підтримку, отже:
![]() ={{2,
3,5}}.
={{2,
3,5}}.
Так як 4-елементні набори створити не вдасться, то результатом роботи алгоритму є множина:
![]() ={{1},
{2}, {3}, {5}, {1,3}, {2, 3}, {2, 5}, {3, 5}, {2, 3, 5}}.
={{1},
{2}, {3}, {5}, {1,3}, {2, 3}, {2, 5}, {3, 5}, {2, 3, 5}}.
Для підрахунку підтримки кандидатів потрібно порівняти кожну транзакцію з кожним кандидатом. Очевидно, що кількість кандидатів може бути дуже великою і потрібен ефективний спосіб підрахунку. Набагато швидше і ефективніше використовувати підхід, оснований на зберіганні кандидатів в хеш-дереві. Внутрішні вузли дерева містять хеш-таблиці з покажчиками на нащадків, а листя – на кандидатів. Це дерево використовується при швидкому підрахунку підтримки для кандидатів.
Хеш-дерево будується щоразу, коли формуються кандидати. Спочатку дерево складається тільки з кореня, який є листом, і не містить ніяких кандидатів-наборів. Кожного разу, коли формується новий кандидат, він заноситься в корінь дерева, і так до тих пір, поки кількість кандидатів в корені-листі не перевищить якогось порогу. Як тільки це відбувається, корінь перетворюється в хеш-таблицю, тобто стає внутрішнім вузлом, і для нього створюються нащадки-листя. Усі кандидати розподіляються по вузлах-нащадкам згідно хеш-значенням елементів, що входять у набір. Кожен новий кандидат хеширується на внутрішніх вузлах, поки не досягне першого вузла-листа, де він і буде зберігатися, поки кількість наборів знову ж таки не перевищить порогу.
Після того як
хеш-дерево з кандидатами-наборами
побудовано, легко підрахувати підтримку
для кожного кандидата. Для цього потрібно
"пропустити" кожну транзакцію
через дерево і збільшити лічильники
для тих кандидатів, чиї елементи також
містяться і в транзакції,
![]() .
На кореневому рівні хеш-функція
застосовується до кожного об'єкта з
транзакції. Далі, на другому рівні,
хеш-функція застосовується до других
об'єктів і т. д. На
.
На кореневому рівні хеш-функція
застосовується до кожного об'єкта з
транзакції. Далі, на другому рівні,
хеш-функція застосовується до других
об'єктів і т. д. На
![]() -у
рівні хеширується
-у
рівні хеширується
![]() -елемент,
і так до тих пір, поки не досягнемо листа.
Якщо кандидат, що зберігається в листі,
є підмножиною, що розглядається в
транзакції, збільшуємо лічильник
підтримки цього кандидата на одиницю.
-елемент,
і так до тих пір, поки не досягнемо листа.
Якщо кандидат, що зберігається в листі,
є підмножиною, що розглядається в
транзакції, збільшуємо лічильник
підтримки цього кандидата на одиницю.
Після того як кожна транзакція з вихідного набору даних "пропущена" через дерево, можна перевірити, чи задовольняють значення підтримки кандидатів мінімальному порогу. Кандидати, для яких ця умова виконується, переносяться в розряд тих, що часто зустрічаються. Крім того, слід запам'ятати і підтримку набору, яка стане в нагоді при побудові правил.
Ці ж дії застосовуються
для знаходження (![]() )-елементних
наборів і т. д.
)-елементних
наборів і т. д.
2.3.2. Різновиди алгоритму Apriori
Алгоритм AprioriTid є
різновидом алгоритму Apriori. Відмінною
рисою даного алгоритму є підрахунок
значення підтримки кандидатів не при
скануванні множини
![]() ,
а з допомогою множини
,
а з допомогою множини
![]() ,
що є множингою кандидатів (
,
що є множингою кандидатів (![]() -елементних
наборів) потенційно частих, у відповідність
яким ставиться ідентифікатор TID
транзакцій, в яких вони містяться.
-елементних
наборів) потенційно частих, у відповідність
яким ставиться ідентифікатор TID
транзакцій, в яких вони містяться.
Кожен член множини
![]() є парою виду <TID, {
є парою виду <TID, {![]() }>,
де кожен
}>,
де кожен
![]() є потенційно частим
є потенційно частим
![]() -елементним
набором, представленим в транзакції з
ідентифікатором TID. Множина
-елементним
набором, представленим в транзакції з
ідентифікатором TID. Множина
![]() відповідає множині транзакцій, хоча
кожен об'єкт в транзакції відповідає
одно-об'єктному набору в множині
відповідає множині транзакцій, хоча
кожен об'єкт в транзакції відповідає
одно-об'єктному набору в множині
![]() ,
що містить цей об'єкт. Для
,
що містить цей об'єкт. Для
![]() множина
множина
![]() генерується відповідно до алгоритму,
описаному нижче. Член множини
генерується відповідно до алгоритму,
описаному нижче. Член множини
![]() ,
що відповідає транзакції
,
що відповідає транзакції
![]() ,
є парою наступного виду:
,
є парою наступного виду:
<T.TID, {![]() }>.
}>.
Підмножина наборів
у
![]() з однаковими TID (тобто містяться в одній
і тій же транзакції) називається записом.
Якщо транзакція не містить ні одного
з однаковими TID (тобто містяться в одній
і тій же транзакції) називається записом.
Якщо транзакція не містить ні одного
![]() -елементного
кандидата, то
-елементного
кандидата, то
![]() не буде мати запису для цієї транзакції.
Тобто кількість записів в
не буде мати запису для цієї транзакції.
Тобто кількість записів в
![]() може бути менше, ніж в
може бути менше, ніж в
![]() ,
особливо для великих значень
,
особливо для великих значень
![]() .
Крім того, для великих значень
.
Крім того, для великих значень
![]() кожен запис може бути менше, ніж відповідна
їй транзакція, тому що в транзакції буде
міститися мало кандидатів. Однак для
малих значень
кожен запис може бути менше, ніж відповідна
їй транзакція, тому що в транзакції буде
міститися мало кандидатів. Однак для
малих значень
![]() кожен запис може бути більше, ніж
відповідна транзакція, тому що
кожен запис може бути більше, ніж
відповідна транзакція, тому що
![]() включає всіх кандидатів
включає всіх кандидатів
![]() -елементних
наборів, що містяться в транзакції.
-елементних
наборів, що містяться в транзакції.
Іншим різновидом алгоритму Apriori є алгоритм MSAP (Mining Sequential Alarm Patterns), спеціально розроблений для виконання сиквенціального аналізу збоїв телекомунікаційної мережі.
Він використовує
таку властивість підтримки послідовностей:
для будь-якій послідовності
![]() її підтримка буде менше, ніж підтримка
послідовностей з множини
її підтримка буде менше, ніж підтримка
послідовностей з множини
![]() .
.
Алгоритм MSAP для пошуку подій, що йдуть одна за одної, використовує поняття "термінового вікна" (Urgent Window). Це дозволяє виявляти не просто однакові послідовності подій, а наступні один за одним. У Алгоритм MSAP для пошуку подій, наступних один за одним, використовує поняття "термінового вікна" (Urgent Window). Це дозволяє виявляти не просто однакові послідовності подій, а ті, що йдуть одна за одною. В іншому даний алгоритм працює за тим же принципом, що і Apriori.
