20

Т2. Пошук асоціативних правил

2.1. Постановка завдання

2.2. Подання результатів

2.3. Алгоритми

2.1. Постановка завдання

2.1.1. Формальна постановка задачі

Однією з найбільш поширених завдань аналізу даних є визначення наборів об'єктів, що часто зустрічаються, у множині наборів.

Опишемо це завдання в узагальненому вигляді. Для цього позначимо об'єкти, що складають досліджувані набори (itemsets), наступною множиною:

,

де – об'єкти, що входять в аналізовані набори; – загальна кількість об'єктів.

У сфері торгівлі, наприклад, такими об'єктами є товари, представлені у прайс-листі (табл. 6.1).

Таблиця 6.1

Ідентифікатор	Найменування товару	Ціна
0	Шоколад	30.00
1	Чіпси	12.00
2	Кокоси	10.00
3	Вода	4.00
4	Пиво	14.00
5	Горіхи	15.00

Вони відповідають наступній множині об'єктів:

={Шоколад, чіпси, кокоси, вода, пиво, горіхи}.

Набори об'єктів з множини , що зберігаються в БД і піддаються аналізу, називаються транзакціями. Опишемо транзакцію як підмножину множини:

.

Такі транзакції в магазині відповідають наборам товарів, що купуються споживачем і зберігаються в БД у вигляді товарного чека або накладної. У них перераховуються придбані покупцем товари, їх ціна, кількість та ін. Наприклад, такі транзакції відповідають покупкам, що зроблені споживачами в супермаркеті:

={чіпси, вода, пиво};

={кокоси, вода, горіхи}.

Набір транзакцій, інформація про які доступна для аналізу, позначимо наступною множиною:

,

де – кількість доступних для аналізу транзакцій.

Наприклад, в магазині такою множиною буде:

={{чіпси, вода, пиво},

{Кокоси, вода, горіхи},

{Горіхи, кокоси, чіпси, кокоси, вода},

{Кокоси, горіхи, кокоси}}.

Для використання методів Data Mining множина може бути подана у вигляді табл. 6.2.

Таблиця 6.2

Номер транзакції	Номер товару	Назва товару	Ціна
0	1	Чіпси	12.00
0	3	Вода	4.00
0	4	Пиво	14.00
1	2	Кокоси	10.00
1	1	Вода	4.00
1	5	Горіхи	15.00
2	5	Горіхи	15.00
2	2	Кокоси	10.00
2	1	Чіпси	12.00
2	2	Кокоси	10.00
2	3	Вода	4.00
3	2	Кокоси	10.00
3	5	Горіхи	15.00
3	2	Кокоси	10.00

Множину транзакцій, в які входить об'єкт позначимо наступним чином:

.

У даному прикладі множиною транзакцій, що містять об'єкт вода, є наступна множина:

={{чіпси, вода, пиво},

{Кокоси, вода, горіхи},

{Горіхи, кокоси, чіпси, кокоси, вода}}.

Деякий довільний набір об'єктів (itemset) позначимо наступним чином:

.

Наприклад,

={кокоси, вода}.

Набір, що складається з об'єктів, називається -елементним набором (в даному прикладі це 2-елементний набір).

Множина транзакцій, в які входить набір , позначимо наступним чином:

.

У даному прикладі:

_{{кокоси, вода}}={{кокос, вода, Горіхи},

{Горіхи, кокоси, чіпси, кокоси, вода}}.

Відношення кількості транзакцій, до якого входить набір , до загальної кількості транзакцій називається підтримкою (support) набору і позначається :

.

Для набору {кокоси, вода} підтримка дорівнює 0,5, тому що даний набір входить у дві транзакції (з номерами 1 і 2), а всього транзакцій 4.

При пошуку аналітик може вказати мінімальне значення підтримки цікавлячих його наборів . Набір називається частим (large itemset), якщо значення його підтримки більше мінімального значення підтримки, заданого користувачем:

.

Таким чином, при пошуку асоціативних правил потрібно знайти множину всіх частих наборів:

.

У даному прикладі частими наборами при є наступні:

{Чіпси} ;

{Чіпси, вода} ;

{Кокоси} ;

{Кокоси, вода} ;

{Кокоси, вода, горіхи} ;

{Кокоси, горіхи} ;

{Вода} ;

{Вода, горіхи} ;

{Горіхи} .

2.1.2. Сіквенціальний аналіз

При аналізі часто викликає інтерес послідовність подій, що відбуваються. При виявленні закономірностей у таких послідовностях можна з деякою часткою ймовірності передбачати появу подій у майбутньому, що дозволяє приймати більш правильні рішення.

Послідовністю називається упорядкована множна об'єктів. Для цього на множині повинно бути задано відношення порядку.

Тоді послідовність об'єктів можна описати в наступному вигляді:

, де .

Наприклад, у випадку з покупками в магазинах таким відношенням порядку може виступати час покупок. Тоді послідовність

S={(вода, 02.03.2003), (чіпси, 05.03.2003), (пиво, 10.03.2003)}

можна інтерпретувати як покупки, які робляться однією людиною в різний час (спочатку була куплена вода, потім чіпси, а потім пиво).

Розрізняють два види послідовностей: з циклами і без циклів. У першому випадку допускається входження в послідовність одного і того ж об'єкта на різних позиціях:

, де a .

Кажуть, що транзакція містить послідовність , якщо і об'єкти, що входять в входять і в множину зі збереженням відносини порядку. При цьому допускається, що в множині між об'єктами з послідовності можуть перебувати інші об'єкти.

Підтримкою послідовності називається відношення кількості транзакцій, до якої входить послідовність , до загальної кількості транзакцій. Послідовність є частою, якщо її підтримка перевищує мінімальну підтримку, задану користувачем:

.

Завданням сіквенціального аналізу є пошук всіх частих послідовностей:

.

Основною відмінністю завдання сіквенціального аналізу від пошуку асоціативних правил є встановлення відношення порядку між об'єктами множини . Дане відношення може бути визначене різними способами. При аналізі послідовності подій, що відбуваються в часі, об'єктами множини є події, а відношення порядку відповідає хронології їх появи.

Наприклад, при аналізі послідовності покупок в супермаркеті наборами є покупки, які робляться в різний час одними і тими ж покупцями, а відношенням порядку в них є хронологія покупок:

={{(вода), (пиво)},

{(Кокоси, вода), (пиво), (вода, шоколад, кокоси)},

{(Пиво, чіпси, вода), (пиво)}}.

Природно, що в цьому випадку виникає проблема ідентифікації покупців. На практиці вона вирішується введенням дисконтних карт, що мають унікальний ідентифікатор. Дану множину можна подати у вигляді табл. 6.3.

Таблиця 6.3

ID покупця	Послідовність покупок
0	(Пиво), (вода)
1	(Кокоси, вода), (пиво), (вода, шоколад, кокоси)
2	(Пиво, чіпси, вода), (пиво)

Інтерпретувати таку послідовність можна наступним чином: покупець з ідентифікатором 1 спочатку купив кокоси і воду, потім купив пиво, в останній раз він купив воду, шоколад і кокоси.

Підтримка, наприклад, послідовності {(пиво), (вода)} складе 2/3, тому що вона зустрічається у покупців з ідентифікаторами 0 і 1. В останнього покупця також зустрічається набір {(пиво), (вода)}, але не зберігається послідовність (він купив спочатку воду, а потім пиво).

Сіквенціальний аналіз актуальний і для телекомунікаційних компаній. Основна проблема, на вирішення якої він використовується, – це аналіз даних про аварії на різних вузлах телекомунікаційної мережі. Інформація про послідовність здійснення аварій може допомогти в виявленні неполадок та попередження нових аварій. Дані для такого аналізу можуть бути подані, наприклад, у вигляді табл. 6.4.

Таблиця 6.4

Дата	Час	Джерело помилки	Код джерела	Код помилки	...
01.01.03	15:04:23	Станція 1	1001		...
01.01.03	16:45:46	Станція 1	1001		...
01.01.03	18:32:26	Станція 4	1004		...
01.01.03	20:07:11	Станція 5	1005		...
01.01.03	20:54:43	Станція 1	1001		...
...	...	...	...	...	...

У цьому завданню об'єктами множини є коди помилок, що виникають в процесі роботи телекомунікаційної мережі. Послідовність містить збої, що відбуваються на станції з ідентифікатором . Їх можна подати у вигляді пар (), де – код помилки, a – час, коли вона сталася. Таким чином, послідовність збоїв на станції з ідентифікатором буде мати наступний вигляд:

.

Для даних, наведених у табл. 6.4, транзакції будуть наступні:

={(a, 15:04:23 01.01.03), (f, 16:45:46 01.01.03), (q, 20:54:43 01.01.03),...};

={(z, 18:32:26 01.01.03 ),...};

={(h, 20:07:1101.01.03 ),...}.

Відношення порядку в даному випадку задається щодо часу появи помилки (значення ).

Рис. 6.1. Послідовність збоїв на телекомунікаційній станції

При аналізі такої послідовності важливим є визначення інтервалу часу між збоями. Воно дозволяє передбачити момент і характер нових збоїв, а отже, провести профілактичні заходи. З цієї причини при аналізі даних інтерес викликає не просто послідовність подій, а збої, які відбуваються один за одним. Наприклад, на рис. 6.1 зображена часова шкала послідовності збоїв, що відбуваються на одній станції. При визначенні підтримки, наприклад, для послідовності {А, С} враховуються тільки наступні набори: {{А, 0:12), (С, 0:25)}, {(А, 0:38), (С, 1:42)}, {(А, 1:25), (С, 1:42)}. При цьому не враховуються послідовності: {(А, 0:12), (С, 1:42)}, {(А, 0:12), (С, 1:51)}, {{А, 0:38), (С, 1:51)} і {{А, 1:25), (С, 1:51)}, оскільки вони не слідують безпосередньо один за одним.

2.1.3. Різновиди завдання пошуку асоціативних правил

У багатьох прикладних областях об'єкти множини природним чином об'єднуються в групи, які в свою чергу також можуть об'єднуватися в більш загальні групи, і т. д. Таким чином, виходить ієрархічна структура об'єктів, подана на рис. 6.2.

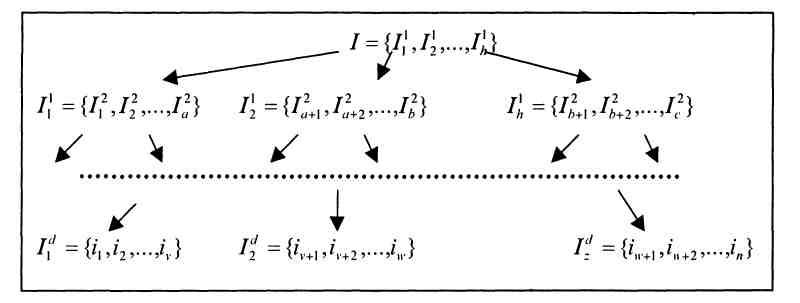
Рис. 6.2. Ієрархічне подання об'єктів множини

Для прикладу, наведеного в табл. 6.1, такої ієрархії може бути наступна категоризація товарів:

• напої;

  • алкогольні;

    • пиво;

  • безалкогольні;

    • вода;

• їжа;

  • шоколад;

  • чіпси;

  • кокоси;

  • горіхи.

Наявність ієрархії змінює уявлення про те, коли об'єкт присутній в транзакції . Очевидно, що підтримка не окремого об'єкта, а групи, до якої він входить, більше:

,

де .

Це пов'язано з тим, що при аналізі груп підраховуються не тільки транзакції, в які входить окремий об'єкт, а й транзакції, що містять всі об'єкти аналізованої групи. Наприклад, якщо підтримка

{Кокоси, вода} = 2/4, то підтримка {їжа, напої} = 2/4, оскільки об'єкти груп їжа і напої входять в транзакції з ідентифікаторами 0, 1 і 2.

Використання ієрархії дозволяє визначити зв'язки, що входять до більш високі рівні ієрархії, оскільки підтримка набору може збільшуватися, якщо підраховується входження групи, а не її об'єкта. Крім пошуку наборів, що часто зустрічаються у транзакціях, що складаються з об'єктів або груп одного рівня ієрархії , можна розглядати також змішані набори об'єктів і груп . Це дозволяє розширити аналіз і отримати додаткові знання.

При ієрархічній структурі об'єктів можна варіювати характер пошуку змінюючи аналізований рівень. Очевидно, що чим більше об'єктів у множині , тим більше об'єктів у транзакціях і частих наборах. Це в свою чергу збільшує час пошуку та ускладнює аналіз результатів. Зменшити або збільшити кількість даних можна за допомогою ієрархічного подання аналізованих об'єктів. Переміщаючись вгору по ієрархії, узагальнюємо дані і зменшуємо їхню кількість, і навпаки.

Недоліком узагальнення об'єктів є менша корисність отриманих знань, тому що в цьому випадку вони відносяться до груп товарів, що не завжди прийнятно. Для досягнення компромісу між аналізом груп і аналізом окремих об'єктів часто поступають таким чином: спочатку аналізують групи, а потім, в залежності від отриманих результатів, досліджують об'єкти груп, що зацікавили аналітика. У будь-якому випадку можна стверджувати, що наявність ієрархії в об'єктах і її використання в задачі пошуку асоціативних правил дозволяє виконувати більш гнучкий аналіз і отримувати додаткові знання.

У розглянутій задачі пошуку асоціативних правил наявність об'єкта в транзакції визначалося тільки його присутністю в ній () або відсутністю (). Часто об'єкти мають додаткові атрибути, як правило, чисельні. Наприклад, товари в транзакції мають атрибути: ціна та кількість. При цьому наявність об'єкта в наборі може визначатися не просто фактом його присутності, а виконанням умови по відношенню до певного атрибуту. Наприклад, при аналізі транзакцій, здійснених покупцем, може цікавити не просто наявність товару, що купується, а товару, що купується за деякою ціною.

Для розширення можливостей аналізу за допомогою пошуку асоціативних правил в досліджувані набори можна додавати додаткові об'єкти. У загальному випадку вони можуть мати природу, відмінну від основних об'єктів. Наприклад, для визначення товарів, що мають більший попит у залежності від місця розташування магазину, в транзакції можна додати об'єкт, що характеризує район.