
shpora / ryadi
.doc
Ряд
– сума
![]() ;
an
– общий член ряда.
;
an
– общий член ряда.
Частичная сумма
![]() .
.
Ряд называется
сходящимся,
если существует
![]() .
.
Ряд называется
расходящимся,
если не
существует
![]() .
.
Сходимость/расходимость рядов:
Если
![]() ряд расходится.
ряд расходится.
Ряды с положительными членами.
![]()
|
|
Если сходится (2) сходится (1)
Если расходится (1) расходится (2) |
Признак Даламбера
|
|
Ряд сходится Ряд расходится Нужны доп. исследования |
Интегральный признак Коши
|
|
|
Обобщенные гармонические ряды
|
|
Сходится
при Расходится
при |
Предельная теорема сравнения.
![]() ряды (1) и (2)
сходятся/расходятся одновременно.
ряды (1) и (2)
сходятся/расходятся одновременно.
Ряды с произвольными членами.
|
|
Если (2) сходятся: (1) – абсолютно сходящийся (2) расход., (1) – сход.: (1) – условно сходящийся |
Теорема об абсолютной сходимости:
Если (2) – сходится, то (1) – тоже сходится (обратное неверно)
|
Знакочередующиеся ряды.
|
Признак Лейбница (только для (*)) (*) сходится, если: |

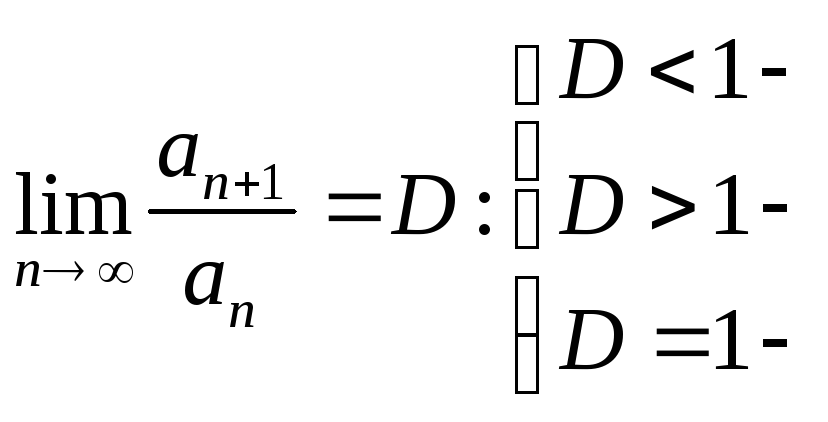
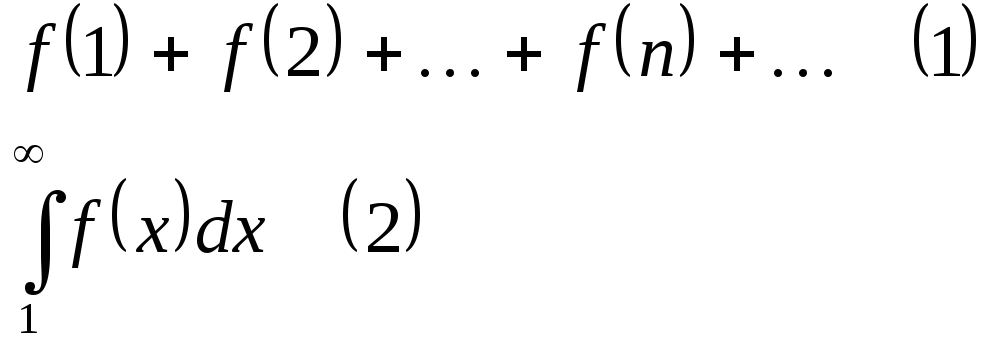 (1)
и (2) сходятся/расходятся одновременно.
(1)
и (2) сходятся/расходятся одновременно.