боднар / Lab 3 DES

R3: 1101 1000 1100 0111 1111 0001 0011 0101

Получаем последовательность из 48-ми битным входом:

E(R3): 111011 110001 011000 001111 111110 100010 100110 101011

Произведем операцию XOR (сложение по модулю 2) по формуле  E(R_n-1) XOR ключ K_n. На первой итерации это K₄ E(R₃):

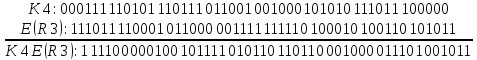
Осуществим S-подстановку за таблицами, преобразуем 6-битовые числа в 4-битовые:

K₄ E(R₃) = B₁B₂B₃B₄B₅B₆B₇B₈:

111100 000100 101111 010110 110110 001000 011101 001011

Номер S-блока	Исходное число	Строка; столбец	Значение	Двоичное значение
S1	111100	2; 14	5	0101
S2	000100	0; 2	8	1000
S3	101111	3; 7	7	0111
S4	010110	0; 11	5	0101
S5	110110	2; 11	5	0101
S6	001000	0; 4	9	1001
S7	011101	1; 14	8	1000
S8	001011	1; 5	3	0011

S(B₁)S(B₂)S(B₃)S(B₄)S(B₅)S(B₆)S(B₇)S(B₈):

0101 1000 0111 0101 0101 1001 1000 0011

Выполним функцию перестановки за таблицей P:

16	7	20	21
29	12	28	17
1	15	23	26
5	18	31	10
2	8	24	14
32	27	3	9
19	13	30	6
22	11	4	25

f = P[S(B₁)S(B₂)S(B₃)S(B₄)S(B₅)S(B₆)S(B₇)S(B₈)]:

1011 0100 0000 1111 1011 1000 0000 0111

Конечный результат после 4 итерации:

L3: 1001 1010 0001 1110 1110 0111 0011 0101

f(R₃,K₄): 1011 0100 0000 1111 1011 1000 0000 0111

R₄ = L₃ f(R₃,K₄):

R4: 0010 1110 0001 0001 0101 1111 0011 0010

L₄ = R₃: 1101 1000 1100 0111 1111 0001 0011 0101

Итерация 5.

Расширяем входное значение до 48 битов для последующего сложения с ключом раунда. Над 32-битным входом выполняется расширяющая перестановка согласно таблице E:

32	1	2	3	4	5
4	5	6	7	8	9
8	9	10	11	12	13
12	13	14	15	16	17
16	17	18	19	20	21
20	21	22	23	24	25
24	25	26	27	28	29
28	29	30	31	32	1

R4: 0010 1110 0001 0001 0101 1111 0011 0010

Получаем последовательность из 48-ми битным входом:

E(R4): 000101 011100 000010 100010 101011 111111 110110 100100

Произведем операцию XOR (сложение по модулю 2) по формуле  E(R_n-1) XOR ключ K_n. На первой итерации это K₅ E(R₄):

Осуществим S-подстановку за таблицами, преобразуем 6-битовые числа в 4-битовые:

K₅ E(R₄) = B₁B₂B₃B₄B₅B₆B₇B₈:

000010 101010 100101 111011 110101 110101 000110 110011

Номер S-блока	Исходное число	Строка; столбец	Значение	Двоичное значение
S1	000010	0; 1	4	0100
S2	101010	2; 5	4	0100
S3	100101	3; 2	13	1101
S4	111011	3; 13	7	0111
S5	110101	3; 10	0	0000
S6	110101	3; 10	1	0001
S7	000110	0; 3	14	1110
S8	110011	3; 9	12	1100

S(B₁)S(B₂)S(B₃)S(B₄)S(B₅)S(B₆)S(B₇)S(B₈):

0100 0100 1101 0111 0000 0001 1110 1100

Выполним функцию перестановки за таблицей P:

16	7	20	21
29	12	28	17
1	15	23	26
5	18	31	10
2	8	24	14
32	27	3	9
19	13	30	6
22	11	4	25

f = P[S(B₁)S(B₂)S(B₃)S(B₄)S(B₅)S(B₆)S(B₇)S(B₈)]:

1000 1101 0101 0001 1011 0101 0011 0001

Конечный результат после 5 итерации:

L4: 1101 1000 1100 0111 1111 0001 0011 0101

f(R₄,K₅): 1000 1101 0101 0001 1011 0101 0011 0001

R₅ = L₄ f(R₄,K₅):

R5: 0111 0101 1001 0110 0100 0100 0000 0100

L₅ = R₄: 0010 1110 0001 0001 0101 1111 0011 0010

Итерация 6.

Расширяем входное значение до 48 битов для последующего сложения с ключом раунда. Над 32-битным входом выполняется расширяющая перестановка согласно таблице E:

32	1	2	3	4	5
4	5	6	7	8	9
8	9	10	11	12	13
12	13	14	15	16	17
16	17	18	19	20	21
20	21	22	23	24	25
24	25	26	27	28	29
28	29	30	31	32	1

R5: 0111 0101 1001 0110 0100 0100 0000 0100

Получаем последовательность из 48-ми битным входом:

E(R5): 001110 101011 110010 101110 101000 001000 000000 001100

Произведем операцию XOR (сложение по модулю 2) по формуле  E(R_n-1) XOR ключ K_n. На первой итерации это K₆ E(R₅):

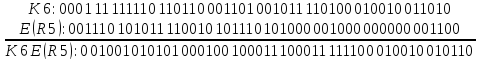
Осуществим S-подстановку за таблицами, преобразуем 6-битовые числа в 4-битовые:

K₆ E(R₅) = B₁B₂B₃B₄B₅B₆B₇B₈:

001001 010101 000100 100011 100011 111100 010010 010110

Номер S-блока	Исходное число	Строка; столбец	Значение	Двоичное значение
S1	001001	1; 4	14	1110
S2	010101	1; 10	1	0001
S3	000100	0; 2	9	1001
S4	100011	3; 1	15	1111
S5	100011	3; 1	8	1000
S6	111100	2; 14	11	1011
S7	010010	0; 9	12	1100
S8	010110	0; 11	14	1110

S(B₁)S(B₂)S(B₃)S(B₄)S(B₅)S(B₆)S(B₇)S(B₈):

1110 0001 1001 1111 1000 1011 1100 1110

Выполним функцию перестановки за таблицей P:

16	7	20	21
29	12	28	17
1	15	23	26
5	18	31	10
2	8	24	14
32	27	3	9
19	13	30	6
22	11	4	25

f = P[S(B₁)S(B₂)S(B₃)S(B₄)S(B₅)S(B₆)S(B₇)S(B₈)]:

1001 1101 1111 0010 1111 0011 0110 0001

Конечный результат после 6 итерации:

L5: 1101 1000 1100 0111 1111 0001 0011 0101

f(R₅,K₆): 1001 1101 1111 0010 1111 0011 0110 0001

R₆ = L₅ f(R₅,K₆):

R6: 0100 0101 0011 0101 0000 0010 0101 0100

L₆ = R₅: 0111 0101 1001 0110 0100 0100 0000 0100

Итерация 7.

Расширяем входное значение до 48 битов для последующего сложения с ключом раунда. Над 32-битным входом выполняется расширяющая перестановка согласно таблице E:

32	1	2	3	4	5
4	5	6	7	8	9
8	9	10	11	12	13
12	13	14	15	16	17
16	17	18	19	20	21
20	21	22	23	24	25
24	25	26	27	28	29
28	29	30	31	32	1

R6: 0100 0101 0011 0101 0000 0010 0101 0100

Получаем последовательность из 48-ми битным входом:

E(R6): 010000 001010 100110 101010 100000 000100 001010 101000

Произведем операцию XOR (сложение по модулю 2) по формуле  E(R_n-1) XOR ключ K_n. На первой итерации это K₇ E(R₆):

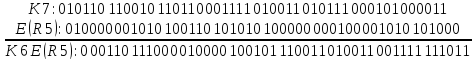
Осуществим S-подстановку за таблицами, преобразуем 6-битовые числа в 4-битовые:

K₇ E(R₆) = B₁B₂B₃B₄B₅B₆B₇B₈:

000110 111000 010000 100101 110011 010011 001111 111011

Номер S-блока	Исходное число	Строка; столбец	Значение	Двоичное значение
S1	000110	0; 3	1	0001
S2	111000	2; 12	9	1001
S3	010000	0; 8	1	0001
S4	100101	3; 2	0	0000
S5	110011	3; 9	15	1111
S6	010011	1; 9	1	0001
S7	001111	1; 7	10	1010
S8	111011	3; 13	5	0101

S(B₁)S(B₂)S(B₃)S(B₄)S(B₅)S(B₆)S(B₇)S(B₈):

0001 1001 0001 0000 1111 0001 1010 0101

Выполним функцию перестановки за таблицей P:

16	7	20	21
29	12	28	17
1	15	23	26
5	18	31	10
2	8	24	14
32	27	3	9
19	13	30	6
22	11	4	25

f = P[S(B₁)S(B₂)S(B₃)S(B₄)S(B₅)S(B₆)S(B₇)S(B₈)]:

0010 0101 0000 1100 0110 1100 1010 0011

Конечный результат после 7 итерации:

L6: 0111 0101 1001 0110 0100 0100 0000 0100

f(R₆,K₇): 0010 0101 0000 1100 0110 1100 1010 0011

R₇ = L₆ f(R₆,K₇):

R7: 0101 0000 1001 1010 0010 1000 1010 0111

L₇ = R₆: 0100 0101 0011 0101 0000 0010 0101 0100

Итерация 8.

Расширяем входное значение до 48 битов для последующего сложения с ключом раунда. Над 32-битным входом выполняется расширяющая перестановка согласно таблице E:

32	1	2	3	4	5
4	5	6	7	8	9
8	9	10	11	12	13
12	13	14	15	16	17
16	17	18	19	20	21
20	21	22	23	24	25
24	25	26	27	28	29
28	29	30	31	32	1

R7: 0101 0000 1001 1010 0010 1000 1010 0111

Получаем последовательность из 48-ми битным входом:

E(R7): 101010 000001 010011 110100 000101 010001 010100 001110

Произведем операцию XOR (сложение по модулю 2) по формуле  E(R_n-1) XOR ключ K_n. На первой итерации это K₈ E(R₇):

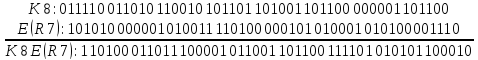
Осуществим S-подстановку за таблицами, преобразуем 6-битовые числа в 4-битовые:

K₈E(R₇) = B₁B₂B₃B₄B₅B₆B₇B₈:

110100 011011 100001 011001 101100 111101 010101 100010

Номер S-блока	Исходное число	Строка; столбец	Значение	Двоичное значение
S1	110100	2; 10	9	1001
S2	011011	1; 13	9	1001
S3	100001	3; 0	1	0001
S4	011001	1; 12	1	0001
S5	101100	2; 6	7	0111
S6	111101	3; 14	8	1000
S7	010101	1; 10	5	0101
S8	100010	2; 1	11	1011