Контрольна робота5

Контрольна робота №1.

І семестр, спеціальність “Фізика”

Варіант 1: Варіант 2:

1. Розв’зати систему рівнянь матричним методом:

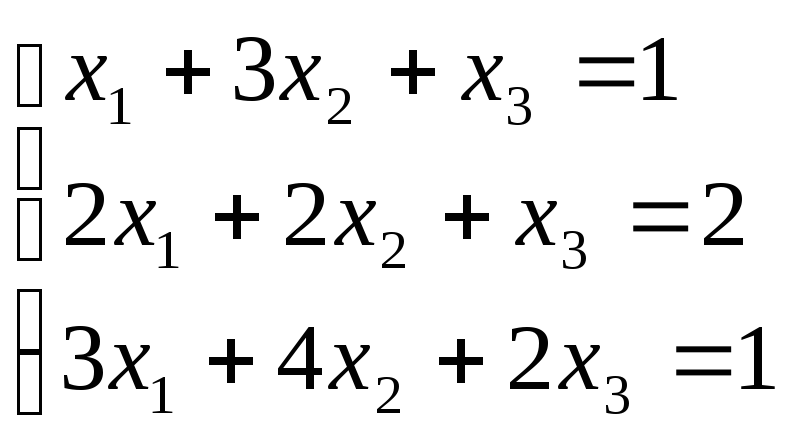
2. Нехай у множині 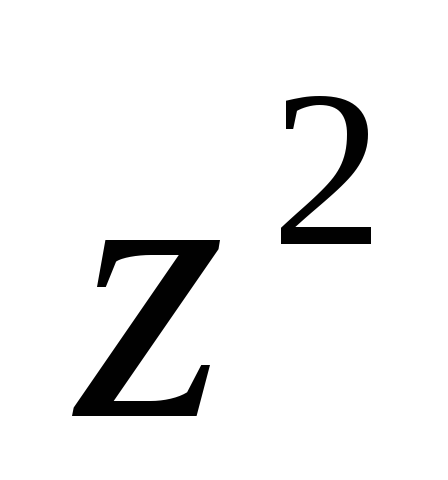задано 2. Чи є множина всіх чисел крат- операцію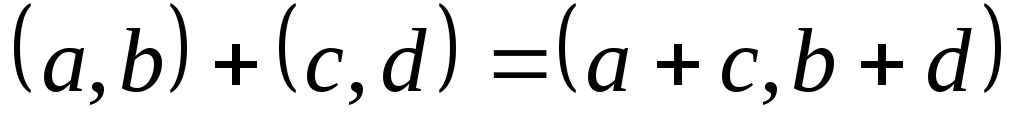 них 7 абелевою групою від-

Чи є алгебра абеловою групою? носно операції додавання

(множення)?

3. Побудувати простір розв’язків системи лінійних рівнянь.

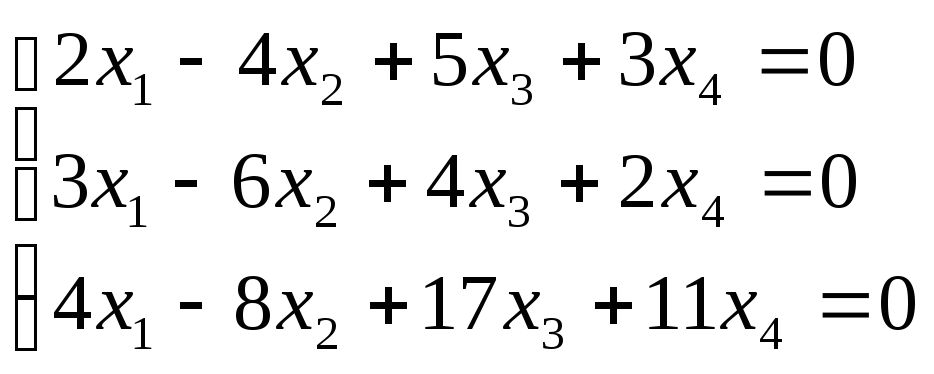
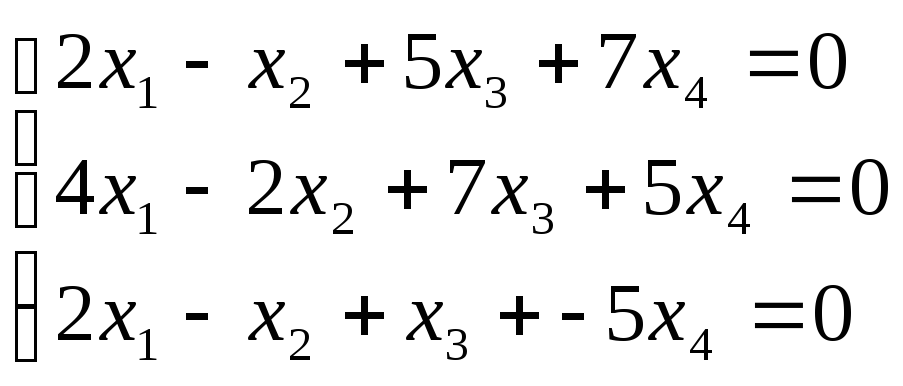
3. Знайти ранг системи векторів, один з базисів системи векторів та виразити вектор, який входить до базису через базисні:

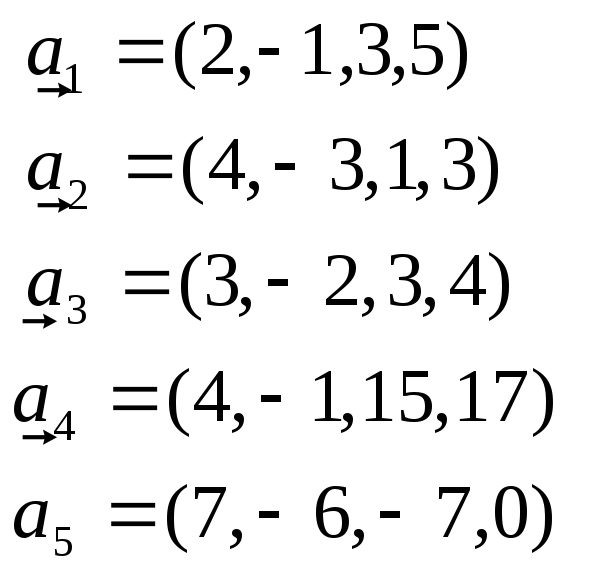
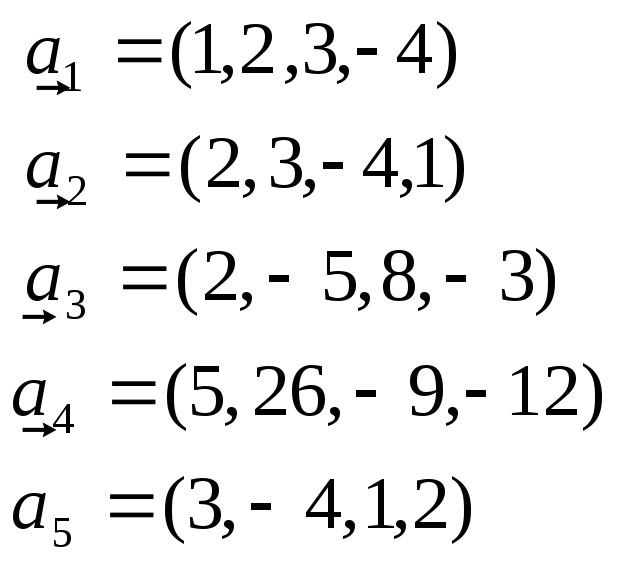
3. Побудувати ортогональний базис підпростору натянутого на системувекторів:

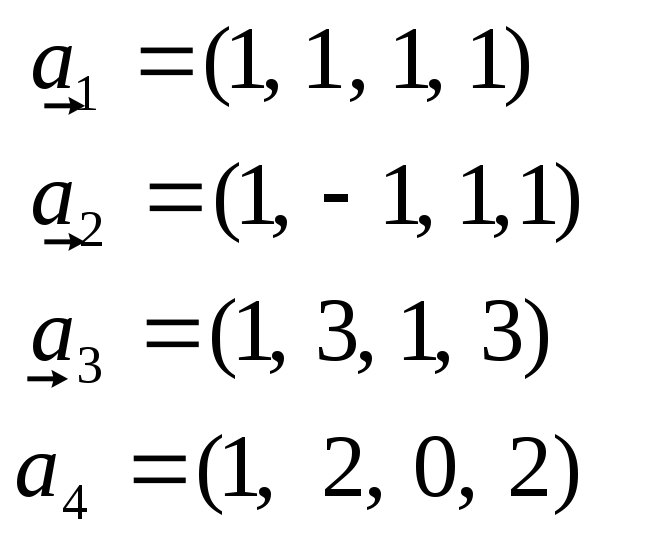
Контрольна робота № 2.

Варіант 1: Варіант 2:

1. побудувати ортонормований базис підпростору, натянутого на слідуючу истему векторів:

2. Виконати дії:

1. а)

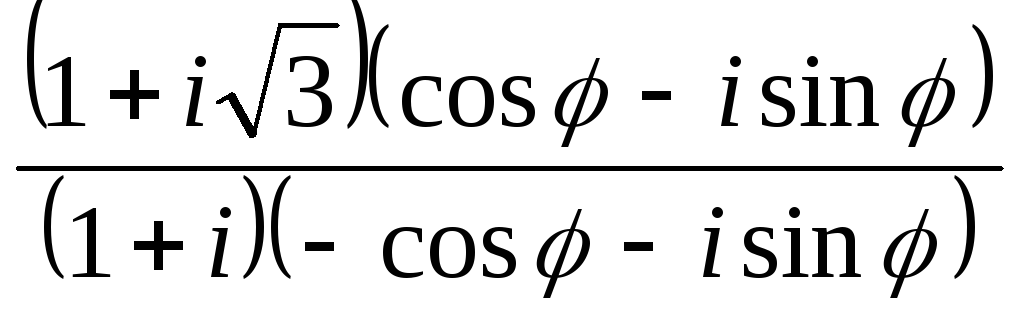
б) б)

І розв’язати рівняння:

2. Серед чисел, які задовільняють умову вибрати ті, які мають найменший додатній аргумент:

2. Оператор задано правилом:

1. Довести чи є він лінійним і знайти його матрицю в базисі .

2. Знайти ядро і область значень оператора.

3. Вияснити чи зводиться матриця лінійного оператора до діогонального виду за допомогою переходу до іншого базису. Знайти цей базис і відповідну йому матрицю.

Контрольна робота №1.

ІІ семестр, спеціальність “Фізика”.

Варіант 1:

1. На прямих знайти відповідно т. А і В такі, щоб пряма АВ мала кутовий коефіцієнт, рівний 3, і щоб довжина відрізка АВ дорівнювала .

2. Дано рівняння висот трикутника АВС: і координати вершини А(2,2). Скласти рівняння сторін трикутника.

3. Записати рівняння площини, яка проходить через т.А(5.4.3) і відсікає рівні відрізки на осях координат.

4. Через пряму провести площину, яка парлельна прямій .

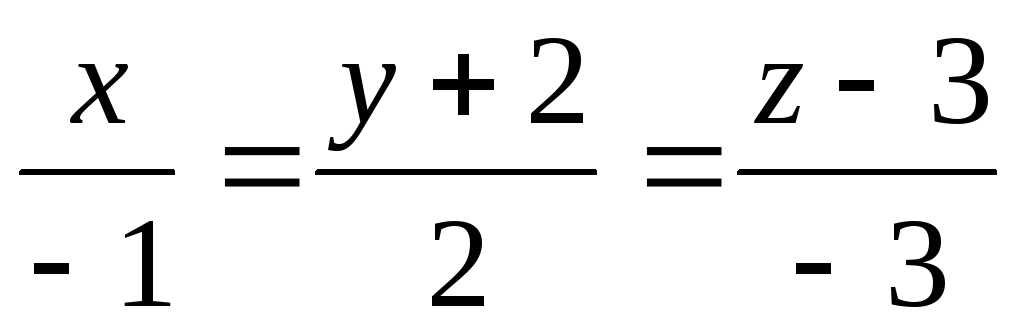5. Обчислити площу паралелограма, побудуваного на векторах:

і .

Варіант 2:

1. Дано дві точки А(3,5) і В(-1,-2). На прямій знайти точку С таку, щоб площа АВС дорівнювала 1.

2. Дано вершини трикутника А(1,1), В(10,13), С(13,6). Записати рівняння бісектриси кута А.

3. Записати рівняння площини, яка проходить через т.А(2,-1,4), В(3,2,-1) перпендикулярно площині .

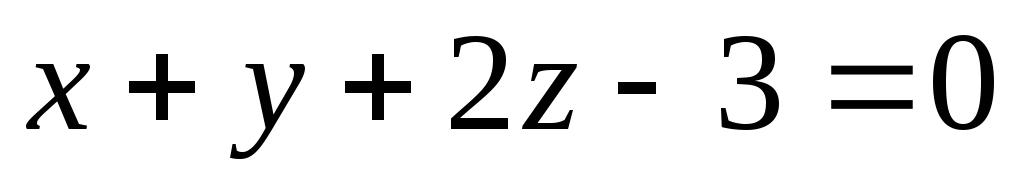4. Дано пряму 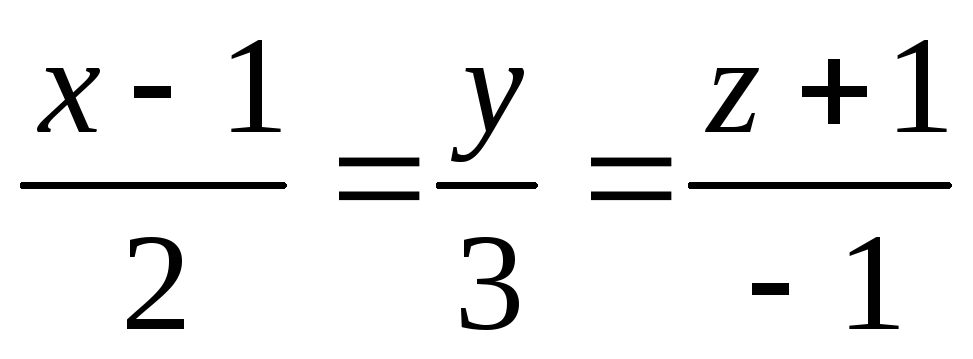і т.М(1,1,1), яка їй не належить. Знайти точку М’ симетричну т. М відносно даної прямої.

5. Обчислити площу трикутника з вершинами А(1,1,1), В(2,3,4), С(4,3,2).