
- •Вопрос №21. Гидравлические сопротивления. Формулы Дарси-Вейсбаха.
- •4.4. Потери напора при турбулентном течении жидкости
- •Коэффициент шероховатости n
- •Определение нормальной глубины
- •7.2. Поршневые насосы
- •Подбор центробежных насосов
- •Подбор насоса к насосной установке по характеристикам
- •Подбор насоса по коэффициенту быстроходности
- •Конструкции осевых насосов и насосных установок
- •Еденицы измерения:
Вопрос №2 Физические свойства жидкостей
Плотность и удельный вес. К основным физическим свойствам жидкостей следует отнести те её свойства, которые определяют особенности поведения жидкости при её движении. Такими являются свойства, характеризующие концентрацию жидкости в пространстве, свойства, определяющие процессы деформации жидкости, определяющие величину внутреннего трения в жидкости при её движении, поверхностные эффекты.
Важнейшим физическим свойством жидкости, определяющим её концентрацию в пространстве, является плотность жидкости. Под плотностью жидкости понимается масса единицы объёма жидкости:

где: М - масса жидкости,
W - объём, занимаемый жидкостью.
В международной системе единиц СИ масса вещества измеряется в кг, объём жидкого тела в м 3 ,тогда размерность плотности жидкости в системе единиц СИ - кг/м 3. В системе единиц СГС плотность жидкости измеряется в г/см 3.
Величины плотности реальных капельных жидкостей в стандартных условиях изменяются в системе единиц СИ в широких пределах от 700 кг/м 3 до 1800 кг/м 3, а плотность ртути достигает 13550 кг/м ,плотность чистой воды составляет 998 кг/м 3. В системе единиц СГС пределы изменения плотности жидкости от 0,7 г/см до 1,8 г/см 3, плотность чистой воды 0,998 г/см . Величины плотности газов меньше плотности капельных жидкостей приблизительно на три порядка, т.е. в системе единиц СИ плотности газов при атмосферном давлении и температуре О °С изменяются в пределах от 0,09 кг/м 3 до 3,74 кг/м ,плотность воздуха составляет 1,293 кг/м 3.
|
Плотность капельных жидкостей при стандартных условиях, р кг/м 3 |
Плотность газов при атмосферном давлении и температуре 0 °С, р кг/м 3 | |||
|
Азотная кислота |
1510 |
Азот |
1,251 | |
|
Анилин |
1020 |
Аммиак |
0,771 | |
|
Ацетон |
791 |
Аргон |
1,783 | |
|
Бензин |
680-720 |
Ацетилен |
1,173 | |
|
Бензол |
879 |
Водород |
0,090 | |
|
Бром |
3120 |
Воздух |
1,293 | |
|
Вода, Н2О |
998 |
Гелий |
0,178 | |
|
Вода тяжёлая, DaO |
1109 |
Кислород |
1,429 | |
|
Глицерин |
1260 |
Криптон |
3,740 | |
|
Морская вода |
1010-1030 |
Неон |
0,900 | |
|
Нефть |
760-995 |
Озон |
2,139 | |
|
Серная кислота |
1830 |
Углекислота, СОа |
1,977 | |
|
Этиловый спирт |
790 |
Хлор |
3,220 | |
Плотность капельных жидкостей и газов зависит от температуры и давления. Зависимость величины плотности жидкости и газа при температуре отличной от 20 °С определяется по формуле Д.И. Менделеева:

где: р и р20 - плотности жидкости (газа) при температурах соответственно
ГиГо=20°С,
βi - коэффициент температурного расширения.
Исключительными особенностями обладает вода, максимальная плотность которой отмечается при 4 °С
|
Плотность воды при различных температурах и атмосферном давлении | |||||
|
Т,°С |
р кг/м |
Т,°С |
р кг/м |
Т, °С |
р кг/м |
|
-10 |
998,15 |
10 |
999,73 |
200 |
869,00 |
|
-5 |
999,30 |
20 |
998,23 |
250 |
794,00 |
|
0 |
999,87 |
50 |
988,07 |
300 |
710,00 |
|
2 |
999,97 |
100 |
958,38 |
350 |
574,00 |
|
4 |
1000,00 |
150 |
917,30 |
374,15 |
307,00 |
Плотность капельных жидкостей в зависимости от давления может быть определена в соответствии с уравнением состояния упругой жидкости:
![]() 5
5
• где: -
плотность капельной жидкости при
атмосферном давлении рат
,![]()
- коэффициент объёмного сжатия капельной жидкости.
Плотность идеальных газов при давлениях отличных от атмосферного можно определить по известному закону газового состояния Менделеева-Клайперона:
![]()
давление,
удельный объём газа,
универсальная газовая постоянная,
температура газа
при![]()
Кроме
абсолютной величины плотности капельной
жидкости, на практике пользуются и
величиной её относительной плотности,
которая представляет собой отношение
величины абсолютной плотности жидкости
к плотности чистой воды при температуре
4 °С: 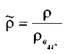 .
Относительная плотность жидкости -
величина безразмерная.
.
Относительная плотность жидкости -
величина безразмерная.
Имеется аналогичная характеристика и для газов. Под относительной плотностью газа (по воздуху) понимается отношение величины абсолютной плотности газа к плотности воздуха при стандартных условиях.
О
плотности жидкости косвенно можно
судить по весовому показателю, - удельному
весу жидкости. Под удельным весом
жидкости (газа) понимается вес единицы
объёма жидкости (газа):
где:G-вес жидкости (газа),
W-объем, занимаемый жидкостью (газом).
Связь между плотностью и удельным весом жидкости такая же как и между массой тела и её весом:
![]()
Размерность
удельного веса жидкости в системе единиц
СИ н/м
3 , удельный
вес чистой воды составляет
9810 н/м3. Аналогично
вводится понятие об относительном
удельном весе жидкости,![]()
На практике величина плотности жидкости определяется с помощью простейшего прибора - ареометра. По глубине погружения прибора в жидкость судят о её плотности.
Упругость. Капельные жидкости относятся к категории плохо сжимаемых тел. Причины незначительных изменений объёма жидкости при увеличении давления очевидны, т.к. межмолекулярные расстояния в капельной жидкости малы и при деформации жидкости приходится преодолевать значительные силы отталкивания, действующие между молекулами, и даже испытывать влияние сил, действующих внутри атома. Тем не менее, сжимаемость жидкостей в 5 - 10 раз выше, чем сжимаемость твёрдых тел, т.е. можно считать, что все капельные жидкости обладают упругими свойствами.
Оценка упругих свойств жидкостей может осуществляться по ряду специальных параметров.
![]() -коэффициент
объёмного сжатия жидкости представляет
собой относительное изменение объёма
жидкости при изменении давления на
единицу. По существу это известный
закон Гука для модели объёмного сжатия:
-коэффициент
объёмного сжатия жидкости представляет
собой относительное изменение объёма
жидкости при изменении давления на
единицу. По существу это известный
закон Гука для модели объёмного сжатия:
начальный
объём жидкости, (при начальном давлении),![]()
коэффициент объёмного (упругого) сжатия жидкости.
Считается, что коэффициент объёмного сжатия жидкости зависит с достаточно большой точностью только от свойств самой жидкости и не зависит от внешних условий. Коэффициент объёмного сжатия жидкости имеет размерность обратную размерности давления, т.е. м/н.
![]() -адиабатический
модуль упругости жидкости К, зависящий
от термодинамического состояния
жидкости (величина обратная коэффициенту
объёмного сжатия
жидкости):
-адиабатический
модуль упругости жидкости К, зависящий
от термодинамического состояния
жидкости (величина обратная коэффициенту
объёмного сжатия
жидкости):
Величина модуля упругости жидкости имеет размерность напряжения, т.е. н/м . об упругих свойствах капельной жидкости можно судить по скорости распространения продольных волн в жидкой среде, которая равна скорости звука в покоящейся жидкости:

С упругими свойствами капельных жидкостей также связаны представления о сопротивлении жидкостей растяжению. Теоретически в чистых жидкостях могут быть достигнуты довольно значительные напряжения. Однако, в реальных жидкостях при наличии в них даже весьма незначительных примесей (твёрдые частицы, газ) уменьшает величину сопротивления жидкости растяжению практически до 0. По этой причине можно считать, что в капельных жидкостях напряжения растяжению невозможны.
Об упругих свойствах газов можно судить исходя из классического уравнения Пуассона:
 ;
;
где: п - показатель адиабаты равный отношению теплоёмкости газа при постоянном давлении к величине теплоёмкости газа при постоянном объёме.

Для оценки упругих свойств движущегося газа пользуются не абсолютной величиной скорости звука сзв, а отношением скорости потока газа v к скорости звука в газе. Этот показатель носит название числа Маха;
![]()
Вязкость. При
движении реальных (вязких) жидкостей в
них возникают внутренние напряжения,
обусловленные силами внутреннего трения
жидкости. Природа этих сил довольно
сложна; возникающие в жидкости напряжения
связаны с процессом переноса
импульса![]() (вектора
массовой скорости движения жидкости).
При этом возникающие в жидкости напряжения
обусловлены двумя факторами: напряжениями,
возникающими при деформации сдвига и
напряжениями, возникающими при деформации
объёмного сжатия.
(вектора
массовой скорости движения жидкости).
При этом возникающие в жидкости напряжения
обусловлены двумя факторами: напряжениями,
возникающими при деформации сдвига и
напряжениями, возникающими при деформации
объёмного сжатия.
Наличие сил вязкостного трения в движущейся жидкости подтверждается простым и наглядным опытом. Если в цилиндрическую ёмкость, заполненную жидкостью опустить вращающийся цилиндр, то вскоре придёт в движение (начнёт вращаться вокруг своей оси в том же направлении, что и вращающийся цилиндр) и сама ёмкость с жидкостью. Этот факт свидетельствует о том, что вращательный момент от вращающегося цилиндра был передан через вязкую жидкость самой ёмкости, заполненной жидкостью.
Напряжения, возникающие при деформации сдвига согласно гипотезе Ньютона пропорциональны градиенту скорости в движущихся слоях жидкости, а сила трения между слоями движущейся жидкости будет пропорциональна площади поверхности движущихся слоев жидкости:
![]()
где:сила трения между слоями движущейся жидкости,
- площадь поверхности слоев движущейся жидкости,
 -
касательные напряжения, возникающие в
жидкости при деформации сдвига,
-
касательные напряжения, возникающие в
жидкости при деформации сдвига,
![]() коэффициент
динамической вязкости жидкости.
коэффициент
динамической вязкости жидкости.
Величина коэффициента динамической вязкости жидкости при постоянной температуре и постоянном давлении зависит от внутренних (химических) свойств самой жидкости. Размерность коэффициента динамической вязкости в системе единиц СИ: н с/м 2, в системе СГС - д-с/см . Последняя размерность носит название пуаза (пз). Таким образом, \пз =1 д-с/см , а соотношение между единицами вязкости. 1да=0,1 н с/м 2.
Помимо коэффициента динамической вязкости жидкости широко используется коэффициент кинематической вязкости жидкости v, представляющий собой отношение коэффициента динамической вязкости к плотности жидкости:
![]()
В системе единиц СИ коэффициент кинематической вязкости измеряется в м /с, в системе единиц СГС единицей измерения коэффициента кинематической вязкости жидкости является стоке (cm), т.е. 1 cm = 1 см /с.
Коэффициент динамической вязкости чистой воды составляет 1-10~3 н-с/м (или 0,01 пз),коэффициент кинематической вязкости чистой воды составляет МО" м /с (или 0,01 cm). - -
Коэффициенты вязкости жидкостей варьируют в весьма широких пределах от 0,0003 доО,139н-с/л/2.
Вязкость жидкости в значительной степени зависит от температуры и давления. При увеличении температуры капельной жидкости коэффициенты её вязкости (как динамический, так и кинематический) резко снижается в десятки и сотни раз, что обусловлено увеличением внутренней энергии молекул жидкости по сравнению с энергией межмолекулярной связи в жидкости.
Зависимость вязкости капельной жидкости от температуры может быть выражена в виде экспоненциальной зависимости:
![]()
где: - вязкость капельной жидкости при стандартной температуре TQ - 20 °С,
![]() - экспериментальный
температурный коэффициент. Зависимость
вязкости жидкости от давления в широком
диапазоне давлений остаётся практически
линейной:
- экспериментальный
температурный коэффициент. Зависимость
вязкости жидкости от давления в широком
диапазоне давлений остаётся практически
линейной:
![]()
где: ![]() -
вязкость жидкости при атмосферном
давлении,ар
- экспериментальный
-
вязкость жидкости при атмосферном
давлении,ар
- экспериментальный
коэффициент пропорциональности.
Газы обладают несравнимо более низкими коэффициентами вязкости от 0,0000084 до 0,0000192 н-с/м 2, и в отличие от капельных жидкостей вязкость газов увеличивается при увеличении температуры, т.к. с увеличением температуры газа возрастают скорости теплового движения молекул и, соответственно, увеличивается число соударений молекул газа, что делает газ более вязким. Зависимость вязкости газа от давления ничем не отличается от аналогичной зависимости для капельных жидкостей.
|
Коэффициент динамической вязкости жидкостей и газов |
| |||||||||||
|
Капельные жидкости приГ=18°С |
|
Газы при Т= 0 °С |
|
| ||||||||
|
Анилин |
0,00460 |
Азот |
0,0000167 |
| ||||||||
|
Ацетон |
, 0,00034 |
Аммиак |
0,0000093 | |||||||||
|
Бром -.-. • |
0,00102 |
Водород |
0,0000084 | |||||||||
|
Вода |
.* 0,00105 |
Воздух |
0,0000172 | |||||||||
|
Глицерин |
1,39300 |
Кислород |
0,0000192 | |||||||||
|
Масло машинное |
0,11300 |
Метан |
0,0000104 | |||||||||
|
Нефть |
0,0080-0,1000 |
Углекислота COi |
0,0000140 | |||||||||
|
Спирт этиловый |
0,00122 |
Хлор |
0,0000129 | |||||||||
|
|
|
|
|
|
|
|
| |||||
Измерение вязкости жидкостей осуществляется с помощью вискозиметров, работающих на принципе истечения жидкости через малое калиброванное отверстие; вязкость вычисляется по скорости истечения.
Кроме деформации сдвига внутреннее сопротивление в жидкости возникает и при объёмном сжатии жидкости, т.е. сжимаемая жидкость стремится восстановить состояние первоначального равновесия. Этот процесс, в некоторой степени, аналогичен проявлению сил сопротивления при деформации сдвига, хотя сам процесс и отличается по своей сути. По этой причине говорят, что в жидкости проявляется так называемая вторая вязкость £, обусловленная деформацией объёмного сжатия жидкости.
Поверхностное натяжение. Когда мы говорим о жидкости как о сплошной среде, это вовсе не означает, что эта среда бесконечна и безгранична. Жидкое тело всегда имеет границы, это либо твёрдые стенки каналов, либо границы раздела с газообразной средой, либо это граница раздела между различными несмешивающимися жидкостями. Такие границы можно с полным правом называть естественными границами.
В некоторых случаях границы могут выделяться условно внутри самой движущейся жидкости. На естественных границах в пограничном слое жидкости между молекулами самой жидкости и молекулами окружающей жидкость среды существуют силы притяжения, которые, в общем случае, могут оказаться не равными. В то же время силы взаимодействия между остальными молекулами жидкости, находящимися внутри объёма, ограниченного пограничным слоем эти силы взаимно уравновешены. Таким образом, остаются не уравновешенными силы взаимодействия между молекулами, находящимися лишь во внешнем (пограничном слое). Тогда в пограничном слое возникают напряжения, которые автоматически балансируют не сбалансированные силы притяжения. Такие напряжения называются поверхностным натяжением жидкости.
Этому напряжению будут соответствовать силы поверхностного натяжения. Под действием этих сил малые объёмы жидкости принимают сферическую форму (форму капли), соответствующей минимуму внутренней энергии; в трубках малого диаметра жидкость поднимается (или опускается) на некоторую высоту по отношению к уровню покоящейся жидкости. Последнее явление носит название капиллярности. Жидкость в трубке малого диаметра (капилляре) будет подниматься, если жидкость по отношению к стенке капилляра будет смачивающей жидкостью, и наоборот, будет опускаться, если жидкость для стенки капилляра окажется не смачивающей. Высоту h подъёма (опускания) жидкости в капилляре с диаметром d можно определить из соотношения:
![]() где: А
- постоянная
зависящая от свойств жидкости.
где: А
- постоянная
зависящая от свойств жидкости.
Для воды,
Для
ртути  ,
мм.
,
мм.
Силы поверхностного натяжения малы и проявляются при малых объёмах жидкости. Величина напряжений на границе раздела зависит от температуры жидкости; при увеличении температуры внутренняя энергия молекул возрастает и, естественно, уменьшается напряжение в пограничном слое жидкости и, следовательно, уменьшаются силы поверхностного натяжения.
Растворимость
газов в капельных жидкостях. В
реальных жидкостях всегда находится
в растворённом состоянии газ. Это может
быть воздух, азот, углеводородный газ,
углекислота![]() сероводороди
сероводороди![]() др.
Наличие газа растворённого в жидкости
может оказывать как благоприятное
воздействие (снижается вязкость жидкости,
плотность и т.д.), так и неблагоприятные
факторы. Так при снижении давления из
жидкости выделяется свободный газ,
который может стать источником такого
нежелательного явления как кавитация;
выделяющийся газ может оказаться не
безопасным для окружающей среды (HiS),
огнеопасным и взрывоопасным (углеводородный
газ). Газ, растворённый в жидкости,
как и газ в свободном состоянии может
также способствовать коррозии стенок
труб и оборудования, вызывать химические
реакции, ведущие к образованию отложений
твёрдых солей на стенках труб, накипей
и др. По этой причине знание особенностей
и законов растворения газа в жидкости
крайне желательно.
др.
Наличие газа растворённого в жидкости
может оказывать как благоприятное
воздействие (снижается вязкость жидкости,
плотность и т.д.), так и неблагоприятные
факторы. Так при снижении давления из
жидкости выделяется свободный газ,
который может стать источником такого
нежелательного явления как кавитация;
выделяющийся газ может оказаться не
безопасным для окружающей среды (HiS),
огнеопасным и взрывоопасным (углеводородный
газ). Газ, растворённый в жидкости,
как и газ в свободном состоянии может
также способствовать коррозии стенок
труб и оборудования, вызывать химические
реакции, ведущие к образованию отложений
твёрдых солей на стенках труб, накипей
и др. По этой причине знание особенностей
и законов растворения газа в жидкости
крайне желательно.
Количество газа, которое может раствориться в капельной жидкости, зависит от физико-химических свойств самой жидкости и растворяемого в ней газа, а также от температуры и давления. Максимальное количество газа, которое может быть растворено в данной жидкости носит название предельной газонасыщенности для данного газа s0. Естественно, что величины предельной газонасыщенности для разных газов будут разными. Другой характеристикой процесса растворения газа в жидкости является давление насычении температуры внутренняя энергия молекул возрастает и, естественно, уменьшается напряжение в пограничном слое жидкости и, следовательно, уменьшаются силы поверхностного натяжения.
Растворимость
газов в капельных жидкостях. В
реальных жидкостях всегда находится
в растворённом состоянии газ. Это может
быть воздух, азот, углеводородный газ,
углекислота![]() ,
сероводород HiS и др. Наличие газа
растворённого в жидкости может оказывать
как благоприятное воздействие (снижается
вязкость жидкости, плотность и т.д.), так
и неблагоприятные факторы. Так при
снижении давления из жидкости выделяется
свободный газ, который может стать
источником такого нежелательного
явления как кавитация; выделяющийся
газ может оказаться не безопасным для
окружающей среды
,
сероводород HiS и др. Наличие газа
растворённого в жидкости может оказывать
как благоприятное воздействие (снижается
вязкость жидкости, плотность и т.д.), так
и неблагоприятные факторы. Так при
снижении давления из жидкости выделяется
свободный газ, который может стать
источником такого нежелательного
явления как кавитация; выделяющийся
газ может оказаться не безопасным для
окружающей среды![]() ,
огнеопасным и взрывоопасным (углеводородный
газ). Газ, растворённый в жидкости,
как и газ в свободном состоянии может
также способствовать коррозии стенок
труб и оборудования, вызывать химические
реакции, ведущие к образованию отложений
твёрдых солей на стенках труб, накипей
и др. По этой причине знание особенностей
и законов растворения газа в жидкости
крайне желательно.
,
огнеопасным и взрывоопасным (углеводородный
газ). Газ, растворённый в жидкости,
как и газ в свободном состоянии может
также способствовать коррозии стенок
труб и оборудования, вызывать химические
реакции, ведущие к образованию отложений
твёрдых солей на стенках труб, накипей
и др. По этой причине знание особенностей
и законов растворения газа в жидкости
крайне желательно.
Количество
газа, которое может раствориться в
капельной жидкости, зависит от
физико-химических свойств самой
жидкости и растворяемого в ней газа, а
также от температуры и давления.
Максимальное количество газа, которое
может быть растворено в данной
жидкости носит название предельной
газонасыщенности для данного газа s0.
Естественно, что величины предельной
газонасыщенности для разных газов будут
разными. Другой характеристикой процесса
растворения газа в жидкости является
давление насыщения ![]() ,
это такое минимальное давление в
жидкости, при котором достигается
насыщение капельной жидкости газом.
При невысоких давлениях значительно
уступающих величине давления насыщения
справедлив закон растворимости Генри:
,
это такое минимальное давление в
жидкости, при котором достигается
насыщение капельной жидкости газом.
При невысоких давлениях значительно
уступающих величине давления насыщения
справедлив закон растворимости Генри:
![]()
Количество газа растворимого в единице объёма жидкости пропорционально давлению. При увеличении давления до давления насыщения

Кривая
растворимости газа в
жидкости s(p). коэффициента
растворимости газа![]()
— давление насыщения, sn — величина
![]() снижается,
пропорционально газонасыщенности
снижается,
пропорционально газонасыщенности
В жидкости может одновременно растворяться целая группа различных газов; нередки случаи, когда капельная жидкость и растворяемый в ней газ имеют одинаковую природу (нефть и углеводородные газы); в последнем случае между жидкостью и газом может существовать весьма условная граница, зависящая от температуры смеси и других прочих условий.
Испаряемость. При повышении температуры жидкости и, в некоторых случаях, при снижении давления часть массы капельной жидкости постепенно переходит в газообразное состояние (пар). Интенсивность процесса парообразования зависит от температуры кипения жидкости при нормальном атмосферном давлении: чем выше температура кипения жидкости, тем меньше её испаряемость. Однако, более полной характеристикой испаряемости следует считать давление (упругость) насыщенных паров, данное в функции температуры. Чем больше насыщенность паров при данной температуре, тем больше испаряемость жидкости.
Адсорбция Адсорбцией принято называть концентрацию одного из веществ, происходящую в его поверхностном слое, т.е. на границе раздела двух фаз (например, жидкость и поверхность твёрдого тела). Такая концентрация молекул жидкости на поверхности твёрдого тела обуславливается силами межмолекулярного взаимодействия. Так сила притяжения молекул жидкости со стороны молекул твёрдого тела неизмеримо выше, силы притяжения оказываемой со стороны молекул самой жидкости. По этой причине на поверхности твёрдого тела образуется устойчивая пленка, состоящая из молекул жидкости, которая способна удерживаться на поверхности твёрдого тела даже в том случае, когда вдоль поверхности твёрдого тала перемещается поток жидкости. Сильное притяжение со стороны молекул твёрдого тела могут испытывать также и молекулы второго и третьего слоев молекул жидкости, т.е. образующаяся на поверхности твердого тела плёнка из частиц жидкости может быть многослойной. Поскольку сила взаимодействия между молекулами убывает с увеличением расстояния между ними, то молекулы удалённых от поверхности твёрдого тела слоев легко разрушаются под действием различных сил, т.е. внешние слои молекул жидкости крайне неустойчивы. Процесс разрушения образованной плёнки из жидких молекул называется десорбцией. Как правило, эти два процесса идут одновременно, образуя состояние неустойчивого равновесия.
Адсорбируемое вещество (в нашем случае это жидкость) называется адсорбатом, а адсорбирующее вещество (в нашем случае это твёрдое тело) называется адсорбентом. Процесс собственно адсорбции происходит на поверхности твёрдого тела без внедрения молекул адсорбата в твёрдое тело.
В тех случаях, когда молекулы адсорбата проникают в поверхностный слой адсорбента, то такой процесс приято называть абсорбцией. Если же при этом будет происходить химические реакции между веществами, то такой процесс носит название хемсорбции. Следует отметить, что скорость сорбционных процессов зависит от внешних условий (температура и давление) а также от свойств самих веществ. На практике с сорбционными процессами мы встречаемся при гидроизоляции зданий и сооружений, при уплотнении сальников в различных механизмах и машинах.
Чтобы представить и правильно понять характер поведения жидкости в различных условиях необходимо обратиться к некоторым представлениям классической физики о жидкости как физическом теле. Не ставя перед собой цель детального и всестороннего описания жидких тел, что подробно рассматривается в классическом курсе физики, напомним лишь некоторые положения, которые могут пригодиться при изучении гидравлики как самостоятельной дисциплины.
Так, согласно молекулярно-кинетической теории строения вещества все физические тела в природе (независимо от их размеров) находятся в постоянном взаимодействии между собой. Степень (интенсивность) взаимодействия зависит от масс этих тел и от расстояния между телами. Количественной мерой взаимодействия тел является сила, которая пропорциональна массе тел и всегда будет убывать при увеличении расстояния между телами. В зависимости от размеров тел (элементарные частицы, атомы и молекулы, макротела) характер взаимодействия будет различным. Согласно классическим представлениям физики можно выделить четыре вида взаимодействия тел. Каждый вид взаимодействия обусловлен наличием своего переносчика взаимодействия. Два вида взаимодействия относятся к типу дальнодействующих и повседневно наблюдаются человеком: гравитационное и электромагнитное. При электромагнитном взаимодействии происходит процесс излучения и поглощения фотонов. Именно этот процесс порождает электромагнитные силы, под действием которых протекают практически все процессы в природе, которые мы наблюдаем. Характерной особенностью этого (электромагнитного) взаимодействия является то, что его проявление зависит от многих внешних условий, которые приводят к различным наблюдаемым результатам. Так имея одну и туже природу взаимодействия (электромагнитную) мы изучаем, на первый взгляд, совершенно разные физические процессы: движение жидкости, трение, упругость, передачу тепла, движение зарядов в электрическом поле и т.д. И, как следствие, дифференциальные уравнения, описывающие эти процессы, одинаковые.
Согласно молекулярно-кинетической теории строения вещества молекулы находятся в равновесии и, как материальные объекты постоянно взаимодействуют друг с другом. Такое равновесие нельзя считать абсолютным, т.к. молекулы находятся в состоянии хаотического движения (колебания) вокруг центра своего равновесия. Расстояния между молекулами вещества будет зависеть от величин сил действующих на молекулы. Независимо от природы действующих сил их можно сгруппировать на силы притяжения и силы отталкивания.
Условие равновесия этих сил определяет оптимальные расстояния между молекулами. Однако, в связи с тем, что такое равновесие между действующими силами является динамическим равновесием, молекулы находятся в постоянном колебательном движении относительно друг друга, испытывая при этом действие некоторой равнодействующей силы порождаемой силами притяжения и отталкивания. Поэтому особенности состояния вещества будут зависеть от соотношения между кинетической энергией колебательного движения молекул вещества и энергией взаимодействия между молекулами вещества. Так при больших массах молекул энергия взаимодействия между молекулами многократно превышает кинетическую энергию колебательного движения вещества, вследствие чего молекулы вещества занимают устойчивое положение относительно друг друга, обеспечивая тем самым постоянство формы и размеров макротела. Такие вещества, как известно, относятся к категории твёрдых тел. Противоположными особенностями характеризуются вещества, состоящие из «лёгких» молекул (молекул обладающих малой массой). Такие вещества обладают кинетической энергией колебательного движения молекул вещества превышающей многократно энергию взаимодействия между молекулами, из которых вещество состоит. По этой причине молекулы такого вещества имеют очень слабую связь между собой и легко перемещаются в пространстве на любые расстояния. Такое свойство вещества носит название диффузии (летучести). Вещества, обладающие эти свойством, относятся к категории газов. В тех случаях, когда энергия взаимодействия имеет тот же порядок, что и величина кинетической энергии колебательного движения молекул, последние обладают свойством относительной подвижности, но, при этом, сохраняют целостность самого макротела. Такое тело обладает способностью легко деформироваться при минимальных касательных напряжениях, т. е. такое тело обладает текучестью. На самом деле колебательный процесс среди молекул жидких тел достаточно сложен, и с целью простого описания данного процесса можно нарисовать упрощенную картину взаимодействия молекул жидкости. Так в отличие от молекул в твёрдых телах, при колебательном процессе в жидкости центры взаимодействия молекул могут смещаться в пространстве на столько, на сколько это допускают расстояния между молекулами (до величины 1x10 " см). Смещение центра равновесия сил в пространстве называется релаксацией. Время, за которое происходит такое смещение, называется временем релаксации, t0. При этом смещение центра равновесия осуществляется не постепенно, а скачком. Таким образом, время релаксации характеризует продолжительность «оседлой жизни» молекул жидкости. Если на жидкость будет действовать некоторая сила F, то при совпадении линии действия этой силы с направлением скачка, жидкость начнёт перемещаться. При этом необходимо выполнение дополнительного условия: продолжительность действия силы должна быть больше длительности времени релаксации t0, т.к. в противном случае жидкость не успеет начать своё движение, и будет испытывать упругое сжатие подобно твёрдому телу. Тогда процесс движения жидкости будет характеризовать свойство текучести присущее практически только жидким телам. Тела с такими свойствами относятся к категории жидких тел.
При этом следует отметить, что чётких и жёстких границ между твёрдыми, жидкими и газообразными телами нет. Имеется большая группа тел занимающих промежуточное положение между твёрдыми телами и жидкостями и между жидкостями и газами. Вообще говорить о состоянии вещества можно только при вполне определённых внешних условиях. В качестве стандартных условий приняты условия при температуре 20 °С и атмосферном давлении. Стандартные (нормальные) условия вполне соотносятся с понятием благоприятных внешних условий для существования человека. Понятие о состоянии вещества необходимо дополнить. Так при увеличении кинетической энергии молекул вещества (нагрев вещества) твёрдые тела могут перейти в жидкое состояние (плавление твёрдого тела) и твёрдые тела приобретут при этом некоторые свойства жидкостей. Подобно этому увеличение кинетической энергии молекул жидкого вещества может привести жидкость в газообразное состояние (парообразование) и при этом жидкость будет иметь свойства соответствующие газам. Аналогичным способом можно превратить расплавленное твёрдое тело в пар, если в большей степени увеличить кинетическую энергию колебательного движения молекул первоначально твёрдого вещества. Уменьшение кинетической энергии молекул (охлаждение вещества) приведёт процесс в обратном направлении. Газ может быть превращён в жидкое, а, затем и в твёрдое состояние
Изучение реальных жидкостей и газов связано со значительными трудностями, т.к. физические свойства реальных жидкостей зависят от их состава, от различных компонентов, которые могут образовывать с жидкостью различные смеси как гомогенные (растворы) так и гетерогенные (эмульсии, суспензии и др.) По этой причине для вывода основных уравнений движения жидкости приходится пользоваться некоторыми абстрактными моделями жидкостей и газов, которые наделяются свойствами неприсущими природным жидкостям и газам.
Идеальная жидкость - модель природной жидкости, характеризующаяся изотропностью всех физических свойств и, кроме того, характеризуется абсолютной несжимаемостью, абсолютной текучестью (отсутствие сил внутреннего трения), отсутствием процессов теплопроводности и теплопереноса.
Реальная жидкость - модель природной жидкости, характеризующаяся изотропностью всех физических свойств, но в отличие от идеальной модели, обладает внутренним трением при движении.
Идеальный газ - модель, характеризующаяся изотропностью всех физических свойств и абсолютной сжимаемостью.
Реальный газ - модель, при которой на сжимаемость газа при условиях близких к нормальным условиям существенно влияют силы взаимодействия между молекулами.
При изучении движения жидкостей и газов теоретическая гидравлика (гидромеханика) широко пользуется представлением о жидкости как о сплошной среде. Такое допущение вполне оправдано, если учесть, что размеры пространства занимаемого жидкостью, во много раз превосходят межмолекулярные расстояния (исключением можно считать лишь разряженный газ). При изучении движения жидкостей и газов последние часто рассматриваются как жидкости с присущими им некоторыми особыми свойствами. Всвязи с этим принято различать две категории жидкостей: капельные жидкости (практически несжимаемые тела, или собственно жидкости) и сжимаемые жидкости (газы).
Вопрос №3. Силы, действующие в жидкости. Гидростатическое давление.
Поскольку жидкость обладает свойством текучести и легко деформируется под действием минимальных сил, то в жидкости не могут действовать сосредоточенные силы, а возможно существование лишь сил распределённых по объёму (массе) или по поверхности. В связи с этим действующие на жидкости распределённые силы являются по отношению к жидкости внешними. По характеру действия силы можно разделить на две категории: массовые силы и поверхностные.
Массовые силы пропорциональны массе тела и действуют на каждую жидкую частицу этой жидкости. К категории массовых сил относятся силы тяжести и силы инерции переносного движения. Величина массовых сил, отнесённая к единице массы жидкости, носит название единичной массовой силы. Таким образом, в данном случае понятие о единичной массовой силе совпадает с определением ускорения. Если жидкость, находится под действием только сил тяжести, то единичной силой является ускорение свободного падения:

где М' - масса жидкости
Если жидкость находится в сосуде, движущимся с некоторым ускорением а, то жидкость в сосуде будет обладать таким же ускорением (ускорением переносного движения):
![]()
Поверхностные силы равномерно распределены по поверхности и пропорциональны площади этой поверхности. Эти силы, действуют со стороны соседних объёмов жидкой среды, твёрдых тел или газовой среды. В общем случае поверхностные силы имеют две составляющие нормальную и тангенциальную. Единичная поверхностная сила называется напряжением. Нормальная составляющая поверхностных сил называется силой давления Р, а напряжение (единичная сила) называется давлением:
![]()
где: S - площадь поверхности.
Напряжение
тангенциальной составляющей поверхностной
силы Т (касательное
напряжение![]() )
определяется аналогичным образом (в
покоящейся жидкости Т=0).
)
определяется аналогичным образом (в
покоящейся жидкости Т=0).
![]()
Величина давления (иногда в литературе называется гидростатическим давлением) в системе СИ измеряется в паскалях.
![]()
Поскольку эта величина очень мала, то величину давления принято измерять в мега-паскалях МПа
1МПа = \ 106 Па.
В употребляемой до сих пор технической системе единиц давление измеряется в технических атмосферах, am. С,
1 am = \кГ/см2 = 0,1 МПа, 1 МПа = 10 am.
В технической системе единиц давление кроме технической атмосферы измеряется также в физических атмосферах, А.
\А = 1,033 am.
Различают давление абсолютное, избыточное и давление вакуума. Абсолютным давлением называется давление в точке измерения, отсчитанное от нуля. Если за уровень отсчёта принята величина атмосферного давления, то разница между абсолютным давлением и атмосферным называется избыточным давлением.
![]()
Если давление, измеряемое в точке ниже величины атмосферного давления, то разница между замеренным давлением и атмосферным называется давлением вакуума
![]()
Избыточное давление в жидкостях измеряется манометрами. Это весьма обширный набор измерительных приборов различной конструкции и различного исполнения.
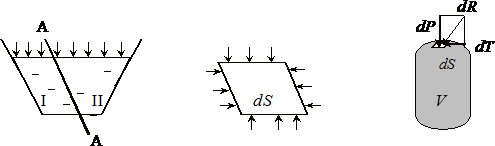
Рассечем жидкость, находящуюся в объеме V (например, сосуде) некоторой поверхностью на две части I и II ( рис. 15 ).
а б в
Рис. 15
Рассмотрим жидкость в объеме I. Все, что окружает этот объем, отбросим (дно, боковые стенки и т.д.) и действие отброшенного объема жидкости заменим соответствующими силами. Эти силы называютсяповерхностными.
Кроме них на жидкость действуют еще массовые силы (силы тяжести и инерции), которые пропорциональны массе тела.
Выделим из жидкости некоторый объем. Возьмем на поверхности этого объема бесконечно малую площадку dS. Hа эту площадку действует поверхностная сила dR. Разложим эту силу на нормальную dP и касательную dT.
Hормальная сила, приходящаяся на единицу площади, называется давлением и обозначается буквой p, т.е.
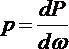 .
.
В
системе СИ давление измеряется в ![]() .
.
|
Рис. 16 |
Сила трения (касательная сила), приходящаяся на единицу площади, обозначается буквой t, т.е.
Сила
трения обычно пропорциональна градиенту
скорости |
Для
жидкости, находящейся в равновесии (в
покое), сила трения равна нулю, так как
в этом случае .
.
Вопрос №4. Уравнение равновесия жидкости (уравнение Эйлера).
Запишем уравнение Эйлера
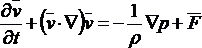 .
.
Если жидкость покоится
![]() .
.
Дифференциальные уравнения равновесия жидкости в проекции на оси декартовой системы координат могут быть записаны так
 .
.
Здесь Fx, Fy, Fz - проекции на оси x,y,z сил, действующих на единицу массы рассматриваемой жидкости.
Умножая давления соответственно на dxdydz и складывая их, получаем
 .
.
Левая часть уравнения представляет полный дифференциал
![]() ,
,
следовательно, и правая часть должна быть также полным дифференциалом, для этого необходимо и достаточно, при постоянном r, чтобы существовала функция U(x,y,z) такая что
 ,
,  ,
,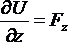 .
.
Имеем
![]() .
.
Проинтегрировав, получим
![]() ,
,
где С - постоянная интегрирования.
Если в какой-либо точке известно давление po и постоянная функция Uo, то
![]() ,
,
из интеграла имеем
![]() .
.
В частности, когда жидкость находится в поле сил тяжести
![]() ,
, ![]() ,
,![]() .
.
Следовательно,

Уравнение для давления принимает вид
![]() .
.
Свободная поверхность жидкости плоская z=const. При равновесии жидкости в поле земного тяготения поверхности уровня представляют собой горизонтальные плоскости.
Рассмотрим примеры.
Пример 1. Определить уравнение свободной поверхности жидкости в сосуде, движущемся горизонтально с ускорением а.
Решение. На жидкость действуют сила тяжести и сила инерции, т.е.
![]() ,
, ![]() ,
,![]() .
.
|
|
Имеем
откуда
- уравнение прямой. |
Следовательно,
свободная поверхность представляет
собой плоскость, наклоненную к горизонту
под углом ![]() ,
который определяется из равенства
,
который определяется из равенства
 .
.
Пример 2. Определить уравнение свободной поверхности жидкости в сосуде, вращающемся вокруг вертикальной оси с угловой скоростью w .
Решение. Вследствие трения о стенки сосуда жидкость будет вращаться с такой же угловой скоростью. Жидкость будет находиться в относительном покое. Поэтому при решении задачи применимы уравнения равновесия.
|
|
Из массовых сил на жидкость действует центробежная сила и сила тяжести. Центробежная сила, действующая на массу m, находится на расстоянии r от оси вращения ( рис. 18 )
Проекции силы на оси, отнесенные к единице массы, будут
Тогда
|
Откуда
 ,
,
т.е. свободная поверхность - параболоид вращения.
Вопрос №5. Абсолютное, избыточное давление. Вакуум. Приборы для измерения давления.
Приборами для измерения барометрического давления служат барометры различных конструкций.
Для измерения манометрического давления служит манометр. Манометрическое давление можно измерить высотой столба жидкости. Сосуд наполнен жидкостью с плотностью r. Давление на свободной поверхности po>рб.
Пусть необходимо измерить давление на уровне 1-1. Если на этом уровне сделать отверстие и присоединить к нему стеклянную трубку П, то жидкость в этой трубе поднимется под действием давления на некоторую высоту h.
|
|
По основному уравнению гидростатики
откуда
Этой высотой h поднятия жидкости в трубке П можно измерять манометрическое давление ( рис. 19 ). Трубка П называется пьезометром. |
Hайдем
соотношение между 1![]() ,
1м
вод. ст.
и 1 мм
рт. ст.
,
1м
вод. ст.
и 1 мм
рт. ст.
При высоте водного столба h=1 м давление
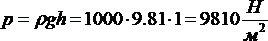 .
.
При высоте ртутного столба h = 1 мм давление
 .
.
Для
измерения вакуумметрического
давления
применяется вакуумметр.
Допустим, что требуется измерить
вакуумметрическое давление воздуха в
сосуде S,
т.е. величину ![]() ,
гдеpa -
абсолютное давление в сосуде.
,
гдеpa -
абсолютное давление в сосуде.
Присоединим к сосуду изогнутую трубку, опущенную в жидкость.
|
Рис. 20 |
Применяя основное уравнение гидростатики для точки, расположенной в трубке на уровне свободной поверхности жидкости в резервуаре ( рис. 20 ), получим
откуда
|
Так как
![]() ,
,
то
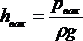 .
.
Вакуумметрическому
давлению будет соответствовать высота
подъема ![]() жидкости
в изогнутой трубке над уровнем в
резервуаре.
жидкости
в изогнутой трубке над уровнем в
резервуаре.
Различают следующие виды давления: барометрическое, абсолютное, манометрическое и вакуумметрическое.
Барометрическое (или
атмосферное) давление pб зависит
от места над уровнем моря и от погоды.
За нормальное барометрическое давление
принимают давление, равное 760 мм рт. ст.,
что соответствует 101325![]() С
высотой барометрическое давление
убывает. В глубоких шахтах барометрическое
давление значительно больше, чем на
уровне моря.
С
высотой барометрическое давление
убывает. В глубоких шахтах барометрическое
давление значительно больше, чем на
уровне моря.
Давление,
вычисляемое по соотношению ![]() ,
называется абсолютным.
,
называется абсолютным.
Абсолютное давление в точке равно сумме внешнего поверхностного и весового давления.
Если к свободной поверхности приложено барометрическое давление pб, то есть pб=ро и основное уравнение гидростатики перепишем так
![]() .
.
Давление ![]() носит
название манометрического или избыточного.
Таким образом, манометрическим давлением
называется разность между абсолютным
давлением pа и
барометрическим pб,
если pa>рб.
носит
название манометрического или избыточного.
Таким образом, манометрическим давлением
называется разность между абсолютным
давлением pа и
барометрическим pб,
если pa>рб.
Если в данной точке жидкости абсолютное давление меньше барометрического, то разность между барометрическим и абсолютным давлениями называется вакуумметрическим давлением.
Итак, если pa<рб, то
![]() .
.
Абсолютное
давление ![]() отрицательным
быть не может, поэтому вакуумметрическое
давление не может быть больше
барометрического.
отрицательным
быть не может, поэтому вакуумметрическое
давление не может быть больше
барометрического.
Вопрос №6. Сила давления жидкости на плоские поверхности, точка ее приложения.
Гидростатическое давление представляет собой систему параллельных сил, действующих в одну сторону и перпендикулярных к плоскости стенок (рис. 21).
|
Рис. 21 |
Такая система приводится к одной силе - равнодействующей, равной арифметической сумме всех сил и приложенной в центре параллельных сил. Для определения равнодействующей давлений, приложенных к площадке S, плоскость которой Q наклонена к горизонту под углом q, |
возьмем начало координат в плоскости приведенного уровня на линии пересечения с плоскостью площадки, приняв линию пересечения за ось oy1 и направив ось oz1 вертикально вниз, кроме того в плоскости площадки возьмем вспомогательные оси oy и ox, совместив oy1 и oy.
 ,
,
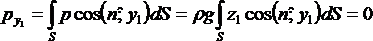 ,
,
 .
.
Откуда
 .
.
Последний интеграл равен площади площадки S, умноженной на координату центра тяжести z1c
![]() .
.
Произведение ![]() выражает
объем цилиндрического столба с основаниемS и
высотой z1c
и мы приходим к выводу, что
давление тяжелой жидкости на плоскую
площадку измеряется весом цилиндрического
столба этой жидкости, который был бы
расположен над площадкой, если бы она
лежала горизонтально на глубине своего
центра тяжести.
выражает
объем цилиндрического столба с основаниемS и
высотой z1c
и мы приходим к выводу, что
давление тяжелой жидкости на плоскую
площадку измеряется весом цилиндрического
столба этой жидкости, который был бы
расположен над площадкой, если бы она
лежала горизонтально на глубине своего
центра тяжести.
Сосуды различной формы, но с одинаковой площадью дна, наполненные жидкостью на одну и ту же высоту H, имеют одинаковую силу давления на дно ( рис. 22 ).

а б в
Рис. 22
Вопрос №7. Построение и использование эпюр давления.
Пусть мы имеем резервуар с наклонной правой стенкой, заполненный жидкостью с удельным весом γ. Ширина стенки в направлении, перпендикулярном плоскости чертежа (от читателя), равна b (рис.2.3). Стенка условно показана развернутой относительно оси АВ и заштрихована на рисунке. Построим график изменения избыточного гидростатического давления на стенку АВ.
Так как избыточное гидростатическое давление изменяется по линейному закон P=γgh, то для построения графика, называемого эпюрой давления, достаточно найти давление в двух точках, например А и B.

Рис. 2.3. Схема к определению равнодействующей гидростатического давления на плоскую поверхность
Избыточное гидростатическое давление в точке А будет равно
PA = γh = γ·0 = 0
Соответственно давление в точке В:
PB = γh = γH
где H - глубина жидкости в резервуаре.
Согласно первому свойству гидростатического давления, оно всегда направлено по нормали к ограждающей поверхности. Следовательно, гидростатическое давление в точке В, величина которого равна γH, надо направлять перпендикулярно к стенке АВ. Соединив точку А с концом отрезка γH, получим треугольную эпюру распределения давления АВС с прямым углом в точке В. Среднее значение давления будет равно
![]()
Если площадь наклонной стенки S=bL, то равнодействующая гидростатического давления равна
![]()
где hc = Н/2 - глубина погружения центра тяжести плоской поверхности под уровень жидкости.
Однако точка приложения равнодействующей гидростатического давления ц.д. не всегда будет совпадать с центром тяжести плоской поверхности. Эта точка находится на расстоянии l от центра тяжести и равна отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки.
![]()
где JАx - момент инерции площади S относительно центральной оси, параллельной Аx.
В частном случае, когда стенка имеет форму прямоугольника размерами bL и одна из его сторон лежит на свободной поверхности с атмосферным давлением, центр давления ц.д. находится на расстоянии b/3 от нижней стороны.
Эпюра давления жидкости — это графическое изображение распределения давления жидкости по твёрдой поверхности, соприкасающейся с жидкостью. Примеры эпюр для плоских и криволинейных поверхностей см. на рис. 5 и 6. Стрелками на эпюре показывают направление действия давления (вернее, направление нормальных напряжений, возникающих от действия давления, так как по 2-му свойству давление скалярно). Величина стрелки (ордината) откладывается в масштабе и количественно показывает величину давления.


Эпюры давления служат исходными данными для проведения расчётов на прочность и устойчивость конструкций, взаимодействующих с жидкостями: стенок плавательных бассейнов, баков, резервуаров, цистерн. Расчёты ведутся методами сопротивления материалов и строительной механики.
В большинстве расчётных случаев строят эпюры избыточного давления pизб вместо полного p, а атмосферное pатм не учитывают из-за его взаимного погашения с той и другой стороны ограждающей конструкции.
При построении таких эпюр для плоских и криволинейных поверхностей (см. рис. 5 и 6) используют линейную зависимость давления от глубины pизб = g h и 1-е свойство гидростатического давления
Вопрос №8. Определение силы гидростатического давления на криволинейную поверхность.
Пусть жидкость заполняет резервуар, правая стенка которого представляет собой цилиндрическую криволинейную поверхность АВС (рис.2.4), простирающуюся в направлении читателя на ширину b. Восстановим из точки А перпендикуляр АО к свободной поверхности жидкости. Объем жидкости в отсекеАОСВ находится в равновесии. Это значит, что силы, действующие на поверхности выделенного объема V, и силы веса взаимно уравновешиваются.
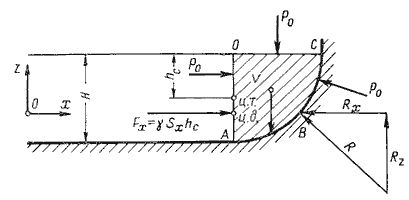
Рис. 2.4. Схема к определению равнодействующей гидростатического давления на цилиндрическую поверхность
Представим, что выделенный объем V представляет собой твердое тело того же удельного веса, что и жидкость (этот объем на рис.2.4 заштрихован). Левая поверхность этого объема (на чертеже вертикальная стенка АО) имеет площадь Sx = bH, являющуюся проекцией криволинейной поверхности АВС на плоскостьyOz.
Cила гидростатического давления на площадь Sx равна Fx = γ Sxhc.
С правой стороны на отсек будет действовать реакция R цилиндрической поверхности. Пусть точка приложения и направление этой реакции будут таковы, как показано на рис.2.4. Реакцию R разложим на две составляющие Rx и Rz.
Из действующих поверхностных сил осталось учесть только давление на свободной поверхности Р0. Если резервуар открыт, то естественно, что давление Р0 одинаково со всех сторон и поэтому взаимно уравновешивается.
На отсек АВСО будет действовать сила собственного веса G = γV, направленная вниз.
Спроецируем все силы на ось Ох:
Fx - Rx = 0 откуда Fx = Rx = γSxhc
Теперь спроецируем все силы на ось Оz:
Rx - G = 0 откуда Rx = G = γV
Составляющая силы гидростатического давления по оси Oy обращается в нуль, значит Ry = Fy = 0.
Таким образом, реакция цилиндрической поверхности в общем случае равна
![]()
а поскольку реакция цилиндрической поверхности равна равнодействующей гидростатического давленияR=F, то делаем вывод, что
![]()
Вопрос №9. Закон Архимеда.
Определим силу давления жидкости на погруженное тело А объемом W
|
|
Представим, что в жидкости выделен объем, точно такой же, как и тело А. Этот объем жидкости находится в равновесии под действием двух сил ( рис. 24 ) : 1) силы давления жидкости P на поверхность выделенного объема, 2) силы тяжести жидкости, равной rWg и направленной вертикально вниз. |
Следовательно, сила Р равна силе тяжести выделенного объема жидкости, направленная в обратную сторону, то есть вертикально вверх, и приложена в центре объема, т.е. в той же точке, в которой приложена сила тяжести выделенного объема жидкости.
Точка D называется центром водоизмещения.
Закон Архимеда. Сила давления жидкости на погруженное в нее тело приложена в центре водоизмещения, направлена вертикально вверх и равна силе тяжести жидкости, вытесненной телом
![]() .
.
Сила P называется архимедовой силой, W – объемным водоизмещением, а rW - водоизмещением.
Вопрос №10. Относительное давление жидкости в сосуде, движущемся прямолинейно с постоянным ускорением.
Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называется поверхностью уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.
Рассмотрим два примера такого относительного покоя.
В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по горизонтальному пути с постоянным ускорением a (рис.2.6).

Рис. 2.6. Движение цистерны с ускорением
К
каждой частице жидкости массы m должны
быть в этом случае приложены ее вес G
= mg и
сила инерцииPu,
равная по величине ma.
Равнодействующая ![]() этих
сил направлена к вертикали под углом
α, тангенс которого равен
этих
сил направлена к вертикали под углом
α, тангенс которого равен
![]()
Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным, направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону (см. рис.2.6, пунктир)
Вопрос №11. Относительное равновесие жидкости в сосуде, равномерно вращающемся вокруг вертикальной оси.
В качестве второго примера рассмотрим часто встречающийся в практике случай относительного покоя жидкости во вращающихся сосудах (например, в сепараторах и центрифугах, применяемых для разделения жидкостей). В этом случае (рис.2.7) на любую частицу жидкости при ее относительном равновесии действуют массовые силы: сила тяжести G = mg и центробежная сила Pu = mω2r, где r - расстояние частицы от оси вращения, а ω - угловая скорость вращения сосуда.

Рис. 2.7. Вращение сосуда с жидкостью
Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и представит собой параболоид вращения. Из чертежа находим
![]()
С другой стороны:
![]()
где z - координата рассматриваемой точки. Таким образом, получаем:
![]()
откуда
![]()
или после интегрирования
![]()
В точке пересечения кривой АОВ с осью вращения r = 0, z = h = C, поэтому окончательно будем иметь
![]()
т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом. Такую же форму имеют и другие поверхности уровня.
Для определения закона изменения давления во вращающейся жидкости в функции радиуса и высоты выделим вертикальный цилиндрический объем жидкости с основанием в виде элементарной горизонтальной площадки dS (точка М) на произвольном радиусе r и высоте z и запишем условие его равновесия в вертикальном направлении. С учетом уравнения (2.11) будем иметь

После сокращений получим
![]()
Это значит, что давление возрастает пропорционально радиусу r и уменьшается пропорционально высоте z.
Вопрос №12. Поверхности равных давлений. Гидростатический закон распределения давления.
Поверхность, во всех точках которой значения гидростатического давления равны между собой, называют поверхностью равного давления или поверхностью уровня. На положение уровня свободной поверхности влияют силы тяжести и инерции.
Найдем величину равного давления Р по трем частным производным. При Р=const и р # 0 значение полного дифференциала dP=0 и, следовательно, уравнение поверхности жидкости равного давления имеет вид
![]()
Это уравнение называется уравнением поверхности жидкости равного или постоянного давления. Рассмотрим наиболее часто встречающиеся случаи.
Первый
случай,когда
на покоящуюся жидкость действует одна
внешняя сила, сила тяжести,
тогда ![]() ,
, ![]() ,
, ![]() (направление
ускорения свободного падения не совпадает
с положительным направлением оси Z). В
этом случае исходное уравнение имеет
вид
(направление
ускорения свободного падения не совпадает
с положительным направлением оси Z). В
этом случае исходное уравнение имеет
вид
![]() или
или ![]()
т. е. получаем поверхности равного давления, представляющие собой семейство горизонтальных плоскостей. Каждому значению Zсоответствует плоскость, точки которой имеют определенное постоянное значение давления. Свободная поверхность жидкости (для ограниченного объема), в данном случае—одна из плоскостей равного давления. Имеем в виду, что свободная поверхность — это поверхность на границе жидкой и газообразной сред. На свободную поверхность будет приложено постоянное давление равное атмосферному.
Сначала рассмотрим простейший случай покоя. Жидкость находится под действием силы тяжести. Это означает, что проекции ускорений на оси X и Y отсутствуют. Единственным ускорением является ускорение свободного падения g, т. е.:
![]() ,
, ![]() ,
, ![]() .
.
Тогда полный дифференциал давления после подстановки в него ускорений примет вид:
![]() .
.
После интегрирования этого выражения получим:
![]() .
.
Постоянную интегрирования, равную
![]() ,
,
найдём,
подставив параметры свободной
поверхности ![]() и
и ![]() .
.
После подстановки этих значений в интеграл P будем иметь равенство:
![]()
Переписав это выражение в другом виде, получим

Если обозначить (Z0 - Z) через h, то приведённое равенство примет уже знакомый вид основного уравнения гидростатики
![]() .
.
Из этого же равенства можно получить следующий вид
![]() ,
,
или

Последнее выражение часто называют основным законом гидростатики.
Вопрос №13. Виды движения жидкости. Измерение расхода жидкости, приборы
Проведём классификацию видов движения жидкости.
1. Классификация по признаку зависимости движения жидкости от времени.
1.1. Установившееся (стационарное).
1.2. Неустановившееся (нестационарное).
2. Классификация по признаку учёта сил трения, вязкости и теплопроводности.
2.1. Идеальная невязкая жидкость.
2.2. Вязкая жидкость.
3. Классификация по виду движения жидкости (поступательное или вращательного движение).
3.1. Безвихревое (потенциальное) (движение, когда вращение отсутствует).
3.2. Вихревое движение.
4. Классификация по характеру изменения плотности в потоке.
4.1. Несжимаемая (жидкость), r=const.
4.2. Сжимаемая (газ), r¹const.
5. Классификация по скорости и её отношению к скорости
расширяющихся
возмущений (скорости звука).

5.1. Дозвуковое ( M<1) , где , V - скорость потока, а – скорость звука.
![]() 5.2.
Трансзвуковое (М»1).
5.2.
Трансзвуковое (М»1).
5.3. Сверхзвуковое (М>1).
5.4. Гиперзвуковое (М>>1).
6. Классификация по режиму течения.
6.1. Ламинарный режим, (Re£Reкр).
6.2. Турбулентный режим,(Re/Reкр).
7. Вид течения.
7.1. Свободное.
7.2. Вынужденное.
Вопрос №14 Струйная модель движения жидкости, параметры потока.
В гидравлике рассматривается струйная модель движения жидкости, т.е. поток представляется как совокупность элементарных струек жидкости, имеющих различные скорости течения us. Индекс S означает (напоминает), что в каждой точке живого сечения скорости различны. Элементарные струйки как бы скользят друг по другу. Они трутся между собой и вследствие этого их скорости различаются. Причём, в середине потока скорости наибольшие, а к периферии они уменьшаются. Распределение скоростей по живому сечению потока можно представить в виде параболоида с основанием, равным S. Высота его в любой точке равна скорости соответствующей элементарной струйки uS. Площадь элементарной струйки равна dS. В пределах этой площади скорость можно считать постоянной. Понятно, что за единицу времени через живое сечение потока будет проходить объём жидкости Vt, равный объёму параболоида. Этот объём жидкости и будет равен расходу потока.
![]() .
.
С учётом понятия средней скорости, которая во всех точках живого сечения одинакова, за единицу времени через живое сечение потока будет проходить объём жидкости (обозначим его Vtср ), равный:
Vtср=SVср.
Если приравнять эти объёмы Vtср = Vt=параболоида, можно определить значение средней скорости потока жидкости:

В дальнейшем среднюю скорость потока жидкости будем обозначать буквой V без индекса ср.
При неравномерном движении средняя скорость в различных живых сечениях по длине потока различна. При равномерном движении средняя скорость по длине потока постоянна во всех живых сечениях.
Вопрос №15. Уравнение неразрывности потока.
Рассмотрим установившийся поток между живыми сечениями 1,2 ( рис. 26 ).
|
|
Живым сечением называется поверхность в пределах потока, проведенная параллельно к направлению струек. За единицу времени через живое сечение 1 в рассматриваемый объем жидкости
|
где ![]() -
площадь живого сечения,
-
площадь живого сечения,![]() -
средняя скорость в сечении.
-
средняя скорость в сечении.
Через живое сечение 2 за это время вытекает объем жидкости
![]() ,
,
где ![]() -
площадь живого сечения 2,
-
площадь живого сечения 2,![]() -
средняя скорость в сечении 2.
-
средняя скорость в сечении 2.
Поскольку
форма объема 1-2 с течением времени не
изменяется, жидкость несжимаемая, объем
жидкости ![]() должен
равняться объему вытекающему
должен
равняться объему вытекающему![]() .
.
Поэтому можно записать
![]() .
.
Это уравнение называется уравнением неразрывности.
Из уравнения неразрывности следует, что
 .
.
Средние скорости обратно пропорциональны площадям соответствующих сечений.
Вывод основных гидродинамических уравнений начнём с вывода уравнения неразрывности, выражающего закон сохранения в гидродинамике.
Математическое
описание состояния движущейся жидкости
осуществляется с помощью функций,
определяющих распределение скоростей ![]() и
каких-либо двух термодинамических
величин, например,
и
каких-либо двух термодинамических
величин, например,![]() -
давления и
-
давления и![]() -
плотности.
-
плотности.
Скорость, давление и плотность жидкости будем относить к данным точкам пространства, а не к определённым частицам жидкости, передвигающимся во времени и в пространстве. То есть будем пользоваться переменными Эйлера.
|
|
Рассмотрим некоторый объём Vo пространства. Количество (масса) жидкости в этом объёме есть
Через
элемент поверхности
|
Вектор ![]() по
абсолютной величине равен площади
элемента поверхности и направлен по
внешней нормали к ней. Тогда
по
абсолютной величине равен площади
элемента поверхности и направлен по
внешней нормали к ней. Тогда![]() положительно,
если жидкость вытекает из объёма, и
отрицательно, если жидкость втекает в
него.
положительно,
если жидкость вытекает из объёма, и
отрицательно, если жидкость втекает в
него.
Полное количество жидкости, вытекающей в единицу времени из объёма Vo
 .
.
где S - поверхность, ограничивающая выделенный объём Vo.
С другой стороны, уменьшение количества жидкости в объёме Vo можно записать в виде
 .
.
Приравнивая оба выражения, получаем:

 .
.
Интеграл по поверхности преобразуем в интеграл по объёму
 .
.
Таким образом,
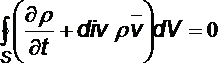 .
.
Поскольку это равенство должно иметь место для любого выделенного объёма, то должно быть равным нулю подынтегральное выражение, т.е.
 .
.
Получили уравнение неразрывности.
Расписав
выражение ![]() можно
записать
можно
записать

![]()
В декартовых координатах
 .
.
Вектор ![]() называют
плотностью потока жидкости.
называют
плотностью потока жидкости.
Его направление совпадает с направлением движения жидкости, а абсолютная величина определяет количество жидкости, протекающей в единице времени через единицу площади, расположенной перпендикулярно к скорости.
Вопрос №16. Дифференцированное уравнение движения идеальной жидкости (Эйлера).
Жидкость, в которой отсутствуют силы сопротивления, называется идеальной.
Уравнения движения идеальной жидкости в проекциях на координатные оси- уравнения Л.Эйлера движения невязкой несжимаемой жидкости

Здесь X, Y, Z — по определению, проекции ускорения массовых сил. При установившемся характере движения идеальной жидкости уравнения Эйлера могут быть проинтегрированы и приведены к виду:
![]()
или
![]()
где Ф - потенциальная функция, такая, что

После интегрирования дифференциального уравнения при постоянстве плотности получаем
![]()
Если массовой силой является сила тяжести, то

Последнее выражение называется полным напором и обычно обозначается Н.
Вопрос № 17. Уравнение Бернулли для идеальной жидкости.
Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач.
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.3.5).

Рис.3.5. Схема к выводу уравнения Бернулли для идеальной жидкости
Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.
Для
измерения давления жидкости
применяют пьезометры -
тонкостенные стеклянные трубки, в
которых жидкость поднимается на высоту ![]() .
В каждом сечении установлены пьезометры,
в которых уровень жидкости поднимается
на разные высоты.
.
В каждом сечении установлены пьезометры,
в которых уровень жидкости поднимается
на разные высоты.
Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.
Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.3.5).
Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.
Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.
Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:
![]()
Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:
![]()
и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.
С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:
z1
и z2 - удельные энергии положения,
характеризующие потенциальную энергию
в сечениях 1-1 и 2-2;
![]() -
удельные энергии давления, характеризующие
потенциальную энергию давления в тех
же сечениях;
-
удельные энергии давления, характеризующие
потенциальную энергию давления в тех
же сечениях;![]() -
удельные кинетические энергии в тех же
сечениях.
-
удельные кинетические энергии в тех же
сечениях.
Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.
Уравнение
Бернулли можно истолковать и чисто
геометрически. Дело в том, что каждый
член уравнения имеет линейную размерность.
Глядя на рис.3.5, можно заметить, что z1 и
z2 - геометрические высоты сечений 1-1 и 2-2 над
плоскостью сравнения; ![]() -
пьезометрические высоты;
-
пьезометрические высоты;![]() -
скоростные высоты в указанных сечениях.
-
скоростные высоты в указанных сечениях.
В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.
Вопрос №18 Геометрическая и энергетическая интерпритация уравнения Д. Бернулли.
Положение любой частицы жидкости относительно некоторой произвольной линии нулевого уровня 0-0 определяется вертикальной координатой Z. Для реальных гидравлических систем это может быть уровень, ниже которого жидкость из данной гидросистемы вытечь не может. Например, уровень пола цеха для станка или уровень подвала дома для домашнего водопровода.
Как и в гидростатике, величину Z называют нивелирной высотой.
![]()
Второе слагаемое - носит название пьезометрическая высота. Эта величина соответствует высоте, на которую поднимется жидкость в пьезометре, если его установить в рассматриваемом сечении, под действием давления P.

Сумма первых двух членов уравнения ѕ гидростатический напор.
![]()
Третье слагаемое в уравнения Бернулли называется скоростной высотой или скоростным напором. Данную величину можно представить как высоту, на которую поднимется жидкость, начавшая двигаться вертикально со скорость u при отсутствии сопротивления движению.
Сумму всех трёх членов (высот) называют гидродинамическим или полным напором и, как уже было сказано, обозначают буквой Н.
|
| |
|
|
|
Все слагаемые уравнения Бернулли имеют размерность длины и их можно изобразить графически.
Значения  -нивелирную,
пьезометрическую и скоростную высоты можно
определить для каждого сечения
элементарной струйки жидкости.
Геометрическое место точек, высоты
которых равны
-нивелирную,
пьезометрическую и скоростную высоты можно
определить для каждого сечения
элементарной струйки жидкости.
Геометрическое место точек, высоты
которых равны  ,
называетсяпьезометрической
линией.
Если к этим высотам добавить скоростные
высоты, равные
,
называетсяпьезометрической
линией.
Если к этим высотам добавить скоростные
высоты, равные ![]() ,
то получится другая линия, которая
называетсягидродинамической или напорной
линией.
,
то получится другая линия, которая
называетсягидродинамической или напорной
линией.
Из уравнения Бернулли для струйки невязкой жидкости (и графика) следует, что гидродинамический напор по длине струйки постоянен.
Выше
было получено уравнение Бернулли с
использованием 
энергетических характеристик жидкости. Суммарной энергетической характеристикой жидкости является её гидродинамический напор.
С физической точки зрения это отношение величины механической энергии к величине веса жидкости, которая этой энергией обладает. Таким образом, гидродинамический напор нужно понимать как энергию единицы веса жидкости. И для идеальной жидкости эта величина постоянна по длине. Таким образом, физический смысл уравнения Бернулли это закон сохранения энергии для движущейся жидкости.

Здесь с энергетической точки зрения (в единицах энергии, Дж/кг) gz — удельная потенциальная энергия положения; Р/r — удельная потенциальная энергия давления; gz + Р/r — удельная потенциальная энергия; u2/2 — удельная кинетическая энергия; и — скорость элементарной струйки идеальной жидкости.
Умножив все члены уравнения на удельный вес жидкости g, получим
![]()
gz - весовое давление, Па; P — гидродинамическое давление, Па; rи2 /2 — динамическое давление Па; gH — полное давление, Па
Вопрос №19. Два режима движения жидкости. Число Рейнольдса.
В 1883 году английским учёным Осборном Рейнольдсом (1842-1912 гг.) было установлено, что критерием режима течения жидкости является безразмерная величина, представляющая собой отношение произведения средней скорости потока и линейного размера, характерного для живого сечения, к кинематической вязкости жидкости n.

Критерий режима течения жидкости называется числом Рейнольдса.
При течении жидкости в круглых трубах за характерный размер l объёма принимается внутренний диаметр трубы D, тогда
 .
.
Пример. Установить,
какой режим будет в трубе диаметра D=20
см, если средняя скорость ![]() ,
а кинематическая вязкость
,
а кинематическая вязкость .
.
Розв`язування.  =
60000 > 1000 - режим турбулентний.
=
60000 > 1000 - режим турбулентний.
Опытные данные Рейнольдса показывают наличие трёх областей:
АК - ламинарной, ВК - переходной или неустойчивый, ВС - турбулентной ( рис. 41 ).

Рис. 41
Точки К и В называются критическими точками, точками, в которых происходит смена режима течения.
Ниже точки К режим всегда ламинарный, выше точки В - турбулентный.
В зависимости от изменения скорости от малых значений к большим и от больших к малым ламинарный режим удерживается до точки В при увеличении скорости, или при уменьшении до точки К.
Значение числа Рейнольдса, соответствующее нижней критической точке К, называется нижним критическим числом Рейнольдса, число Re соответствует верхней критической точке - верхним критическим числом Рейнольдса.
Нижнее число Рейнольдса Re= 956.
Переход к турбулентному режиму зависит (помимо скорости течения, вязкости и характерного размера) от ряда факторов - источников питания трубопровода, шероховатости труб, местных сопротивлений и т.д. Верхнее число Рейнольдса обычно принимают равным Re= 5000.
На практике ламинарный режим встречается
1) при движении очень вязких жидкостей,
2) при движении жидкости в тонких ( капилярных ) трубах,
3) при движении воды в грунтах.
Турбулентный режим наблюдается значительно чаще: при движении в каналах, трубах и т.д.
Профиль скорости при ламинарном и турбулентном режиме течения
При ламинарном режиме жидкости движение как бы разделяется на бесконечно большое число тонких коаксиально расположенных относительно оси трубопровода слоёв.
Распределение скоростей по сечению имеет вид параболы. Скорость у стены равна нулю. При удалении от стенки скорости возрастают и достигают максимума на оси трубы.

а б
Рис. 42
Определим закон распределения скорости. Выделим объём жидкости в виде цилиндра радиуса r и длиной l и составим уравнение равновесия ( рис. 42 )
 .
.
Движение установившееся, скорости на одном радиусе одинаковы.
 .
.
С учётом гидравлического уклона
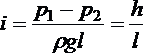 ,
,
имеем
 .
.
Проинтегрируем по сечению трубы, учитывая, что при r=r0 и u=0, получим закон распределения скоростей в сечении
 .
.
Максимум скорости при r=0
 .
.
Определим расход жидкости через трубу
 .
.
Средняя скорость
 .
.
Соотношение между максимальной и средней скоростью
 .
.
Турбулентный режим движения жидкости характеризуется беспорядочным движением частиц. При этом режиме частицы жидкости движутся по произвольным траекториям и с различной скоростью. Скорость изменяется по величине и направлению около среднего значения.
Такое изменение скорости называется пульсацией скорости. Среднюю по времени скорость называют осреднённой скоростью. Связь между осреднённой и мгновенной скоростью может быть выражена зависимостью
 ,
,
где Т - период наблюдения.
Распределение скоростей течения в этом случае выглядит иначе, чем при ламинарном режиме( рис. 43 ).
|
Рис. 43 1-ламинарная плёнка, 2-переходный слой, 3-ядро турбулентного потока |
В ламинарной пленке и переходном слое скорости течения изменяются так же, как при ламинарном режиме течения. В переходной зоне зарождаются вихри, обусловленные увеличением скорости движения, влиянием выступов шероховатости.
|
Если выступы шероховатости меньше толщины ламинарной пленки, стенка будет гидравлически гладкой. При величине выступов выше толщины ламинарной пленки, неровности стенок будут увеличивать беспорядочность движения и стенка будет гидравлически шероховатой.
Возникающие в пограничном слое вихри проникают в центральную часть потока и образуют ядро турбулентного течения. В ядре потока происходит интенсивное и непрерывное перемешивание частиц жидкости.
Для описания профиля скорости в ядре течения турбулентного состояния используется логарифмический закон распределения скоростей
 .
.
Величина коэффициента трения зависит от режима течения жидкости.
Опытами было установлено, что при течении жидкости возможны два режима: ламинарный и турбулентный.
|
Рис. 39 |
При ламинарном режиме жидкость течёт слоями, не перемешиваясь ( рис. 39 ).
|
|
Рис. 40 |
При турбулентном частицы жидкости интенсивно перемешиваются ( рис. 40 ).
|
Ламинарное и турбулентное течение жидкости можно наблюдать в стеклянной трубе В ( рис. 39, 40 ).
Питание трубы производится из бака, а скорость течения регулируется краном С. Для наблюдения за характером движения жидкости по тонкой трубке в трубу В подводится подкрашенная жидкость такой же плотности, как и движущаяся жидкость (например, чернило).
При малых скоростях в трубе В струйка продолжает двигаться, не перемешиваясь с остальной жидкостью, что указывает на ламинарный режим течения.
При больших скоростях в трубе струйка очень сильно перемешивается со всей жидкостью, что указывает на турбулентный режим.
Вопрос №20. Основное уравнение равномерного движения жидкости. Формула Шези.
Рассмотрим прямолинейное равномерное движение жидкости. Живые сечения в этом случае могут быть произвольной формы, но не должны изменяться по всей длине рассматриваемого участка. В таком потоке потери напора определяются лишь потерями по длине.
Выделим из потока участок жидкости длиной l и запишем уравнение Бернулли для сечений 1 и 2( рис. 32 )

Рис. 38

где
z1 , z2 - ординаты центра тяжести сечений 1,2,
p1 , p2 - давление в центрах тяжести этих сечений,
v1 , v2 - средние скорости в этих сечениях,
h1-2 - потери напора по длине.
Так как движение равномерное, то v1 =v2 и уравнение можно переписать так:
 .
(1)
.
(1)
В случае равномерного движения разность удельных потенциальных энергий равна потере напора по длине.
Для вычисления этой разности напишем сумму проекций на ось А-А всех сил, действующих на участке 1-2. Эти силы следующие:
1) сила тяжести жидкости
![]() ,
,
2) силы давления на плоские сечения
![]() ,
, ![]() ,
, ![]() ,
,
3) сила трения
![]() ,
,
где t - сила трения на единицу площади смачиваемой поверхности
русла, c - смоченный периметр,
4) силы давления стенок на жидкость ( эти силы не подсчитываем, так как они параллельны оси А-Аи, следовательно, их проекции на ось А-А равны нулю ).
Спроектируем все эти силы на ось А-А:
![]() .
.
Из рисунка
 .
.
Подставим выражение для сил в уравнение
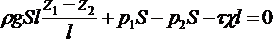 .
.
Разделим
обе части этого равенства на ![]() ,
имеем
,
имеем
 .
(2)
.
(2)
Сравнивая выражения (1) и (2), находим
 ,
,
откуда
 .
.
Отношение площади живого сечения S к смоченному периметру c называется гидравлическим радиусом
 .
.
Величина ![]() обозначается
через i и
называется гидравлическим
уклоном.
обозначается
через i и
называется гидравлическим
уклоном.
Получаем
 .
.
Это уравнение называется основным уравнением равномерного движения.
Величина ![]() имеет
размерность квадрата скорости
имеет
размерность квадрата скорости
 .
.
Выражение![]() -
называется динамической
скоростью,
обозначается v*
-
называется динамической
скоростью,
обозначается v*
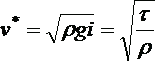 .
.
Формула Шези — формула для определения средней скорости потока при установившемся равномерном турбулентном движении жидкости в области квадратичного сопротивления для случая безнапорного потока. Опубликована французским инженером-гидравликом А. Шези (Antoine de Chézy, 1718–1798) в 1769 году. Применяется для расчётов потоков в речных руслах и канализационых системах.
![]() ,
,
где V — средняя скорость потока, м/с;
C — коэффициент сопротивления трения по длине (коэффициент Шези), являющийся интегральной характеристикой сил сопротивления;
R — гидравлический радиус, м;
I — гидравлический уклон м/м.
Формула
Шези имеет то же предназначение, что
и формула
Дарси-Вейсбаха.
Коэффициент потерь на трение ![]() связан
с коэффициентом сопротивленияС
следующей
зависимостью:
связан
с коэффициентом сопротивленияС
следующей
зависимостью:
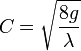 .
.
Коэффициент сопротивления C может быть определён по формуле Н. Н. Павловского:
![]()
где n — коэффициент шероховатости, характеризующий состояние поверхности русла, для случая канализационных труб принимается в диапазоне (0,012...0,015); для других случаев nbsp;— информация приведена в литературе[1]
у — показатель степени, зависящий от величины коэффициента шероховатости и гидравлического радиуса:
![]()
Эта формула рекомендуется для значений R < (3...5)м. При больших гидравлических радиусах или других значениях коэффициентов шероховатости применение формулы Н. Н. Павловского в гидравлических расчётах речных русел приводит к значительным ошибкам.
При значении y = 1/6 формула Шези приводится к формуле Маннинга.
Существуют и другие эмпирические формулы для определения коэффициента сопротивления C[2]
Вопрос №21. Гидравлические сопротивления. Формулы Дарси-Вейсбаха.
Гидравлическая жидкость в гидросистемах технологического оборудования, как уже обсуждалось ранее, играет роль рабочего тела. Она обеспечивает перенос энергии от источника гидравлической энергии к потребителю (в большинстве случаев, к гидродвигателю). Для такого переноса используются напорные потоки. В подобных потоках жидкость со всех сторон ограничена твёрдыми стенками трубопроводов, каналов гидроаппаратов и полостей гидромашин. В дальнейшем мы будем ориентироваться именно на такие случаи, хотя аналогичные процессы сопровождают и движение безнапорных потоков.
Естественно, что твёрдые стенки препятствуют свободному движению жидкости. Поэтому при относительном движении жидкости и твердых поверхностей неизбежно возникают (развиваются) гидравлические сопротивления. На преодоление возникающих сопротивлений затрачивается часть энергии потока. Эту потерянную энергию называют гидравлическими потерями удельной энергии или потерями напора. Гидравлические потери главным образом связаны с преодолением сил трения в потоке и о твёрдые стенки и зависят от ряда факторов, основными из которых являются:
геометрическая форма потока,
размеры потока,
шероховатость твёрдых стенок потока,
скорость течения жидкости,
режим движения жидкости (который связан со скоростью, но учитывает её не только количественно, но и качественно),
вязкость жидкости,
некоторые другие эксплуатационные свойства жидкости.
Но гидравлические потери практически не зависят от давления в жидкости.
Величина
гидравлических потерь оценивается
энергией, потерянной каждой весовой
единицей жидкости. Из уравнения Бернулли,
составленного для двух сечений потока,
обозначенных индексами 1 и 2 потери
энергии потока жидкости ![]() можно
представить как
можно
представить как![]()
Потери напора по длине, иначе их называют потерями напора на трение, в чистом виде, т.е. так, что нет никаких других потерь, возникают в гладких прямых трубах с постоянным сечением при равномерном течении. Такие потери обусловлены внутренним трением в жидкости и поэтому происходят и в шероховатых трубах, и в гладких. Величина этих потерь выражается зависимостью
 ,
,
где ![]() -
коэффициент сопротивления, обусловленный
трением по длине.
-
коэффициент сопротивления, обусловленный
трением по длине.
При равномерном движении жидкости на участке трубопровода постоянного диаметра d длиной l этот коэффициент сопротивления прямо пропорционален длине и обратно пропорционален диаметру трубы
![]() ,
,
где l– коэффициент гидравлического трения (иначе его называют коэффициент потерь на трение или коэффициент сопротивления трения).
Из этого выражения нетрудно видеть, что значение l - коэффициент трения участка круглой трубы, длина которого равна её диаметру.
С учетом последнего выражения для коэффициента сопротивления потери напора по длине выражаются формулой Дарси
 .
.
Эту
формулу можно применять не только для
цилиндрических трубопроводов, но тогда
надо выразить диаметр
трубопровода d через гидравлический
радиус потока ![]()
![]() или
или ![]()
где, напомним, Й – площадь живого сечения потока,
З - смоченный периметр.
Гидравлический радиус можно вычислить для потока с любой формой сечения, и тогда формула Дарси принимает вид
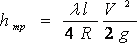 .
.
Эта формула справедлива как для ламинарного, так и для турбулентного режимов движения жидкости, однако коэффициент трения по длине »не является величиной постоянной.
Для
определения физического смысла
коэффициента »рассмотрим
объём жидкости длиной l,
который равномерно движется в трубе
диаметром d со
скоростьюV.
На этот объём действуют силы
давления P1 и P2,
причём P1> P2,
и силы трения рассматриваемого объёма
о стенки трубы, которые определяются
напряжением трения на стенке трубы Д0.
Условием равномерного движения под
действием сказанных сил будет следующее
равенство: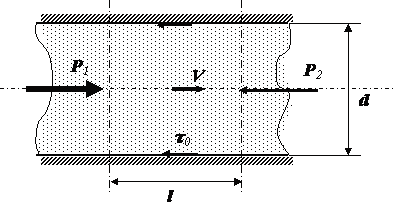
![]() .
.
Если учесть, что
 , то
, то  ,
,
и подставить эту величину в уравнение сил, действующих на рассматриваемый объём, получим:
 .
.
Сократив
последнее выражение, получим  .
Выразив из него »,
окончательно будем иметь
.
Выразив из него »,
окончательно будем иметь
 .
.
Местными
гидравлическими сопротивлениями называются
любые участки гидравлической системы,
где имеются повороты, преграды на пути
потока рабочей жидкости, расширения
или сужения, вызывающие внезапное
изменение формы потока, скорости или
направления ее движения. В этих местах
интенсивно теряется напор. Примерами
местных сопротивлений могут быть
искривления оси трубопровода, изменения
проходных сечений любых гидравлических
аппаратов, стыки трубопроводов и т.п.
Потери напора на местных
сопротивлениях ![]() определяются
по формуле
Вейсбаха:
определяются
по формуле
Вейсбаха:
 ;
;
где ![]() -
коэффициент местного сопротивления.
-
коэффициент местного сопротивления.
Коэффициент местного сопротивления зависит от конкретных геометрических размеров местного сопротивления и его формы. В связи со сложностью процессов, которые происходят при движении жидкости через местные сопротивления, в большинстве случаев его приходится определять на основании экспериментальных данных.
Однако в некоторых случаях величины коэффициентов местных сопротивлений можно определить аналитически.
Из
определения коэффициента ![]() видно,
что он учитывает все виды потерь энергии
потока жидкости на участке местного
сопротивления. Его физический смысл
состоит в том, что он показывает долю
скоростного напора, затрачиваемого на
преодоление данного сопротивления.
видно,
что он учитывает все виды потерь энергии
потока жидкости на участке местного
сопротивления. Его физический смысл
состоит в том, что он показывает долю
скоростного напора, затрачиваемого на
преодоление данного сопротивления.
Коэффициенты
различных сопротивлений можно найти в
гидравлических справочниках. В том
случае, если местные сопротивления
находятся на расстоянии меньше (25ч50)d
друг от друга (![]() -
диаметр трубопровода, соединяющего
местные сопротивления), весьма вероятно
их взаимное влияние друг на друга, а их
действительные коэффициенты местных
сопротивлений будут отличаться от
табличных. Такие сопротивления нужно
рассматривать как единое сложное
сопротивление, коэффициент
-
диаметр трубопровода, соединяющего
местные сопротивления), весьма вероятно
их взаимное влияние друг на друга, а их
действительные коэффициенты местных
сопротивлений будут отличаться от
табличных. Такие сопротивления нужно
рассматривать как единое сложное
сопротивление, коэффициент ![]() которого
определяется только экспериментально.
Нужно отметить, что из-за взаимного
влияния местных сопротивлений,
расположенных вблизи друг друга в
потоке, во многих случаях суммарная
потеря напора не равна простой сумме
потерь напора на каждом из этих
сопротивлений.
которого
определяется только экспериментально.
Нужно отметить, что из-за взаимного
влияния местных сопротивлений,
расположенных вблизи друг друга в
потоке, во многих случаях суммарная
потеря напора не равна простой сумме
потерь напора на каждом из этих
сопротивлений.
Это трубопроводы постоянного по длине диаметра, у которых основными являются потери напора по длине, а местными потерями напора и скоростным напором можно пренебречь.
Потери напора по длине трубопровода определяют по формуле Дарси—Вейсбаха:
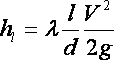
Учитывая,
что расход Q = VЧS и
скорость движения потока ![]() тогда
тогда
 или
или
![]()
где А — удельное
сопротивление трубопровода, определяемое
по справочным таблицам; 
Для переходной области удельное сопротивление Ао=А*b,
где b — поправочный коэффициент, учитывающий зависимость коэффициента гидравлического трения l от числа Рейнольдса.
Кроме удельного сопротивления А в литературе по гидравлике для решения задач приводится способ расчета длинных трубопроводов, базирующийся на формуле Шези.
Широко
применяемые гидравлические параметры
— это модуль расхода ![]() , сопротивление
трубопровода ST=A*l, проводимость
трубопровода
, сопротивление
трубопровода ST=A*l, проводимость
трубопровода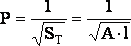 . С
помощью вышеуказанных параметров потери
напора по длине можно определить
следующим образом:
. С
помощью вышеуказанных параметров потери
напора по длине можно определить
следующим образом:

Вопрос №22. Гидравлический коэффициент трения, его зависимость и определение
Как показывают исследования, при ламинарном течении жидкости в круглой трубе максимальная скорость находится на оси трубы. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. От стенок трубы к ее оси скорости нарастаю плавно. График распределения скоростей по поперечному сечению потока представляет собой параболоид вращения, а сечение параболоида осевой плоскостью - квадратичную параболу (рис.4.3).
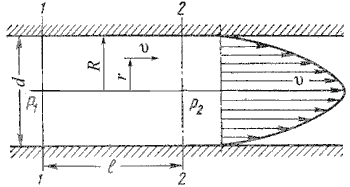
Рис. 4.3. Схема для рассмотрения ламинарного потока
Уравнение, связывающее переменные υ и r, имеет следующий вид:
![]()
где P1 и P2 - давления соответственно в сечениях 1 и 2.
У стенок трубы величина r = R, , значит скорость υ = 0, а при r = 0 (на оси потока) скорость будет максимальной
![]()
Теперь определим расход жидкости при ламинарном течении в круглой трубе. Так как эпюра распределения скоростей в круглой трубе имеет вид параболоида вращения с максимальным значением скорости в центре трубы, то расход жидкости численно равен объему этого параболоида. Определим этот объем.
Максимальная скорость дает высоту параболоида
![]()
Как известно из геометрии, объем параболоида высотой h и площадью ρR2 равен
![]()
а в нашем случае
![]()
Если вместо R подставить диаметр трубы d, то формула (4.4) приобретет вид
![]()
Расход в трубе можно выразить через среднюю скорость:
![]()
откуда
![]()
Для определения потерь напора при ламинарном течении жидкости в круглой трубе рассмотрим участок трубы длиной l, по которому поток течет в условиях ламинарного режима (рис.4.3).
Потеря давления в трубопроводе будет равна
![]()
Если в формуле динамический коэффициент вязкости μ заменить через кинематический коэффициент вязкости υ и плотность ρ ( μ = υ ρ ) и разделить обе части равенства на объемный вес жидкости γ = ρ g, то получим:
![]()
Так как левая часть полученного равенства равна потерям напора hпот в трубе постоянного диаметра, то окончательно это равенство примет вид:
![]()
Уравнение может быть преобразовано в универсальную формулу Вейсбаха-Дарси, которая окончательно записывается так:
![]()
где λ - коэффициент гидравлического трения, который для ламинарного потока вычисляется по выражению:
![]()
Однако при ламинарном режиме для определения коэффициента гидравлического трения λ Т.М. Башта рекомендует при Re < 2300 применять формулу
![]()


 .
. .
. Рис.
17
Рис.
17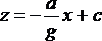
 Рис.
18
Рис.
18 .
. Рис.
19
Рис.
19 .
.
 .
.
 Рис.
24
Рис.
24 Рис.
26
Рис.
26 Рис.
11
Рис.
11 .
.


