
Термех_Кинематика
.pdf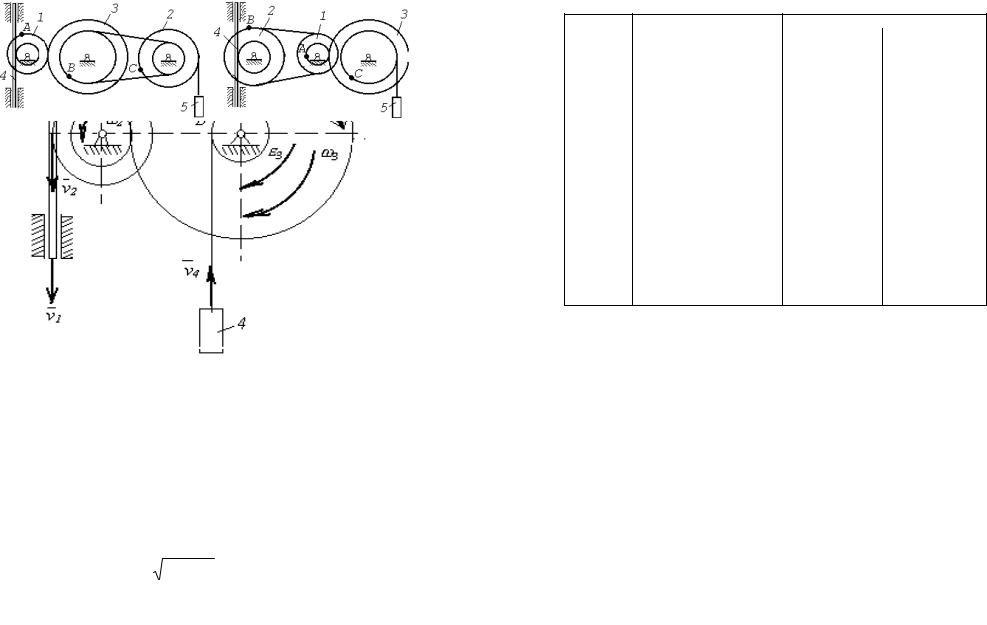
Тогда для момента времени t1 = 3 с получим ω3 = 6,75 с-1.
2. Определим ϑ4 . Так как ϑ4 =ϑB = ω3r3 , то при t1 = 3 c
ϑ4 = 20,25 см/с.
3. Определяем ε3. Учитывая второе из равенств (2) получим ε3 =
ω3 = 1,5t. Тогда при t1 = 3 c ε3 = 4,5 c-2.
4. Определяем aA. Для точки А aA = aAτ + aAn , где численно
a |
Aτ |
= R ε |
3 |
, a |
An |
= R ω2 |
. Тогда для момента времени t1 = 3 с имеем |
|
3 |
|
3 3 |
|
aAτ =36см/с2, aAn =364,5 см/с2;
a = a2τ +a2 =366,3 см/с2.
A a An
Все скорости и ускорения точек, а также направления угловых
скоростей показаны на рис. К2.
Ответ: ω3 = 6,75 с-1, ϑ4 = 20,25 см/с, ε3 = 4,5с-2, aA = 366,3 см/с2 .
Таблица К2
Номер |
Дано |
|
Найти |
|
условия |
Скорости |
Ускорение |
||
|
0 |
s4 = 4(7t −t2 ) |
ϑ |
B |
, ϑ |
C |
ε |
2 |
, a |
A |
, a |
|
|
|
|
|
|
5 |
||||
1 |
ϑ5 = 2(t2 −3) |
ϑA , ϑC |
ε3 , aB , a4 |
|||||||
2 |
ϕ1 = 2t2 −9 |
ϑ |
4 |
,ω |
2 |
ε |
2 |
, a |
C |
, a |
|
|
|
|
|
|
5 |
||||
3 |
ω2 = 7t −3t2 |
ϑ |
5 |
, ω |
3 |
ε2 , aA , a4 |
||||
4 |
ϕ3 =3t −t2 |
ϑ |
, ω |
ε1 , aB , a5 |
||||||
|
|
|
4 |
|
1 |
|
|
|
|
|
5 |
ω1 = 5t −2t2 |
ϑ ,ϑ |
B |
ε2 , aC , a4 |
||||||
|
|
|
5 |
|
|
|
|
|
|
|
6 |
ϕ2 = 2(t2 −3t) |
ϑ |
, ω |
ε1 , aC , a5 |
||||||
|
|
|
4 |
|
1 |
|
|
|
|
|
7 |
ϑ4 =3t2 −8 |
ϑ |
A |
, ω |
ε3 , aB , a5 |
|||||
|
|
|
|
3 |
|
|
|
|
|
|
8 |
s5 = 2t2 −5t |
ϑ4 ,ω2 |
ε1 , aC , a4 |
|||||||
9 |
ω3 =8t −3t2 |
ϑ5 , ωB |
ε2 , aA , a4 |
|||||||
Рис. К2.0 |
Рис. К2.1 |
Рис. К2.2 |
Рис. К2.3 |
101 |
102 |
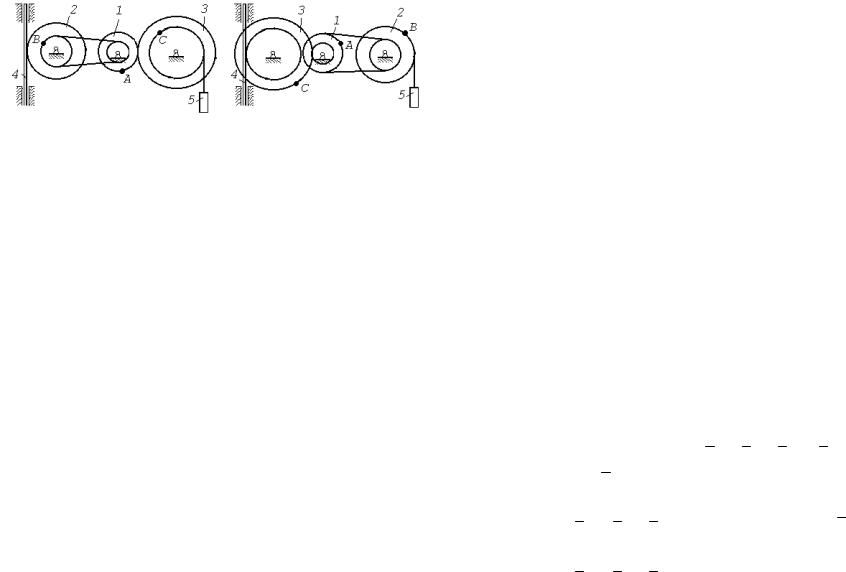
Рис. К2.4 |
Рис. К2.5 |
Рис. К2.6 |
Рис. К2.7 |
Рис. К2.8 |
Рис. К2.9 |
Задача К3
Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна В или Е (рис. К3.0–К3.7) или из стержней 1, 2, 3 и ползунов В и Е (рис. К3.8, К3.9), соединенных друг с другом и с неподвижными опорами О1, О2 шарнирами; точка Д находится в середине стержня
103
АВ. Длины стержней равны соответственно: 1 = 0,4 м, 2 = 1,2 м,
3 = 1,4 м, 4 = 0,6 м.
Положение механизма определяется углами α, β, γ, ϕ, θ. Значения этих углов и других заданных величин указаны в табл. К3а (для рис. 0–4) или в табл. К3б (для рис. 5–9); при этом в табл. К3а ω1 и ω4 –– величины постоянные.
Определитьвеличины, указанные в таблицах встолбцах «Найти». Дуговые стрелки на рисунках показывают, как при построении чертежа механизма должны откладываться соответствующие углы: по ходу или против хода часовой стрелки (например, угол γ на рис. 8 следует отложить от ДВ по ходу часовой стрелки, а на рис. 9 ––
против часовой стрелки и т.д.).
Построение чертежа начинать со стержня, направление которого определяется углом α; ползун с направляющими для большей наглядности изобразить так, как в примере К3 (рис. К3, б).
Заданные угловую скорость и угловое ускорение считать направленными против хода часовой стрелки, а заданные скорости vB и ускорение аB –– от точки В к b (на рис. 5–9).
Указания. Задача К3 –– на исследование плоскопараллельного движения твердого тела. При ее решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности.
При определении ускорений точек механизма исходить из век-
торного равенства а aB = a©A +aτBA +anBA , где А –– точка, ускоре-
ние a A которой или задано, или непосредственно определяется по условиям задачи (если точка А движется по дуге окружности, то
a A = aτA + a nA ); В –– точка, ускорение a B которой нужно определить (если точка В движется по дуге окружности радиуса , то
a B = aτB + anB , где численно aBn = vB2 / . Входящая сюда скорость vB определяется так же, как и скорости других точек меха-
низма, –– длина звена).
104

Пример К3. Механизм (рис. К3, а) состоит из стержней 1, 2, 3, 4 и ползуна В, соединенных друг с другом и с неподвижными опорами О1 и О2 шарнирами.
Дано: α = 60°, β = 150°, γ = 90°, ϕ = 30°, θ = 30°,
АД = ДВ, 1 = 0,4 м, |
2 = 1,2 м, 3 = 1,4 м, ω1 = 2 c-1, ε1 = 7 с-2 |
(направления ω1 и ε1 –– против хода часовой стрелки). |
|
Определить: vB, vE, |
ω2, aB, ε3. |
Рис. К3, а
Рис. K3, б
Решение. 1. Строим положение механизма в соответствии с заданными углами (рис. К3, б).
2. Определяем VB. Точка В принадлежит стержню АВ. Чтобы найти VB, надо знать скорость какой-нибудь другой точки этого
стержня и направление V B . По данным задачи, учитывая направление ω1, можем определить V A численно:
VA = ω1 1 = 0,8 м/с; |
V |
A O1 A. |
(1) |
Направление V B найдем, учтя, что точка В принадлежит одновременно ползуну, движущемуся вдоль направляющих поступа-
тельно. Теперь, зная V A и направление V B , воспользуемся теоре-
мой о проекциях скоростей двух точек тела (стержня АВ) на прямую, соединяющую эти точки (прямая АВ).
Сначала по этой теореме устанавливаем, в какую сторону на-
правлен вектор V B (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим:
VB cos30 =VA cos60 и VB =0,46 м/с. (2)
3. Определяем VЕ. Точка Е принадлежит стержню ДЕ. Следовательно, по аналогии с предыдущим, чтобы определить VЕ, надо сначала найти скорость точки Д, принадлежащей одновременно стержню АВ. Для
этого, зная V А и V B , строим мгновенный вектор скоростей (МЦС) стержня АВ; эта точка С3, лежащая на пересечении перпендикуляров к
V А и V B , восстановленных из точек А и В (к V А перпендикулярен
стержень 1). По направлению вектора V А определяем направление по-
ворота стержня АВ вокруг МЦС С3. Вектор V D перпендикулярен от-
резку С3D, соединяющему точки D и С3, и направлен в сторону поворота. ВеличинуVD найдемизпропорции
VD |
= |
VB |
|
|
|
|
. |
(3) |
|
C D |
C B |
|||
3 |
|
3 |
|
|
105 |
106 |

Чтобы вычислить С3D и С3B, заметим, что ΑC3B –– прямоугольный, таккакострыеуглывнемравны30° и60°, и чтоС3B = АВsin 30° = 0,5 АВ = ВД. Тогда BC3D являетсяравносторонним иС3B = С3D.
В результате равенство (3) дает
VD =VB = 0,46 м/с; |
V |
D C3 D. |
(4) |
Так как точка Е принадлежит одновременно стержню С2Е, вращающемуся вокруг О2, то V E O2 E . Тогда, восставляя из точек Е
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и D перпендикуляры к скоростям |
V E |
и V D , построим |
МЦС С2 |
|||||||||||||||
стержня ДЕ. |
По направлению вектора |
V |
D определяем направле- |
|||||||||||||||
ние поворота стержня ДЕ вокруг центра С2. |
|
|||||||||||||||||
Вектор |
V |
E |
направлен в сторону поворота этого стержня. Из |
|||||||||||||||
рис. К3, б видно, что C2 ED = C2 DE = 30 , откуда С2Е = С2D. |
||||||||||||||||||
Составив теперь пропорцию, найдем, что |
|
|||||||||||||||||
|
|
|
|
VE |
= |
|
VD |
|
, VE =VD = 0,46 м/с. |
(5) |
||||||||
|
|
|
|
|
C2 D |
|||||||||||||
|
|
|
|
C2 E |
|
|
|
|
|
|
|
|
|
|||||
4. Определим ω2. Так как МЦС стержня 2 известен (точка С2) и |
||||||||||||||||||
|
|
|
|
C D = |
|
|
2 |
|
= 0,69, |
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||
то |
2 |
|
|
2cos30 |
|
|
|
|
|
(6) |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
ω2 = |
VD |
= 0,67 c−1. |
|
|||||||||||
|
|
|
|
C2D |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. Определяем a B . Точка В принадлежит стержню АВ. Чтобы
найти a B , надо знать ускорение какой-нибудь другой точки стержня АВ и траекторию точки В. По данным задачи можем определить
a A = aτA + anA , где численно
aAτ |
= ε1 |
1 = 2,8 |
м/с2 ; |
(7) |
|
an |
= ω2 |
|
=1,6 |
м/с2 . |
|
1 |
|
||||
A |
1 |
|
|
|
|
Вектор a nA направлен вдоль АО1, а a τA –– перпендикулярно;
АО1. Изображаем эти векторы на чертеже.
Так как точка В одновременно принадлежит ползуну, то вектор
a B параллелен направляющим ползуна. Изображаем вектор аВ на
чертеже, полагая, что он направлен в ту же сторону, что и V B .
Для определения a B воспользуемся векторным равенством
|
B = |
|
τA + |
|
nA + |
|
τBA + |
|
nBA . |
|
a |
a |
a |
a |
a |
(8) |
Изображаем на чертеже векторы a nВA (вдоль АВ от В к А) и
τ
a ВA (в любую сторону перпендикулярно ВА); численно aBAn = ω32 3 . Найдя ω3 c помощью построенного МЦС С3 стержня 3, получим
|
V |
A |
|
V |
A |
− |
|
|
|
ω3 = |
|
= |
|
= 0,66 c 1 и aBAn |
= 0,61 м/с2 . |
(9) |
|||
C3 A |
3 cos30 |
||||||||
|
|
|
|
|
|||||
Таким образом, у величин, входящих в равенство (8), неизвест-
ны только числовые значения аВ и a τB A ; их можно найти, спро-
ектировав обе части равенства (8) на какие-нибудь две оси.
Чтобы определить аВ, спроектируем обе части равенства (8) на направление АВ (ось Х), перпендикулярное неизвестному вектору
a τВ A . Тогда получим
aB cos30 = aAτ cos60 −aAn cos30 +aBAn . |
(10) |
Подставив в равенство (10) числовые значения всех величин из
(7) и (9), найдем, что
аВ = 0,72 м/с2. |
(11) |
107 |
108 |

Так как получилось аВ > 0, то, следовательно, вектор a B направлен так, как показано на рис. К3, б.
6. Определяем ε3. Чтобы найти ε3, сначала определим a τB A .
Для этого обе части равенства (8) спроектируем на направление, перпендикулярное АВ (ось Y). Тогда получим
aB sin 30 = aτA sin 60 +aAn sin 30 +aBAτ . |
(12) |
Подставив в равенство (12) числовые значения всех величин из
(11) и (7), найдем, что a τBA = –3,58 м/с2. Знак указывает, что на-
правление aτВA противоположно показанному на рис. К3, б.
Теперь из равенства |
aBAn = ω32 |
3 получим |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
aτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
ε3 = |
|
BA |
|
|
= 2,56 c−2. |
|
|
|
|
||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: VВ = 0,46 м/с; |
VЕ = 0,46 м/с; ω2 = 0,67 c; аВ = 0,72 м/с2; |
||||||||||||||||||
ε3 = 2,56 с-2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица К3а (к рис. К3.0–К3.4) |
|||||
Но- |
|
|
Углы, градусы |
|
|
|
|
Дано |
|
|
|
Найти |
|
||||||
мер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ус- |
|
|
|
|
|
|
|
|
|
|
|
ω1 |
ω4 |
|
V |
ω |
|
a |
ε |
ло- |
|
|
|
|
|
|
|
|
|
|
|
’ |
’ |
|
|
|
|
|
|
вия |
α |
|
β |
γ |
|
ϕ |
|
|
θ |
1/c |
1/c |
|
то- |
зве |
|
точ- |
зве- |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чек |
-на |
|
ки |
на |
0 |
0 |
|
60 |
30 |
|
0 |
|
120 |
|
|
6 |
- |
|
B,E |
DE |
|
B |
AB |
|
1 |
90 |
|
120 |
150 |
|
0 |
|
30 |
|
|
- |
4 |
|
A,E |
AB |
A |
AB |
||
2 |
30 |
|
60 |
30 |
|
0 |
|
120 |
|
|
5 |
- |
|
B,E |
AB |
B |
AB |
||
3 |
60 |
|
150 |
150 |
|
90 |
|
30 |
|
|
- |
5 |
|
A,E |
DE |
|
A |
AB |
|
4 |
30 |
|
30 |
60 |
|
0 |
|
150 |
|
|
4 |
- |
|
D,E |
AB |
B |
AB |
||
5 |
90 |
|
120 |
120 |
|
90 |
|
60 |
|
|
- |
6 |
|
A,E |
AB |
A |
AB |
||
6 |
90 |
|
150 |
120 |
|
90 |
|
30 |
|
|
3 |
- |
|
B,E |
DE |
|
B |
AB |
|
7 |
0 |
|
60 |
60 |
|
0 |
|
120 |
|
|
- |
2 |
|
A,E |
DE |
|
A |
AB |
|
8 |
60 |
|
150 |
120 |
|
90 |
|
30 |
|
|
2 |
- |
|
D,E |
AB |
B |
AB |
||
9 |
30 |
|
120 |
150 |
|
0 |
|
60 |
|
|
- |
8 |
|
A,E |
DE |
|
A |
AB |
|
Таблица К3б (к рис. К3.5–К3.9)
Номер |
|
Углы градусы |
|
|
Дано |
|
|
Найти |
|
||||
усло- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω1, |
ε1, |
VB, |
aB, |
V |
ω |
a |
ε |
|
вия |
α |
β |
γ |
ϕ |
θ |
1/с |
1/с2 |
|
м/с2 |
то- |
зве- |
точ- |
зве- |
|
|
|
|
|
|
м/с |
чек |
на |
ки |
на |
|||
0 |
120 |
30 |
30 |
90 |
150 |
2 |
4 |
- |
- |
B,Е |
AB |
B |
AB |
1 |
0 |
60 |
90 |
0 |
120 |
- |
- |
4 |
6 |
A,E |
DE |
A |
AB |
2 |
60 |
150 |
30 |
90 |
30 |
3 |
5 |
- |
- |
B,E |
AB |
B |
AB |
3 |
0 |
150 |
30 |
0 |
60 |
- |
- |
6 |
8 |
A,E |
AB |
A |
AB |
4 |
30 |
120 |
120 |
0 |
60 |
4 |
6 |
- |
- |
B,E |
DE |
B |
AB |
5 |
90 |
120 |
90 |
90 |
60 |
- |
- |
8 |
10 |
D,E |
DE |
A |
AB |
6 |
0 |
150 |
90 |
0 |
120 |
5 |
8 |
- |
- |
B,Е |
DE |
B |
AB |
7 |
30 |
120 |
30 |
0 |
60 |
- |
- |
2 |
5 |
А,E |
AB |
A |
AB |
8 |
90 |
120 |
120 |
90 |
150 |
6 |
10 |
- |
- |
B,E |
DE |
B |
AB |
9 |
60 |
60 |
60 |
90 |
30 |
- |
- |
5 |
4 |
D,E |
AB |
A |
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. К3.0 |
Рис. К3.1 |
Рис. К3.2 |
Рис. К3.3 |
109 |
110 |
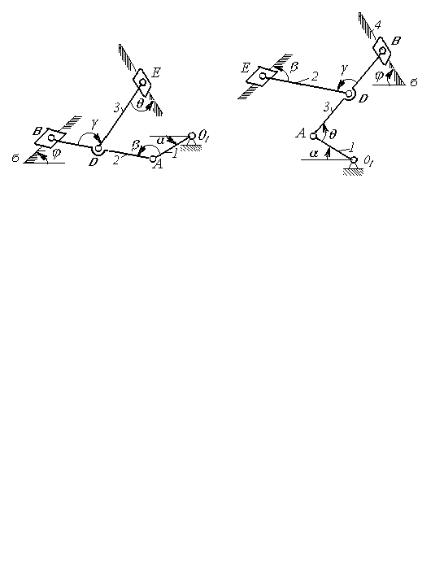
Рис. К3.4 |
Рис. К3.5 |
Рис. К3.6 |
Рис. К3.7 |
Рис. К3.8 |
Рис. К3.9 |
Задача К4
Прямоугольная пластина (рис. К4.0–К4.4) или круглая пластина радиуса R = 60см (рис. К4.5–К4.9) вращается вокруг неподвижной оси по закону ϕ = f1(t), заданному в таблице К4. Положительное направление отсчета угла ϕ показано на рисунках дуговой стрелкой. На рис. 0, 1, 2, 5, 6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 3, 4, 7, 8, 9 ось вращения ОО1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD (рис. 0–4) или по окружности радиуса R (рис. 5–9) движется точка M; закон ее относительного движения, т.е. зависимость S = AM = f2(t) (S выражено в сантиметрах, t –– в секундах), задан в таблице отдельно для рис. 0– 4 и для рис. 5–9; там же даны размеры b и . На рисунках точка M показана в положении, при котором S = AM > 0 (при S < 0 точка M находится по другую сторону от точки A).
Найти абсолютную скорость и абсолютное ускорение точки M в момент времени t1 = 1 с.
Указания. Задача К4 –– на сложное движение точки. Для ее решения воспользоваться теоремами о сложении скоростей и о сложении ускорений. Прежде, чем производить все расчеты, следует по условиям задачи определить, где находится точка M на пластине в момент времени t1 = 1 с, и изобразить точку именно в этом положении (а не в произвольном, показанном на рисунках к задаче).
В случаях, относящихся к рис. 5–9, при решении задачи не подставлять числового значения R, пока не будут определены положение точки M в момент времени t1 = 1 с и угол между радиусами CM и CA в этот момент.
111 |
112 |
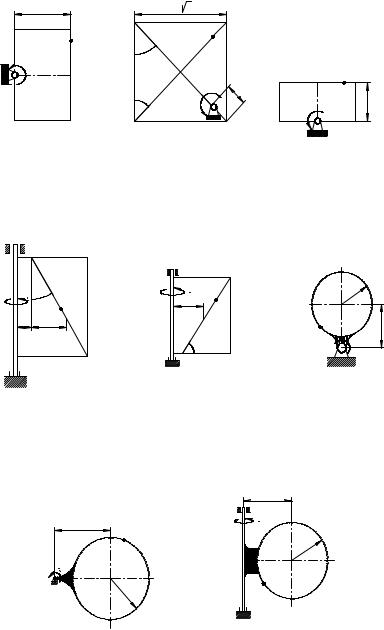
Таблица К4
Номер условия |
Для всех |
|
Для рис. 0–4 |
Для рис. 5–9 |
|
|
|
|
|||||||||||||
ϕ = f1 (t) |
см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
рисунков |
t , |
s = AM = f2 (t) |
|
|
|
s = AM = f2 (t) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
0 |
4(t2 −t) |
|
12 |
50(3t |
−t 2 ) −64 |
|
R |
π R(4t2 |
−2t3 ) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
1 |
3t 2 |
−8t |
16 |
40(3t3 |
−t 4 ) −32 |
4 |
R |
π R(2t2 −t3 ) |
|||||||||||||
|
3 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
6t 3 |
|
−12t 2 |
10 |
80(t 2 |
−t) +40 |
|
R |
π R(2t2 |
−1) |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
t 2 |
|
−2t3 |
16 |
60(t 4 −3t 2 ) +56 |
|
R |
π R(3t |
−t2 ) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
4 |
10t 2 |
−5t3 |
8 |
80(2t 2 |
−t 3 ) −48 |
|
R |
π |
R(t 3 |
−2t |
|
) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
5 |
2(t 2 |
−t) |
20 |
60(t 3 −2t 2 ) |
|
R |
π R(t3 −2t) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
6 |
5t −4t |
2 |
12 |
40(t |
2 |
−3t) +32 |
|
3 R |
π |
R(t |
3 |
−2t |
2 |
) |
|||||||
|
|
|
4 |
|
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
7 |
15t |
|
|
−3t3 |
8 |
60(t |
|
−t 3 ) +24 |
|
R |
π R(t |
|
−5t2 ) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
8 |
2t3 −11t |
10 |
50(5t 3 −t |
) −30 |
|
R |
π R(3t2 −t |
) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
9 |
6t |
2 |
−3t |
3 |
20 |
40(t −2t |
3 |
) −40 |
|
3 R |
π |
R(t |
|
−2t |
2 |
) |
|||||
|
|
|
4 |
|
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 b |
|
5 b 2 |
|
|
|
D |
|
D |
|
|
|
|
M |
|
|
||
M |
|
|
|
||
Е |
|
|
|
||
|
|
|
|
||
|
5 |
|
|
|
|
f |
4 |
A |
|
|
|
|
|
|
|||
|
|
|
|
||
A |
|
B |
A |
M D |
|
O |
45 |
b |
|
|
|
f O |
f |
3 b |
|||
|
Е |
||||
B |
|
|
O |
|
|
B |
|
|
|
||
Рис. К4.0 |
Рис. К4.1 |
|
|
||
|
|
|
Рис. К4.2 |
|
O1 |
|
|
|
|
|
|
|
|
|
|
D |
|
O1 |
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
Е |
|
|
f |
|
|
|
R |
|
|
30 |
|
|
4 b |
M |
DC |
C |
|
|
|
|
M |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
b |
2 b |
A |
|
A |
|
|
|
A |
2 |
|
|
|
M |
|
|||||
|
|
|
|
|
|
|
|||
|
|
|
|
6 |
|
|
|
f |
|
|
|
|
O |
0 |
|
O |
|
|
|
|
|
|
|
|
|
|
|
||
O |
|
B |
Е |
|
|
|
|
||
|
|
|
B |
|
|
|
|
|
|
Рис. К4.3 |
Рис. К4.4 |
Рис. К4.5 |
|
|
|
O1 |
2 l |
|
|
i |
|
j |
|
|
|
D M |
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
A |
|
f |
|
|
|
C |
|
|
C |
A |
|
|
|
|
|
M |
|
||
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
D |
|
|
|
|
|
|
|
|
Рис. К4.6 |
|
Рис. К4.7 |
|
|
|
|
|
|
|
113 |
114 |
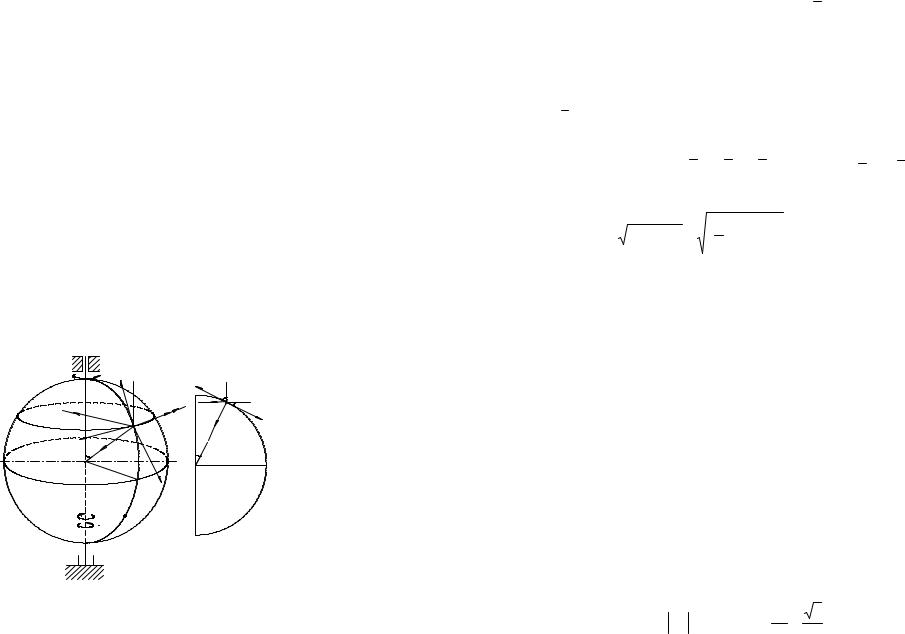
Пример К4. Шар радиуса R (рис. К4, а) вращается вокруг своего диаметра AB по закону ϕ = f1(t) (положительное направление отсчета угла ϕ показано на рис. К4, а дуговой стрелкой). По дуге большого круга («меридиану») ADB движется точка M по закону S = AM = f2(t); положительное направление отсчета s от A к D.
Д а н о : R = 0,5 м, ϕ= 2t |
3 |
−4t |
2 |
, |
|
πR |
2 |
) (ϕ –– в ра- |
|
|
s = |
(7t −2t |
|
||||
|
|
|
|
|
|
6 |
|
|
дианах, s –– в метрах, t –– в секундах).
О п р е д е л и т ь : ϑаб и aаб в момент времени t1 = 1 с. Решение. Рассмотрим движение точки М как сложное, считая ее
движение по дуге ADB относительным (AB –– относительная траектория точки), а вращение шара –– переносным движением. Тогда
абсолютная скорость |
|
|
аб |
и абсолютное ускорение ааб |
|
|||||
ϑ |
точки опре- |
|||||||||
делятся по формулам: |
|
|
|
|
||||||
|
|
аб = |
|
от |
+ |
|
пер , ааб = аот + апер + акор , |
(1) |
||
|
ϑ |
ϑ |
ϑ |
|||||||
где, в свою очередь, аот = аотτ + аотn , апер = аперτ +аперn .
f |
|
- |
|
|
B |
qоt |
z |
|
|
|
|
y |
n |
h |
|
- |
|
||
а |
|
|
|
пер |
|
|
|
- |
|
|
q |
0 |
- t |
пер 30 |
|
|
|
|
aot |
C
D
w
e
M
A |
|
|
|
- |
|
z |
|
|
|
|
|
qot |
|
|
||
|
|
|
|
60 |
0 |
|
|
- |
а-пеtр |
B |
|
- n h |
M1 |
30 |
o - t |
акор |
|
x |
y |
aпер |
|
|
aot |
M1 |
|
|
|
- n |
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
оt |
|
|
|
|
|
|
30 0 |
|
|
|
|
|
|
C |
|
|
|
|
D |
- t |
|
|
|
|
|
|
|
aоt |
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
а) |
б) |
Рис.К4
Направление акор найдем, спроектировав вектор ϑаб на плоскость, перпендикулярную оси вращения (проекция направлена так же, как
вектор аперn ), и повернув затем эту проекцию в сторону ω, т. е. по ходу часовойстрелки, на900. Иначенаправление акор можнонайти, учтя, что
акор = 2(ω×ϑот ). Изображаемвектор акор нарис. К4, а. Теперь можно вычислить значения υаб и ааб.
4. Определение υаб. Так как ϑаб =ϑот +ϑпер , а векторы ϑот и ϑпер взаимноперпендикулярны(см. рис. К4, а), товмоментвремениt1 = 1 с
2 |
2 |
= |
|
π 2 |
+(0,5) |
2 |
= 0,93 |
ϑаб = ϑот |
+ϑпер |
|
|
|
|||
|
|
|
|
4 |
|
|
м/с. |
|
|
|
|
|
|
|
|
5. Определение ааб. По теореме о сложении ускорений |
|||||||
а = аτ |
+аn |
+аτ |
+аn |
+а |
(7) |
аб от |
от |
пер |
пер |
кор . |
Для определения ааб проведем координатные оси M1xyz (см. рис.
К4, а) и вычислим проекции вектора ааб на эти оси. Учтем при этом, что векторы аперτ и акор лежат в проведенной оси x, а векто-
ры аотτ , аотn , аперn расположены в плоскости дуги ADB, т.е. в плос- кости M1yz (см. рис. К4, б). Тогда, проектируя обе части равенства
(7) на координатные оси и учтя одновременно равенства (3), (5), (6), получим для момента времени t1 = 1 с
|
|
|
aабx = аперτ |
+ акор =1+ 2,72 = 3,72 м/с2; |
|
|||||||||
a |
= а |
n |
+а |
n |
cos 60°− а |
τ |
cos30° =1 |
+ |
π2 |
− |
3 |
= 0,71 |
2 |
|
пер |
от |
от |
|
|
м/с ; |
|||||||||
абy |
|
|
|
|
|
|
16 |
|
6 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
115 |
116 |
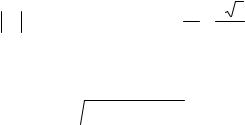
a |
|
= −а |
τ |
cos 60°−а |
n |
|
π2 |
+ |
π 3 |
|
= −1,59 |
2 |
абz |
от |
от |
cos30° = − |
|
|
|
м/с . |
|||||
|
|
|
|
6 |
|
16 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Отсюда находим значение ааб в момент времени t1 = 1 с:
aаб =  aаб2 x +aаб2 y +aаб2 z = 4,1 м/с2.
aаб2 x +aаб2 y +aаб2 z = 4,1 м/с2.
Ответ: ϑ аб = 0,93 м/с; ааб = 4,1 м/с2.
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ КОНТРОЛЬНЫХ РАБОТ
ДЛЯ СТУДЕНТОВ ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ
_________________________________________________
1. Каждая контрольная работа выполняется в отдельной тетради. На обложке указываются: название дисциплины, номер работы, фамилия и инициалы студента, учебный шифр (шифр зачетной книжки), группа.
При чтении текста каждой задачи необходимо учесть следующее. Большинство рисунков дано без соблюдения масштаба. На рисунках к задачам все линии, параллельные строкам, считаются горизонтальными, а перпендикулярные строкам –– вертикальными. Это в тексте задач специально не оговаривается. Также без оговорок считается, что все нити (веревки, тросы) являются нерастяжимыми и невесомыми; нити, перекинутые через блок, по блоку не скользят, катки и колеса (в кинематике и динамике) катятся по плоскостям без скольжения. Все связи, еслинесделанодругихоговорок, считаютсяидеальными.
Когда тела на рисунке пронумерованы, то в тексте задач и в таблице все величины, относящиеся к ним, должны иметь соответствующие номера.
Из всех пояснений в тексте задачи обращайте внимание только на относящиеся к вашему варианту, т. е. к номеру вашего рисунка или вашего условия в таблице.
Методические указания по решению задач, входящих в контрольные задания, даются для каждой задачи после изложения ее текста под рубрикой «Указания», затем дается пример решения аналогичной задачи. Цель примера — разъяснить ход решения, но не воспроизвести его полностью. Поэтому в ряде случаев промежуточные расчеты опускаются. Но при выполнении задания все преобразования и числовые расчеты должны быть обязательно последовательно проделаны с необходимыми пояснениями; в конце должны быть даны ответы.
117 |
118 |
2. Решение каждого задания обязательно начинать на развороте |
обложке запись «К защите не допускается» (с соответствующим |
тетради (на четной странице, начиная со второй). Перед выполне- |
комментарием). |
нием задания необходимо записать его условие, выбранные в соот- |
8. Запрещается стирать или заклеивать отмеченные преподава- |
ветствии с вариантом исходные данные, изобразить расчетную |
телем ошибки. |
схему. Расчетная схема должна быть вычерчена в масштабе, с ука- |
9. Работы, оформленные небрежно и без соблюдения предъяв- |
занием всех размеров, числовых данных и осей, используемых в |
ляемых к ним требований, а также работы, выполненные не по сво- |
расчете. Нагрузки следует показать в соответствии с их дей- |
ему варианту, не рассматриваются и не засчитываются, возвраща- |
ствительными направлениями. |
ются для переделки. К работе, высылаемой на повторную проверку |
3. При выполнении задания сначала надо наметить ход решения |
(если она выполнена в другой тетради), должна обязательно прила- |
и те допущения, которые могут быть положены в его основу, а за- |
гаться незачтенная работа. |
тем произвести расчет; при этом все необходимые вычисления (по |
Выбор варианта |
возможности) сначала проделать в общем виде, обозначая все дан- |
|
ные и искомые величины буквами, после чего вместо буквенных |
Студент выбирает номер рисунка по предпоследней цифре |
обозначений поставить их числовые значения и найти результат. |
|
Везде необходимо придерживаться стандартных обозначений. Рас- |
учебного шифра, а номер условия в таблице –– по последней. |
четы должны быть выполнены в определенной последовательности, |
|
теоретически обоснованы и сопровождены пояснительным текстом. |
|
Решение записывается подробно и аккуратно со всеми вычисле- |
|
ниями, вспомогательными чертежами и пояснениями. При выпол- |
|
нении расчетов необходимо указывать литературу с отметкой стра- |
|
ниц и таблиц, откуда взяты расчетные формулы, расчетные напря- |
|
жения и другие величины. |
|
4. Все расчеты должны производиться в единицах СИ. Вычисле- |
|
ния следует вести с обычной в технических расчетах точностью |
|
(до трех значащих цифр после запятой). |
|
5. Выполненные контрольные работы должны быть высланы в |
|
университет на рецензирование. Работы, поступившие на рецензи- |
|
рование позже установленного срока, рассмотрению не подлежат. |
|
6. После рецензирования контрольной работы необходимо вне- |
|
сти в соответствии с замечаниями рецензента требуемые исправле- |
|
ния (не в тексте решения, а в конце тетради на чистых листах после |
|
заголовка «Исправления к заданию»). |
|
7. Если количество замечаний невелико и ошибки, допущенные |
|
студентом при выполнении контрольной работы, несущественны, |
|
т.е. требуется незначительная ее доработка, рецензент делает на |
|
обложке запись «К защите допускается». |
|
В противном случае, если требуется существенно переработать |
|
контрольную работу или переписать ее заново, рецензент делает на |
|
119 |
120 |
