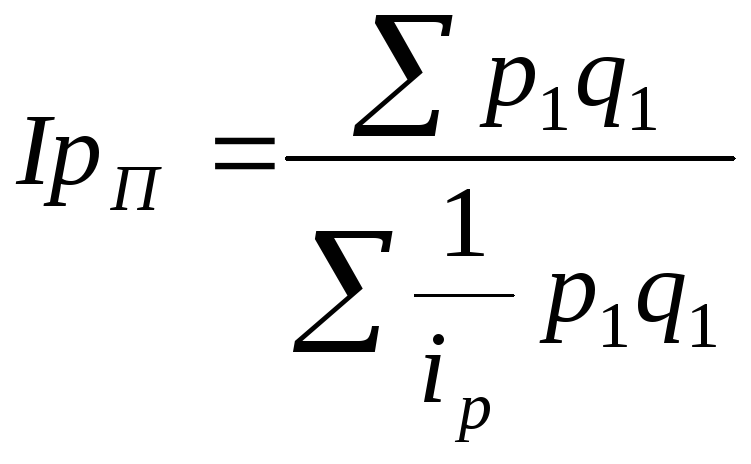Тема 4. Ряды динамики

Рядами динамики называют показатели, уровни (у) которых представляют изменение явления (численности, объемов) во времени.

Необходимо четко представлять себе виды рядов динамики, расчет среднего уровня в зависимости от вида ряда динамики, а также систему показателей анализа динамических рядов (2, с. 115-206; 3, с. 101-118) Средний уровень ряда исчисляется:

- в интервальном, периодическом ряду динамики по формуле средней арифметической:

,

где - средний уровень;

- сумма уровней ряда;

п - число уровней ряда.

- в моментном динамическом ряду с равными интервалами времени между датами средний уровень ряда вычисляется по формуле средней хронологической (2, с. 165)

где y₁, y₂, … y_n – уровни моментного ряда динамики (1-й, 2-й, ... n-й);

n - число уровней.

Следует знать, что система показателей рядов динамики может быть исчислена базисным (сравнения последующего уровня – у_i с начальным уровнем – y₁) и цепным (сравнения каждого последующего уровня с предыдущим – y_i-1) (2, с. 161-165; 3, с.104-109) методами.

Формулы расчета показателей анализа рядов динамики изложен в таблице.

Таблица 1.

Показатели анализа рядов динамики	Формулы расчета
	базисным методом	ценным методом
1. Абсолютное изменение	Δб=yi – y1	Δц = yi – yi-1
2. Темпы роста
3. Коэффициенты роста
4. Темпы прироста	tб = Тб - 100,0	tц = Тц - 100,0

Особое внимание следует обратить студентам на расчет таких показателей анализа рядов динамики:

1) абсолютное значение 1% прироста (снижения)

или ;

2) средний абсолютный прирост (снижение)

где - средний абсолютный прирост (уменьшение);

y_i-1 - любой последующий уровень ряда, включая и первый;

у_n - последний уровень ряда.

3) средний годовой коэффициент () или темп () изменения за период, применяя среднюю геометрическую формулу;

, откуда =· 100,

а потом исчисляют среднегодовой темп прироста (снижения) по формуле:

Тема 5. Индексы

При изучении этой темы учащиеся должны четко представлять, что индексы - это особый вид относительных величин. Понятие, принципы классификации, виды и методы расчета индексов довольно полно изложены в учебной литературе (2, с. 206-237; 3, с. 121-138).

При исчислении индексов, характеризующих динамику явлений, символам показателей счетного периода придается под строчкой знак "l" (например, р₁ - цена за единицу товара отчетного периода; q₁ - количество отдельных видов товаров отчетного периода), а базисного периода - знак "0" (p₀ - цена за единицу товара базисного периода; q₀ - количество отдельного вида товара базисного периода). Исходя из этого p₁q₁ и p₀q₀ - товарооборот, стоимость товара соответственно в отчетном и базисном периодах.

Индивидуальные индексы исчисляются по формулам:

количества ; цен .

Студент должен знать, что при расчете общих индексов сопоставляются суммы стоимостей - . Расчет общих индексов ведется по формулам:

- общего стоимостного индекса или индекса товарооборота в действующих ценах (Ipq).

;

разность между числителем и знаменателем индекса дает абсолютное изменение стоимости или товарооборота в целом (Δpq):

;

- общего индекса физического объема или товарооборота в сопоставимых ценах (Iq):

,

где - сумма стоимости, товарооборота отчетного периода в сопоставимых ценах (р₀);

разность между числителем и знаменателем индекса дает абсолютное изменение стоимости или товарооборота за счет физического объема, количественного фактора [Δpq(q)]

;

общего индекса цен (Ip)

Паоше (I система индексов)

;

разность между числителем и знаменателем индекса дает абсолютное изменение стоимости или товарооборота за счет цен, качественного фактора [Δpq(p)]

Для проверки расчетов используют формулу:

Δpq = Δpq(p) + Δpq(q)

В учебной литературе приведены формулы и расчет этих индексов на примерах (2, с. 207-219; 3, с. 123-129).

Общий индекс цен (Ip) может быть рассчитан и по формуле Ласпейреса (II система индексов)

.

Рассмотренные индексы называют общими индексами в форме агрегатной. Но в практике экономических расчетов чаще применяют общие индексы в форме средней, что связано с информационным обеспечением. Общие индексы в форме средней - это общие агрегатные индексы, преобразованные с помощью индивидуальных (2, с 219-224; 3, с. 129-131).

Необходимо знать, что общие индексы в форме средней аналогичны по своему экономическому содержанию индексам агрегатным.

Покажем в таблице 2 основные формулы общих индексов в форме средней и методы их получения.

Таблица 2.

	Агрегатная Форма	Индивидуальный индекс	Общие индексы в форме средней
Индекс цен (Ip) Пааше		ip = p1: p0 , откуда	гармонической
Ласпейрса		ip = p1: p0 , откуда p1 = ipp0	арифметической
Индекс физического объема (Iq)		ip = p1: p0 , откуда	смешанной
		iq = q1: q0 , откуда q1 = iqq0	арифметической

Особое внимание следует уделить системе индексов в анализе динамики средних показателей (2, с. 224-228; 3, с. 131-132). Рассмотреть принципы построения этой системы можно на примере анализа динамики средних цен. Система в этом случае имеет вид:

Для их расчета исчисляют предварительно средние цены () по арифметической взвешенной:

средняя цена

- базисного периода ;

- отчетного периода ;

- условная .

Используя эти расчеты, студент легко исчислит каждый индекс из приведенной системы по формулам:

;

;

.

Приведенная система индексов дает возможность определить абсолютное изменение цен по формулам

в целом , в том числе эа счет изменения:

1) цен у отдельных продавцов ;

2) структуры реализованных товаров

Важным для рассмотрения в этой теме является вопрос взаимосвязи индексов, которая опирается на следующее: взаимосвязь абсолютных показателей (например, р × q = pq ), правомерна для взаимосвязи относительных показателей, индексов этих же явлений; т.е.

, откуда или

Значение принципов взаимосвязи индексов дает возможность широко применять эти формулы на практике для расчета динамики, изменения неизвестного показателя (2, с. 228-232; 3, с. 132-134)

Рассмотренные нами общие индексы (I_p, I_q, и I_pq) относятся к I системе взаимосвязанных индексов или системе Пааше.