3. Теплота растворения.

При растворении твёрдых нелетучих веществ проявляется тепловой эффект . Правило Бабо точно, когда.

Когда , необходимо учитывать поправку проф. Стабникова(приводится в таблицах в зависимости отP_A и ''С'').

При >0 поправка прибавляется, при<0 – вычитается из температурной депрессии, рассчитанной по правилу Бабо.

Многократное выпаривание

Рассмотрим многократное выпаривание на прямоточной установке, содержащей ''n'' корпусов. Все полученные уравнения будут справедливы и для однократного выпаривания, когда n=1.

Схема установки представлена на рис.105.

Рис.105. Схема прямоточной выпарной установки, состоящей из ''n'' корпусов.

1-греющий пар, 2-конденсат, 3-исходный раствор, 4-вторичный пар,

5-вторичный пар в барометрический конденсатор, 6-упаренный раствор.

G, D, W – расходы раствора, греющего и вторичного пара, кг/с;

J_г, J – энтальпии греющего и вторичного пара, кДж/кг;

С, С' – теплоёмкость раствора и конденсата, ;

t, - температура раствора и конденсата, ;

b – концентрация раствора, % масс.

1. Материальный баланс.

а) Для всей установки по всему продукту:

или (102)

где - общий расход вторичного пара.

б) Для всей установки по растворённому веществу:

; (103)

Откуда общий выход вторичного пара

(104)

Концентрация раствора для n-ого и любого корпуса:

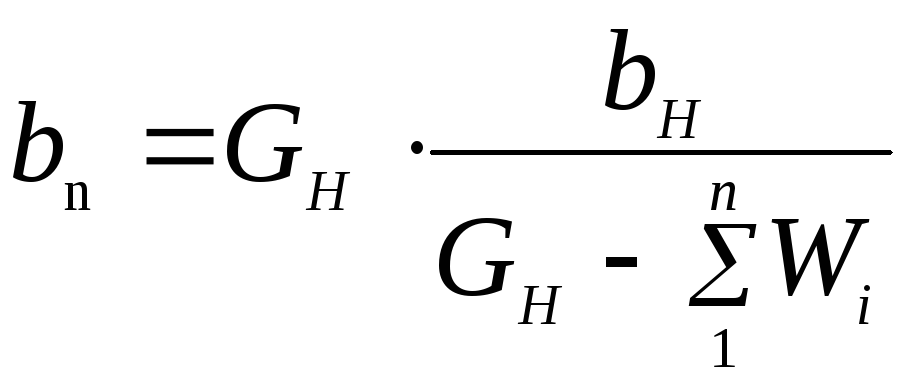(105)

в) Распределение вторичного пара по корпусам.

В прямотоке раствор поступает в следующий корпус с более высокой температурой и вносит дополнительное количество тепла. За счёт этого происходит самоиспарение раствора и вторичного пара образуется больше. Для 3-х корпусной установки хорошо подтверждается отношение, полученное на основе опытных данных:

(106)

Выпаривание с отбором экстра-пара в настоящее время практически не применяется.

2. Тепловой баланс.

Тепловой баланс необходим для расчёта:

А. Расхода греющего пара на первый корпус ;

В. Уточнения распределения вторичного пара по корпусам ();

С. Определения тепловых нагрузок каждого корпуса ().

По общему методу И.А. Тищенко при составлении теплового баланса вводятся следующие допущения:

а) Пренебрегаем потерями в окружающую среду, .

б) Пренебрегаем теплотой концентрирования раствора, .

в) Полагаем, что отсутствует охлаждение раствора при переходе из одного корпуса в другой ().

г) Отсутствует переохлаждение конденсата водяного пара ().

д) Выражение заменяется на приближённое значение

; где

Это связано с трудностями определения теплоёмкости раствора . Теплоёмкость разбавленного раствора (до 10% масс.) определяется по приближённой формуле

(108)

Баланс тепла:

1-й корпус

2-й корпус

………………………………………………………………………………………...

n-й корпус

Из последнего уравнения получаем количество вторичного пара для n-ого корпуса:

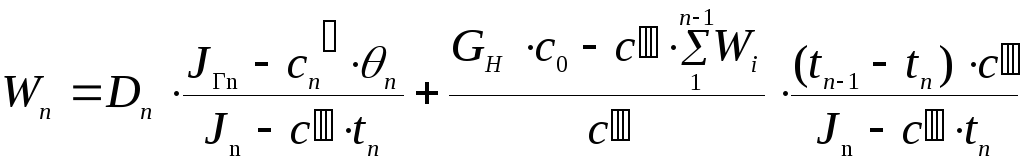
делим и умножаем на

Обозначим:

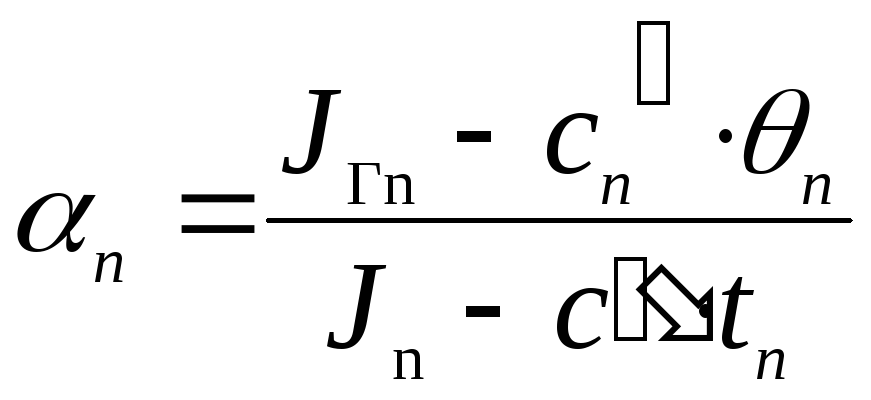- коэффициент испарения, показывает количество вторичного пара, образующееся за счёт теплоты 1 кг греющего пара; обычно =0.92-0.99.

- коэффициент самоиспарения, показывает количество вторичного пара, образующееся за счёт теплоты 1 кг поступающего раствора; обычно =сотые доли.

Тогда: (109)

Уравнение (109) для 3-х корпусной прямоточной выпарной установки (без экстра-пара) принимает вид:

1-й корпус

2-й корпус (В)

3-й корпус

Складываем:

Откуда расход греющего пара на первый корпус

(А)

где

Тепловые нагрузки на каждый корпус:

где