
Блок3
.pdf
Лекция 5Б
1.Преобразование проекций и его значение в начертательной геометрии. Четыре ос-
новных задачи преобразования проекций.
2.Плоскопараллельное перемещение – один из способов преобразования проекций.
Решение четырех основных задач способом ППП.
3.Вращение вокруг оси перпендикулярной плоскости проекций – частный случай ППП.
4.Вычисление точки пересечения прямых и прямой с плоскостью.
ПОЛОЖЕНИЯ ГЕОМЕТРИЧЕСКИХ ОБРАЗОВ ПРИ КОТОРЫХ РАССТОЯ НИЯ И УГЛЫ НЕ ИСКАЖАЮТСЯ НА ПЛОСКОСТИ ПРОЕКЦИЙ.
Если прямые и плоскости занимают частное положение относительно плоскости проекций (параллельны или перпендикулярны плоскости проекций), то многие длины,
площади, расстояния и углы не искажаются. Следовательно, если необходимо опре-
делить подобные метрические характеристики, то можно привести преобразованием проекций геометрические формы к нужному частному положению, при котором нужную метрическую характеристику определяют простым измерением на той плоскости про-
екций, где эта характеристика не искажается. Приведем положения некоторых геомет-
рических форм с не искажающимися метрическими характеристиками (рис. 1).
А2 |
С2 |
а2 |
b2 |
|
n2 |
а2 |
А1 |
В2 |
|
m2 |
p2 |
||
С1 |
|
|
|
|||
|
|
|
|
n1 |
d0 |
|
|
|
|
ϕ |
|
||
|
|
a1 |
|
|
p1 |
|
|
|
|
b1 |
m1 |
d0 |
a1 |
|
В1 |
Н. в. прямых а и b |
d0 – расстояние |
90° |
||
Н. в. треугольника АВС с не |
|
|||||
искаженными его сторонами |
та угла ϕ между ними. |
между m и n. |
|
|
d0 - расстояние |
|||||||||||||||||||||||
углами и высотами. |
|
|
C2 |
A2 |
|
|
|
|
|
|
|
C2 |
С2 |
|
В2 между а и р. |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
K2 |
|
A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А2 |
|
ϕ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
A2 |
|
|
|
|
B2 |
|
|
|
|
D2 |
|
|
B2 |
|
|
|
|
|
|
|
|
|
С1 |
|
|
|
ϕ - угол наклона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
d0 |
|
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
K |
1 |
А |
1 |
|
|
|
|
плоскости АВС к |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
A1 |
|
|
|
|
|
|
|
|
D1 |
A1 |
|
|
|
|
|
|
|
|
d0 |
|
|
|
|
горизонтальной |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
90° |
|
|
|
|
m1 A1≡B1 |
ϕ0 |
|
C1 |
|
|
B1 |
|
|
|
|
C1 |
В1 |
|
|
плоскости проекций |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
d0 –расстояние от ϕ0 – угол между |
|
|
d0 – расстояние от точки |
|
|
|
|
|
||||||||||||||||||||
от А до прямой m гранями АВС и ABD |
|
|
К до плоскости АВС |
|
|
|
|
Рис. 1 |
||||||||||||||||||||
Для приведения геометрических форм из общего в необходимое частное поло-
жение используют способы преобразования проекций. К способам преобразования
проекций относятся:
∙Плоско параллельное перемещение (сокращенно ППП).
∙Вращение вокруг осей перпендикулярных плоскостям проекций.
∙Замена плоскостей проекций (сокращенно ЗПП).
∙Вращение вокруг линий уровня.
∙Способ совмещения.
∙Способ вспомогательного проецирования.
Способы ППП и ЗПП являются основными способами преобразования проекций, а ос-
тавшиеся четыре – дополнительными. ППП и ЗПП являются равноценными по возмож-
ностям, которые они предоставляют при решении всевозможных задач начертатель-
ной геометрии. Дополнительные способы применяются более специализировано, так как каждый из них наиболее эффективен при решении своего специального класса за-
дач. Эта специализация будет выделена при изложении каждого из способов преобра-
зования проекций.
ЧЕТЫРЕ ОСНОВНЫЕ ЭТАПЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ.
Для успешного решения задач начертательной геометрии с применением спосо-
бов преобразования проекций возникла необходимость выделить некоторые задачи преобразования геометрических форм и выделить для них личные обозначения (дать им имена):
1. Задача №1. Линия натуральная (ЛН):
Приведение прямой из общего положения в положение прямой уровня. 2. Задача №2. Линия точка (ЛТ):
Приведение прямой в проецирующее положение. 3. Задача №3. Плоскость линия (ПЛ):
Приведение плоскости из общего положения в проецирующее. 4. Задача №4. Плоскость натуральная (ПН):
Приведение плоскости в положение плоскости уровня.
Методика решения задач начертательной геометрии с использованием преобразования проекций
Чтобы использовать преобразование проекций для решения конкретно за-
данной задачи, необходимо
∙представить в каком частном положении должны находится геометриче-
ские объекты этой задачи для того, чтобы ответ задачи можно получить на одной из проекций очень просто (например, применяя простое измерение).
Некоторые из подобных положений приведены на рисунке (рис. 1).
∙Отметить какое из четырех положений ЛН, ЛТ, ПЛ или ПН необходимо для непосредственного решения задачи.
∙Преобразованием проекций привести задачу к этому частному положе-
нию. Выделить на преобразованной проекции ответ задачи.
ПЛОСКО ПАРАЛЛЕЛЬНОЕ ПЕРЕМЕЩЕНИЕ (ППП) - ОДИН ИЗ СПОСОБОВ
ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ.
Если геометрический объект перемещать в системе плоскостей проекций так,
чтобы одна из координат каждой точки его не изменяла своей величины, то такое пе-
ремещение называется плоско параллельным. Каждая точка объекта перемещается по некоторой траектории расположенной в плоскости уровня (горизонтальной или фрон-
тальной). Соответственно этому различают горизонтальное плоско параллельное пе-
ремещение (ГППП) и фронтальное плоско параллельное перемещение (ФППП). Для решения любой из четырех основных задач преобразования проекций достаточно этих двух видов ППП. Если речь идет о перемещении объекта, то предполагается, что он при этом не допускает деформаций, т. е. расстояния между точками объекта не изме-
няются при перемещении. Поскольку в начертательной геометрии объекты простран-
ства изображаются на плоском листе чертежа с помощью системы двух ортогональных проекций (системы Г. Монжа), то для описания ППП необходимо определить способы перемещения проекций при ГППП и ФППП.
ПЕРЕМЕЩЕНИЕ ПРОЕКЦИЙ ПРИ ГППП
При ГППП высоты точек перемещаемого объекта не изменяются, следователь-
но, каждая точка его фронтальной проекции движется по линиям параллельным оси проекций. Не меняя высоты точек мы не сможем изменить вида горизонтальной проек-
ции, только положение горизонтальной проекции может меняться перемещаясь согла-
совано с движением самого объекта в пространстве. Следовательно, чтобы произвести горизонтальное плоскопараллельное перемещение необходимо:
1.Не изменяя формы горизонтальной проекции, переместить ее в нужное место
(допустим, как параллельный перенос этой проекции, так и ее поворот).
2.Достроить фронтальную проекцию каждой точки объекта, не изменяя высот.
Пример ГППП. Прямую АВ переместить горизонтально плоскопараллельно так, чтобы она оказалась фронтальной прямой уровня.
РЕШЕНИЕ |
|
|
В2 |
|
|
|
В21 |
|
|
|
|
|
|
|
|
Горизонтальную проекцию А1В1 (рис. 2) |
А2 |
|
А21 |
|
|
|
|
|
|
|
|
|
|
||
перемещаем на свободное место чертежа пово |
Х12 |
|
А11 |
|
|
|
В11 |
рачивая ее до положения параллельного оси |
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
||||
проекций Х12. По линиям связи фиксируем |
А1 |
|
|
|
А1В1 = А11В11 |
||
|
|
||||||
фронтальные проекции точек А21В21. |
|
|
|
|
|
|
|
|
|
|
В1 |
|
Рис. 2 |
||
ПЕРЕМЕЩЕНИЕ ПРОЕКЦИЙ ПРИ ФППП
При фронтальном плоскопараллельном перемещении неизменными остаются глубины точек. При ФППП фронтальная проекция объекта не меняясь по величине, копирует движение его, а горизонтальная проекция каждой его точки перемещается по линиям параллельным оси проекций Х12.
Пример ФППП: Плоскость α(АВС) из общего положения перевести в горизонтально проецирующее положение.
Плоскость является горизонтально проецирующей, если она содержит горизонтально проецирующую прямую. Фронтальную прямую можно одним ФППП перевести во фронтально проецирующее положение. Следовательно, для решения задачи необходимо в плоскости провести фронталь, которую, совместно с плоскостью, переводим во фронтально проецирующее положение (рис. 3). В нашем примере фронталь BD плоскости АВС фронтальным плоско параллельным перемещением спроецирована в точку В11 ≡ D11, тогда плоскость треугольника проецируется в линию A11B11C11.
Подавляющее большинство задач кур |
|
|
|
||
са начертательной геометрии используют че |
С2 |
А21 |
D21 |
||
|
|
|
|||
тыре основных задачи преобразования про- |
D2 |
|
C21 |
||
A2 |
|
|
|||
|
|
|
|
||
екций. Умение решать эти задачи позволит |
|
B2 |
|
||
|
|
|
|
||
значительно расширить возможности инже- |
A1 |
A11 |
B21 |
||
|
|
||||
нера. Легко заметить, что задача №1(ЛН - ли |
|
|
B11 ≡ D11 |
||
ния натуральная) рассмотрена нами в качес |
D1 |
B1 |
|||
|
|||||
тве примера (рис. 3), А21В21 – натуральная ве |
|
|
|
||
личина отрезка АВ. Следующий пример (рис. |
C1 |
|
|
||
|
|
|
C11 |
||
3) демонстрирует задачу №3 (ПЛ - плоскость |
ФППП |
|
|||
|
|
||||
|
|
|
|
||
линия). |
|
|
|
Рис. 3 |
|
|
|
|
|
||
Две другие задачи (ЛТ и ПН) требуют |
|
|
|
||
предварительного выполнения рассмотренных нами задач, только второе плоско па- |
|||||
раллельное перемещение позволит их решить. |
|
|
|
||
А2 |
А21 |
В21 |
А22 ≡ В22 |
||
|
|||||
|
В2 |
Задача ЛТ |
|
В12 |
|
|
|
|
|
||
В1 |
А11 |
|
|
|
|
|
Задача ЛН |
В11 |
|
|
|
А1 |
|
|
|
||
А2В2 = А21В21; А11В11 = А12В12 – натуральная величина АВ. |
А12 |
|
|||
|
|
|
Рис. 4 |
||
|
|
Задача ПН |
|
|
|
Задача ПЛ
Плоскость треугольника с помощью горизон- |
|
тали проецируется в линию (ПЛ), а затем в |
|
натуральную величину (ПН). |
Рис. 5 |
ВРАЩЕНИЕ ВОКРУГ ОСИ ПЕРПЕНДИКУЛЯРНОЙ ПЛОСКОСТИ ПРОЕКЦИЙ - ЧА-
СТНЫЙ СЛУЧАЙ ПЛОСКО ПАРАЛЛЕЛЬНОГО ПЕРЕМЕЩЕНИЯ
Если необходимо определить натуральные величины отрезков выходящих из одной точки, то удобно воспользоваться способом вращения вокруг оси перпендику-
лярной плоскости проекций. Этот способ теоретически ничем не отличается от ППП,
траектория движения при этом будет окружность.
Задача. Определить натуральные величины отрезков SA, SB, SC.
|
|
|
S2 |
н. в. SA |
|
||
|
|
|
A2 |
н.в.SB |
A21 |
|
|
|
|
|
|
|
н.в. SC |
||
|
|
|
B2 |
B21 |
|
||
Решение задачи понятно из |
|
C21 |
|||||
|
|
|
C2 |
S1 |
|
||
рисунка (рис. 6). Способ вращения |
|
|
|
||||
|
B11 |
A11 |
C11 |
||||
|
|
|
A1 |
||||
применяется |
при |
построении |
S1A1 = S1A11; S1B1 = S1B11; |
||||
|
|||||||
|
|
|
B1 |
S1C1 = S1C11. |
|||
разверток пирамид. |
|
C1 |
|
|
Рис. 6 |
||
|
|
|
|
||||
ВЫЧИСЛЕНИЕ ТОЧКИ ПЕРЕСЕЧЕНИЯ ПРЯМОЙ С ПЛОСКОСТЬЮ |
|
||||||
Вычисление точки пересечения двух прямых и точки пересечения прямой с плоскостью – важнейшие позиционные задачи курса начертательной геометрии. Они,
как составные части, входят в решение многих задач. Пересечение прямых в курсе рассматриваются или в плоскостях проекций, или в плоскостях уровня. Следовательно прямые не могут скрещиваться (точки, определяющие прямые, задаются двумя коор-
динатами из трех). Рассмотрим этот случай пересечения прямых АВ и СD. |
|
|||||||||||
Через площади ориентированных треугольников АСD |
D |
В |
||||||||||
BCD определяем отношение АК/ВК. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
К |
||||
Введем обозначения: |
|
x A |
yA |
1 |
|
|
xB |
yB |
1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
А |
C |
|||||||
ACD = |
|
xC |
yC |
1 |
, |
BCD = |
xC |
yC |
1 |
. |
|
Рис. 7 |
|
|
xD |
yD |
1 |
|
|
x D |
yD |
1 |
|
|
|
Тогда, из точечного исчисления, имеем: |
|
|
|
|
|
|
E |
|||||||||||||||
(А - К)/(B - K) = |
ACD/ |
BCD K = |
B ACD |
− A BCD |
. |
|
K |
|||||||||||||||
|
|
C |
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ACD |
− |
BCD |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|||
Аналогично определим точку К пересечения пря- |
|
|
|
|||||||||||||||||||
мой DE и плоскости АВС (рис. 8): |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
DK/EK = |
DABC/ |
EABC, |
|
|
|
|
|
|
|
|
|
|
|
B |
||||||||
где K = |
E |
DABC −D |
EABC |
. |
|
|
|
|
|
|
|
|
|
D |
||||||||
|
DABC − |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
EABC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 8 |
|||
Определители четвертого порядка составленные из ко- |
|
|
|
|||||||||||||||||||
ординат имеют вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x E |
yE |
zE |
1 |
|
|
|
|
x D |
yD |
z D |
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||||||||||
EABC = |
xA |
yA |
zA |
1 |
|
, |
DABC = |
x A |
yA |
zA |
1 |
|
. |
|
|
|
|
|||||
xB |
yB |
zB |
1 |
|
x B |
yB |
zB |
1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
xC |
yC |
zC |
1 |
|
|
|
|
xC |
yC |
zC |
1 |
|
|
|
|
|
|
||||
Вычисление определителей четвертого порядка
следует проводить спрособом преобразования или разложения по координатам точек
D и Е.
Лекция № 6Б
1.Метрический оператор трех точек. Длина отрезка прямой. Угол между прямыми.
2.Основание перпендикуляра, опущенного из точки на прямую.
3.Точка выхода из плоскости и ее геометрическая интерпретация. Точка выхода из плоскости на расстояние d.
4.Площадь треугольника, расположенного в плоскости общего положения.
5.Определение вершины пирамиды по заданному основанию и высоте.
|
|
МЕТРИЧЕСКИЙ ОПЕРАТОР ТРЕХ ТОЧЕК |
|
|
||
|
В точечном исчислении особое место занимает отношение отрезков |
прямой. Не |
||||
менее важную роль играет произведение этих отрезков. Способ координатного опре- |
||||||
деления произведения отрезков задает метрику пространства, которая характеризует |
||||||
свойства измерений в этом пространстве. |
|
|
|
|||
Определение: Метрическим оператором точек В,С при точке |
C |
|
||||
А называется число, равное произведению длин |
|
|||||
|
|
|||||
направленных отрезков АН и АВ, где Н - ортогональная |
|
|
||||
проекция точки С на прямую АВ: |
|
|
|
|
||
|
|
ΣA = AH × AB |
αBC |
|
|
|
|
|
BC |
|
|
|
|
|
|
|
|
A |
|
B |
Для Евклидового пространства метрический оператор |
|
H |
||||
|
|
|||||
через |
декартовые |
координаты |
заданных |
точек |
Рис. 1 |
|
выражается соотношением: |
|
|
||||
|
|
|
|
|||
|
|
ΣABC = Σ(B−A)(C−A) = |
|
|
|
|
|
= (xB - xA)(xC - xA) + (yB - yA)(yC - yA) + +(zB – zA)(zC - zA). |
|
|
|||
|
Из определения метрического оператора следует, что он не меняется при пере- |
|||||
становке нижних точек-индексов в обозначении: |
ΣABC = ΣCBA . |
|
|
|||
|
|
|
|
|
|
|
Проекции Н соответствует множество точек С перпендикулярное прямой АВ, следовательно, для каждой точки этого множества метрический оператор не меняется. Пусть Н ≡ В, тогда
ΣCBA = AB2
B частном случае, когда С ≡ В, получим квадрат длины отрезка. УТВЕРЖДЕНИЕ. Длина отрезка АВ определяется соотношением:
AB = lAB = 
 ΣABB .
ΣABB .
Непосредственно из рисунка (рис. 1), следует:
ΣA |
|
= AH × AB = |
ΣA |
cos α |
BC |
× ΣA cos α |
BC |
= |
ΣABC . |
|
||||
BC |
|
|
CC |
|
BB |
|
|
|
ΣA |
ΣA |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
BB |
CC |
|
ОСНОВАНИЕ ПЕРПЕНДИКУЛЯРА ОПУЩЕННОГО ИЗ ТОЧКИ НА ПРЯМУЮ |
||||||||||||||
Через метрические операторы определим точку Н (рис. 1). Из геометрического |
||||||||||||||
смысла метрических операторов следует: |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
ΣCAB |
= HB × AB, |
|
|
||||
|
|
|
|
|
|
|
ΣABC = AH × AB. |
|
|
|||||
Разделив второе равенство на первое, получим: |
|
|
|
ΣA |
|
|
||||||||
|
|
|
|
|
|
|
|
AH |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
BC |
|
|
|
|
|
|
|
|
|
|
HB = ΣB . |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
CA |
|
|
Далее, применяя точечное исчисление, получим: |
|
|
|
|
|
|
|
|||||||
|
|
AH |
ΣA |
A−H |
ΣA |
|
AΣB |
+BΣA |
|
|
||||
|
|
|
|
BC |
|
|
BC |
|
|
|
CA |
BC |
|
|
|
|
HB = ΣB H−B |
= ΣB H = |
|
ΣA |
+ΣB |
. |
|
||||||
|
|
|
|
CA |
|
|
CA |
|
|
|
BC |
CA |
|
|
ТОЧКА ВЫХОДА ИЗ ПЛОСКОСТИ И ЕЕ ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ. |
|
|||||||||||||
|
|
ТОЧКА ВЫХОДА ИЗ ПЛОСКОСТИ НА РАССТОЯНИЕ d. |
|
|||||||||||
Для построений над плоскостью общего положения АВС введем понятие точки |
||||||||||||||
выхода из плоскости на заданное расстояние d. |
|
|
|
|
|
|
|
|||||||
ОПРЕДЕЛЕНИЕ. Точкой выхода из плоскости, |
|
|
|
|
K |
|
|
|||||||
|
|
|
|
|
|
|
||||||||
заданной треугольником АВС, называется |
|
|
|
|
|
|
|
|||||||
точка S(syz, szx, sxy) – координатами которой |
|
D |
|
|
C |
|
||||||||
являются |
действительные |
числа |
|
равные |
|
|
|
|
d |
|
|
|||
удвоенным |
|
площадям |
проекций |
этого |
|
|
|
|
|
|
|
|||
ориентированного треугольника. |
|
|
|
d |
|
|
S |
|
|
|||||
Точка S обладает следующими свойствами: |
|
|
|
|
|
|||||||||
|
|
|
|
A |
|
|
||||||||
1. Длина отрезка OS численно равна |
|
|
|
|
|
|
||||||||
площади треугольника АВС. |
|
|
|
|
|
|
|
s |
|
|
|
|||
2. |
|
Прямая |
OS |
перпендикулярна |
|
|
|
|
|
|
|
|||
плоскости треугольника АВС. |
|
|
|
|
|
|
|
Рис. 2 |
B |
|||||
Такими же свойствами обладает векторное |
|
|
|
|
O |
|
||||||||
|
|
|
|
|
|
|||||||||
произведение двух векторов, образованных направленными отрезками сторон ориен- |
||||||||||||||
тированного треугольника АВС. Следовательно, точка выхода является точечным ана- |
||||||||||||||
логом векторного произведения векторов. Через координаты вершин точка выхода из плоскости треугольника АВС определяется соотношениями:
sABCYZ = |
yA |
zA |
1 |
|
sABCZX = |
zA |
xA |
1 |
|
sABCXY = |
xA |
yA |
1 |
|
yB |
zB |
1 |
; |
zB |
xB |
1 |
; |
xB |
yB |
1 |
. |
|||
|
yC |
zC |
1 |
|
|
zC |
xC |
1 |
|
|
xC |
yC |
1 |
|
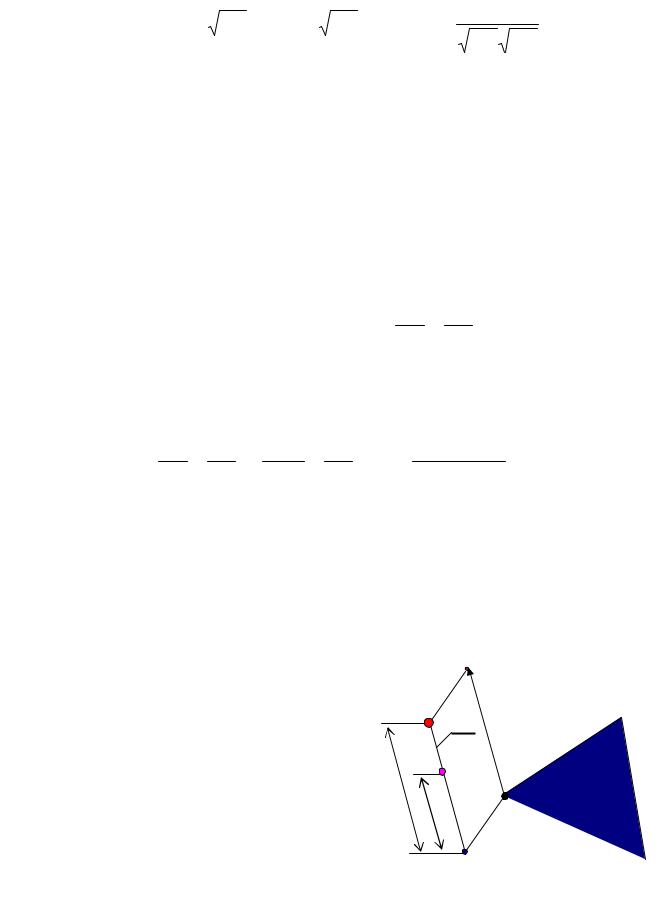
Точка D расположенная на прямой OS, для которой отрезок OD по длине равен числу d, получила название точки выхода из плоскости АВС на величину d:
D = Sd ,
sABC
где sABC – удвоенная площадь треугольника АВС.
Точка D успешно используется для построений над плоскостью общего положения. Точка К (рис. 2), возвышающаяся над точкой А на высоту d, определяется из параллелограмма OAKD суммой точек:
K = A + D
ПЛОЩАДЬ ТРЕУГОЛЬНИКА РАСПОЛОЖЕННОГО В ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ АВС
Для определения точки D необходимо иметь удвоенную площадь треугольника АВС. Поскольку длина отрезка OS, по определению, равна этой удвоенной площади, то через метрический оператор получим:
4s2ABC = ΣSOO = ΣS2 = (syzABC )2 + (szxABC )2 + (sxyABC )2.
Извлекая корень квадратный, находим искомую удвоенную площадь.
ОПРЕДЕЛЕНИЕ ВЕРШИНЫ ПИРАМИДЫ ПО ЗАДАННОМУ ОСНОВАНИЮ АВС И ВЫСОТЕ d
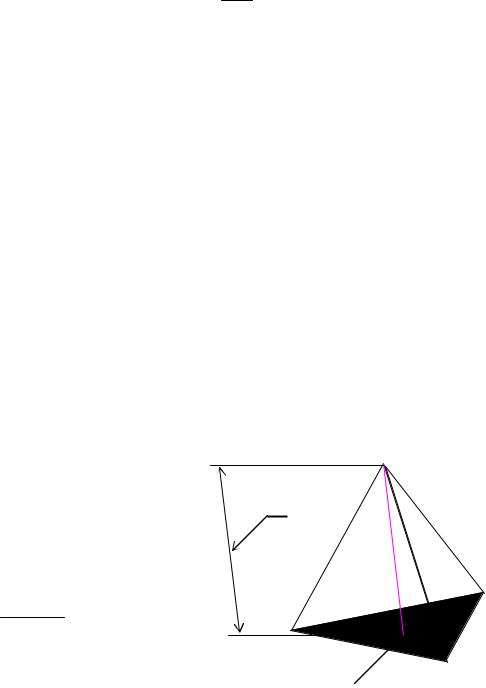
Рассмотрим практическую задачу конструирования пирамиды АВСК, по заданному основанию АВС и высоте d, которая проецируется в центр тяжести основания.
Конструирование пирамиды сводится к определению вершины К.
1.Определим центр Т тяжести треугольника АВС:
T = A+B+C . 3
K
d
C
А
Рис. 3 |
Т |
В |
