
Методичка по МНК-2007
.pdf
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению лабораторной работы на тему «Метод наименьших квадратов» по модулю «Методы решения систем линейных алгебраических уравнений и методы обработки данных в табличном процессоре MS Excel»
по курсу «Информатика» (для студентов строительных и природоохранных
специальностей дневной формы обучения)
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ДОНБАССКАЯ НАЦИОНАЛЬНАЯ АКАДЕМИЯ
СТРОИТЕЛЬСТВА И АРХИТЕКТУРЫ
Кафедра высшей и прикладной математики и информатики
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению лабораторной работы на тему
«Метод наименьших квадратов» по модулю
«Методы решения систем линейных алгебраических уравнений и методы обработки данных в табличном процессоре MS Excel»
по курсу «Информатика»
(для студентов строительных и природоохранных специальностей дневной формы обучения)
УТВЕРЖДЕНО на заседании кафедры
высшей и прикладной математики и информатики Протокол № 2 от 06 . 02 .2007 г.
Макеевка 2007 г.
УДК 517.9: 681.3 (075)
Методические указания к выполнению лабораторной работы на тему«Метод наименьших квадратов» по модулю «Методы решения систем линейных алгеб-
раических уравнений и методы обработки данных в табличном процессореMS Excel» по курсу «Информатика» (для студентов строительных и природоохран-
ных специальностей дневной формы обучения) / Сост. Грицук Ю.В., Митра-
ков В.А., Позднякович А.Е., Акулов В.Ф. – Макеевка, ДонНАСА, 2007. – 16 с.
Методические указания содержат задания к выполнению лабораторной ра-
боты на тему «Метод наименьших квадратов» в рамках модуля «Методы реше-
ния систем линейных алгебраических уравнений и методы обработки данных в табличном процессоре MS Excel» курса «Информатика». Приведены краткие теоретические сведения, индивидуальные задания, примеры выполнения работ и список дополнительной литературы, которая позволяет самостоятельно рас-
смотреть ключевые моменты данного раздела курса «Информатика».
Методические указания ориентированы на формирование предметной мо-
дели специалиста, а именно направлены на развитие операционной деятельно-
сти студента.
Для студентов строительных и природоохранных специальностей дневной формы обучения Донбасской национальной академии строительства и архитектуры.
Составители: |
Ю.В. Грицук, к.т.н., доцент |
|
В.А. Митраков, к.ф-м.н., доцент |
|
А.Е. Позднякович, к.ф-м.н., доцент |
|
В.Ф. Акулов, ассистент |
Рецензент: |
В.А. Моисеенко, к.ф-м.н., доцент |
|
И.Г. Гевлич, к.т.н., доцент |
Ответственный за выпуск |
В.М. Левин, д.т.н., профессор |
СОДЕРЖАНИЕ |
|
Краткие теоретические сведения ............................................................................ |
4 |
Постановка задачи .................................................................................................................... |
4 |
Метод наименьших квадратов ................................................................................................. |
4 |
Линейная аппроксимация ........................................................................................................ |
5 |
Квадратичная аппроксимация .................................................................................................. |
6 |
Варианты индивидуальных заданий ..................................................................... |
12 |
Литература.............................................................................................................. |
15 |
3
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
ПОСТАНОВКА ЗАДАЧИ
Определение вида функциональных зависимостей, получаемых в физическом эксперименте, имеет очень важное значение. Так, в результате экспери-
ментов часто получают совокупность точек(x1 , y1 )...(xN , yN ), абсциссы {xk }
которых различны. Одно из назначений методов обработки экспериментальных данных – определение формулы вида y = f ( x ) , которая связывает эти пере-
менные, точнее – выбор класса допустимых формул, коэффициенты в которых должны быть определены.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Пусть зависимость между переменными x и y представлена таблицей данных, полученных в эксперименте:
|
X |
x1 |
x2 |
|
… |
xN |
|
|
|
|
|
|
|
|
|
|
Y |
y1 |
y2 |
|
… |
yN |
|
|
|
|
|
|
|
|
|
|
Требуется полученные данные описать некоторой функциональной зави- |
||||||
симостью вида y = f ( x ). Такая зависимость |
должна отразить основную тен- |
||||||
денцию изменения переменной y с изменением переменной x и сгладить слу-
чайные погрешности измерений, которые неизбежны в эксперименте.
Задача нахождения эмпирической формулы (формулы, служащей для аналитического представления опытных данных) состоит из двух основных этапов.
На первом этапе необходимо установить вид зависимостиy = f ( x ), т.е.
решить |
является |
|
ли |
она |
линейнойf (x ) = a0 + a1 × x , |
квадратичной |
|||||
f (x )=a +a |
1 |
× x+a |
2 |
× x2 |
, |
логарифмической |
f (x )=a +a |
1 |
× ln(x ) |
или какой-либо |
|
0 |
|
|
|
|
|
0 |
|
|
|||
иной. Для этого экспериментальные точки наносятся на координатную плоскость и по их расположению выдвигают гипотезу о виде эмпирической зависимости.
На втором этапе, когда общий вид эмпирической функции выбран, необходимо определить числовые значения ее параметровa0 , a1 , a2 ,..., an . Для оп-
ределения значений параметров применяетсяметод наименьших квадратов
(МНК).
В методе наименьших квадратов аппроксимирующая функция строится на основании того, что сумма квадратов невязок по всем точкам должна быть
4
наименьшей. Т.е.: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
2 |
N |
|
|
|
|
|
|
2 |
|
|
|
F = |
å |
d |
k |
å( |
f |
( |
x |
k |
) |
k ) |
Þ min , |
|
||
|
= |
|
(1) |
||||||||||||
|
|
|
|
|
|
- y |
|
|
|||||||
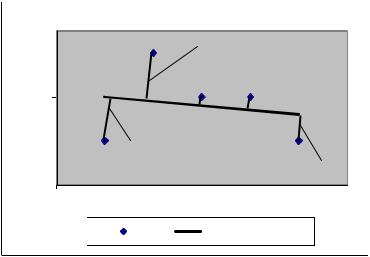
где dk |
– невязки (рис. 1). |
k=1 |
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3,5 |
|
|
|
|
|
|
Yi |
|
d2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,5 |
|
|
|
|
d1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
dk |
||
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
Yi |
|
|
|
|
Линейная (Yi) |
|
|||
Рис. 1. Набор исходных точек, линейная аппроксимирующая функция и невязки для метода наименьших квадратов
Если в качестве f (x ) взять полином (полиноминальная аппроксимация)
в виде:
f (x )=a +a |
1 |
× x+a |
2 |
× x2 |
+...+a |
m |
× xm |
, |
(2) |
0 |
|
|
|
|
|
|
то получаем функцию F = F (a0 ,a1 ,...,am ), зависящую от искомых пара-
метров a0 ,a1 , ...,am .
Заметим, что степень полинома m должна быть меньше числа точекN . (В случае m = N - 1 получим полином Лагранжа).
ЛИНЕЙНАЯ АППРОКСИМАЦИЯ
В этом случае m = 1 , тогда аппроксимирующая функция будет иметь вид:
f (x )=a0 +a1 × x |
(3) |
Согласно МНК значения ее параметров подбираются таким образом, что- |
|
бы отклонение экспериментальных точек (xk ; yk ) |
от выбранной прямой было |
минимальным. Т.е. параметры a0 , a1 должны быть такими, чтобы сумма квад-
ратов отклонений наблюдаемых значений yk от рассчитанных по функции(3),
была минимальной. Сумма квадратов отклонений от линейной функции(3) имеет вид:
5
N |
|
F (a0 , a1 ) = å(a0 + a1 × xk - yk )2 Þ min |
(4) |
k =1
Величина F (ao ,a1 ) есть функция двух переменных. Необходимым усло-
вием экстремума такой функции является равенство нулю всех ее частных про-
изводных: |
|
|
|
|
|
|
|
|
¶F (ao |
,a1 ) |
= 0 |
¶F (ao |
,a1 ) |
= 0 |
(5) |
|
¶a0 |
|
¶a1 |
||||
|
|
|
|
|
|||
Они имеют вид:
ì |
¶F (a0 , a1 ) |
N |
|
ï |
= 2å(a0 + a1 × xk |
||
¶a0 |
|||
ï |
k =1 |
||
í |
¶F (a0 , a1 ) |
N |
|
ï |
|||
ï |
|
= 2å(a0 + a1 × xk |
|
¶a1 |
|||
î |
k =1 |
- yk ) = 0
(6)
- yk )× xk = 0
Таким образом, после преобразования имеем нормальную систему двух линейных уравнений относительно неизвестных параметров регрессии a0 , a1 .
|
|
|
|
|
ì |
|
N |
N |
|
|
|
|
|
|
|
|
|
|
|
å xk = å yk |
|
|
|||||
|
|
|
|
|
ïa0 × N + a1 × |
|
|
||||||
|
|
|
|
|
ï |
|
k =1 |
k =1 |
|
|
|
(7) |
|
|
|
|
|
|
í |
N |
|
N |
N |
|
|||
|
|
|
|
|
ïïa0 × å xk + a1 × åxk2 = å yk × xk |
||||||||
|
|
|
|
|
î |
k =1 |
= |
k 1 = |
k |
1 |
|
|
|
Решение системы – |
значение параметров a0 , |
a1 можно найти, например, |
|||||||||||
методом обратной |
матрицы или |
методом |
Гаусса. Представим систему (7) в |
||||||||||
матричной форме: |
|
|
|
|
|
|
|
|
|
|
|
||
é |
|
N |
ù |
|
|
|
é N |
ù |
|
|
|
|
|
ê |
N |
åxk ú |
éa |
ù |
êå yk |
ú |
|
éa |
ù |
= B |
|||
ê |
N |
k =1 |
ú |
× ê |
0 |
ú |
= êk =1 |
ú |
или A × ê |
0 |
ú |
||
ê |
N |
ú |
ë |
a |
û |
ê N |
ú |
|
ë |
a |
û |
|
|
ê |
åxk |
åxk2 |
ú |
1 |
êå yk × xk ú |
|
1 |
|
|||||
ëk =1 |
k 1 |
û = |
|
ëk 1 |
=û |
|
|
|
|
|
|||
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
éa |
ù |
|
|
|
|
(8) |
|
|
|
|
|
|
|
ê 0 |
ú = A-1 × B |
|
|
|
||
|
|
|
|
|
|
|
ëa1 û |
|
|
|
|
|
|
Найденные параметры a0 , a1 подставляют в уравнение (3) и таким образом получают эмпирическое линейное уравнение наилучшим образом описывающее экспериментальные данные.
КВАДРАТИЧНАЯ АППРОКСИМАЦИЯ
При m = 2 получаем функцию:
6
f(x ) = a0 + a1 × x + a2 × x2
Вэтом случае нормальная система имеет вид:
ì¶F (a , a ,a |
2 |
) |
N |
||||
ï |
0 |
|
1 |
|
|
= 2å(a0 + a1 × xk + a2 × xk 2 - yk ) = 0 |
|
¶a0 |
|
|
|
|
|||
ï |
|
|
|
|
k =1 |
||
ï |
¶F (a , a |
|
,a |
|
) |
N |
|
ï |
1 |
2 |
= 2å(a0 + a1 × xk + a2 × xk 2 - yk )× xk = 0 |
||||
í |
0 |
|
|
|
|||
¶a1 |
|
|
|
|
|||
ï |
|
|
|
) |
k =1 |
||
ï |
¶F (a , a |
1 |
,a |
2 |
N |
||
ï |
0 |
|
|
|
= 2å(a0 + a1 × xk + a2 × xk 2 - yk )× xk 2 = 0 |
||
¶a |
|
|
|
|
|
||
ï |
2 |
|
|
|
|
k =1 |
|
î |
|
|
|
|
|
|
|
(9)
(10)
После преобразования имеем нормальную систему трех уравнений отно-
сительно неизвестных параметров регрессии a0 , a1 , a2 .
ì |
|
N |
|
N |
N |
|
× N + a1 × åxk + a2 × |
åxk2 = å yk |
|
||||
ïa0 |
|
|||||
ï |
|
k =1 |
= |
k 1 = |
k 1 |
|
|
|
|
|
|
|
|
ï |
N |
N |
|
N |
N |
|
ía0 × å xk + a1 × åxk2 + a2 × åxk3 = å xk × yk |
(11) |
|||||
ï |
k =1 |
= k 1 |
= |
k 1= |
k 1 |
|
ï |
N |
N |
|
N |
N |
|
ïa0 × å xk2 + a1 × åxk3 + a2 × å xk4 = å xk2 × yk |
|
|||||
î |
k =1 |
= k 1 |
= |
k 1= |
k 1 |
|
Решив систему (11) |
относительно |
параметров a0 , a1 , a2 |
получаем кон- |
|||
кретный вид функции (9). Изменение количества параметров не приведет к изменению сути самого подхода, а выразится в изменении количества уравнений
в системе (11). |
|
Значения разностей |
|
yk - F (a0 ,a1 ,a2 ) = ek |
(12) |
называют отклонениями измеренных значений от вычисленных по формулам
(3) или (9).
Сумма квадратов отклонений
N |
|
s = åek2 |
(13) |
k=1
всоответствии с принципом наименьших квадратов для заданного вида при-
ближающей функции должна быть наименьшей.
Из двух разных приближений одной и той же табличной функции лучшим считается то, для которого (13) имеет наименьшее значение.
Аналогично можно записать систему для полинома любой степени m £ N :
f (x ) = a |
+ a × x + a |
2 |
× x2 |
+ ... + a |
m |
× xm |
(14) |
0 |
1 |
|
|
|
|
При этом, если m = N , то точечная средняя квадратичная аппроксимация алгебраическим многочленом совпадает с лагранжевой интерполяцией. Другой
7

путь повышения качества аппроксимации связан с выбором вместо алгебраических полиномов других ортогональных полиномов, а также функций вида:
y = a × xb |
y = a × bx |
y = a + |
b |
|
|||
x |
|||||||
|
|
|
|
|
|||
1 |
|
x |
(15) |
||||
|
|
|
|
||||
y = |
|
y = |
|
y = a × lg x |
|||
a × x + b |
a × x + b |
||||||
и других, которые легко линеаризуются путем логарифмирования или замены переменных (табл. 1, рис. 2).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 |
||||
|
|
|
Замена переменной (переменных) для метода линеаризации данных |
||||||||||||||||||||||||||||||||||
Функция, y = f ( x ) |
|
Линеаризованная форма, |
Замена переменной |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y = A × x + B |
|
|
|
(переменных) и |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
постоянных |
|||||||||||
y = |
|
A |
+ B |
|
|
|
|
y = A × |
1 |
|
+ B |
|
X = |
1 |
, Y = y |
|
|
|
|
|
|||||||||||||||||
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y = |
|
|
D |
|
|
|
|
y = |
-1 |
× (x × y) + |
D |
|
|
X = x × y , Y = y , |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
-D |
|
|
|
|||||||||||||||||
|
|
x |
+ C |
|
|
|
|
|
|
|
C |
|
|
|
|
C |
|
A = |
, B = |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
C |
|
|
|
|
|
y = |
|
|
1 |
|
|
|
|
|
1 |
= A × x + B |
|
X = x , Y = |
1 |
|
|
|
|
|
|
|
|||||||||||||||||
|
A |
× x + B |
|
|
|
y |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
y = |
|
|
x |
|
|
|
|
1 |
= A × |
1 |
+ B |
|
X = |
1 |
, Y = |
1 |
|
|
|
|
|
|
|||||||||||||||
|
A |
× x + B |
|
|
|
|
x |
y |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
y |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
y = A × ln( x) + B |
|
y = A × ln( x) + B |
|
X = ln( x ), Y = y |
|
||||||||||||||||||||||||||||||||
y = C × e A×x |
|
|
|
ln( y) = A × x + ln(C ) |
|
X = x , Y = ln( y) , |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = ln(C ) |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
y = C × x A |
|
|
|
ln( y) = A × ln(x ) + ln(C ) |
|
X = ln( x ), Y = ln( y) , |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = ln(C ) |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
y = (A × x + B)-2 |
|
y-1 2 = A × x + B |
|
X = x , Y = y-1 2 |
|
|
|
|
|||||||||||||||||||||||||||||
y = C × x × e- D×x |
|
|
æ y ö |
= -D × x + ln(C ) |
|
X = x |
|
|
|
|
|
|
æ y ö |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
lnç |
|
÷ |
|
, Y = lnç |
|
|
|
÷ , |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
è |
x ø |
|
|
|
|
|
|
|
|
|
|
è |
|
|
ø |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = -D , B = ln(C ) |
||||||||||||||
|
|
|
L |
|
|
|
æ |
L |
|
|
ö |
|
|
|
|
|
|
æ |
L |
|
ö |
||||||||||||||||
y = |
|
|
|
|
lnç |
- 1÷= A × x + ln(C |
) |
X = x |
, Y = lnç |
|
- 1÷ , |
||||||||||||||||||||||||||
1 + C × e |
A×x |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
y |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
è |
|
y |
ø |
|
|
|
|
|
|
è |
|
|
ø |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = ln(C ) и L – посто- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
янные, которые должны |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
задаваться |
|
|
|
|
|
|||||||||
8
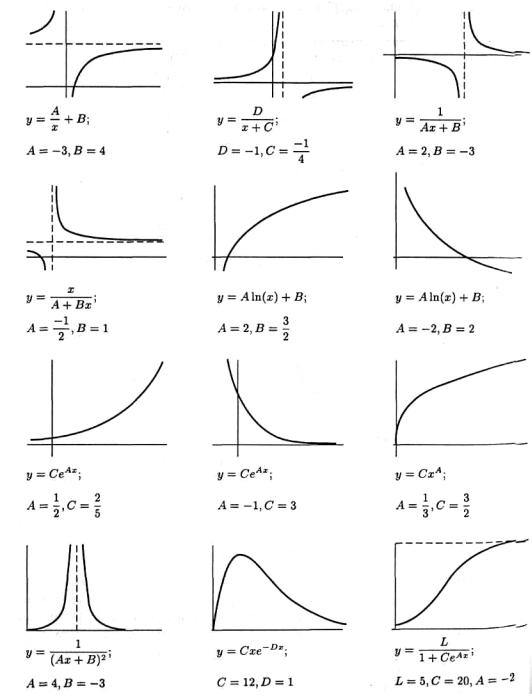
Рис. 2. Возможные кривые, которые используются в методе линеаризации данных
Пример реализации метода наименьших квадратов в средеMicrosoft Excel представлен на рис. 3 и 4.
9
