Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донбасская национальная академия строительства и архитектуры

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

sopromat 2course

.pdf

Скачиваний:

Добавлен:

21.02.2016

Размер:

2.42 Mб

Скачать

☆

1 / 51 2 3 4 5 > Следующая >>>

МОДУЛЬ 1. Задачі курсу "Основи теорії споруд". Короткий історичний огляд. Основні геометричні характеристики плоских перерізів. Сортамент прокатних профілів.

1.1. ВВЕДЕНИЕ. РОЛЬ КУРСА В РАБОТЕ АРХИТЕКТОРА

Окружающий нас мир наполнен творениями рук и ума человека. Это машины, самолеты, корабли, высотные здания, мосты, плотины, нефтепроводы и т. д. Все это принято называть конструкциями. Основной задачей архитекторов и строителей в процессах проектирования и строительства зданий и сооружений является обеспечения прочности и долговечности конструкций. Известно много памятников архитектуры, которые пережили тысячелетие и сохранили достаточную прочность. Давнишние строители старались придать своим сооружениям большие запасы прочности, устраивая их слишком толстыми стенами, массивными колонами. К сожалению, сохранилось немного сведений о том, как определялись размеры элементов сооружений. Древние сооружения не отличались конструктивным разнообразием: строители копировали старые, проверенные временем конструктивные формы. Конструктивные изменения закреплялись в строительной практике очень медленно. При современном развитии техники и большому разнообразию типов сооружений уже нельзя в строительстве полагаться на время: сейчас необходимо строить быстро, прочно и экономично.

При проектировании конструкций необходимо определить внешние нагрузки, которые будут действовать на них, выяснить законы изменения внутренних усилий в разных частях конструкции, и подобрать размеры элементов этой конструкции так, чтобы все они были крепкие и не имели слишком больших запасов несущей способности.

Равновесие и движение сооружений или их элементов и методы их расчетов на прочность, жесткость и устойчивость изучает наука “Теория сооружений”.

Равновесие тела – это состояние относительного покоя или состояние, при котором все точки тела перемещаются равномерно и прямолинейно.

Абсолютно твердое тело – это такое тело, у которого расстояния между всеми его точками при любом механическом воздействии остаются неизменными.

Курс “Основы теории сооружений” состоит из нескольких дисциплин:

а) теоретической механики, б) сопротивления материалов, в) строительной механики.

Объектами изучения этих дисциплин в рамках настоящего курса являются абсолютно твердое тело (1.2), стержень (6.1), стержневые конструкции (6.2).

Все перечисленные дисциплины не задевают вопроса о внутреннем строении тела, но базируются на экспериментально проверенных предположениях (гипотезах), что учитывают их физические свойства.

Теоретическая механика изучает равновесие и движение твердого тела; состоит из трех частей: статики, кинематики, динамики. Сопротивление материалов и строительная механика изучают методы расчетов на прочность, жесткость и устойчивость соответствующих конструкций.

1.2. КРАТКИЙ ИСТОРИЧЕСКИЙ ОЧЕРК

Наука о поведении материалов под нагрузкой, очевидно, возникла тогда, когда у человека появилась потребность в создании сложных сооружений, постройке больших морских судов. Точно назвать такую дату нельзя. Первые сооружения - египетские пирамиды Хеопса высотой 145 метров были построены 1000 лет до новой эры. Мы не перестаем удивляться мастерству древних строителей, воздвигших прекрасные акведуки в Древнем Риме, дворцы в Византии, храмы в Древней Руси, культовые сооружения Востока.

К сожалению, до наших дней дошли только те сооружения, в которых строители удачно и без ошибок скопировали природу. Как правило, в таких сооружениях действовали

только сжимающие напряжения. И если в сооружения прокрадывались растягивающие деформации, то, вероятно, последствия были печальны.

Первым ученым, применившем расчет в кораблестроении, был Леонардо да Винчи (1452-1519). Галилео Галилей (1564-1642) – второй крупный ученый эпохи Возрождения. Г. Галилей исследовал растяжение и изгиб стержней. Испытывая на растяжение стержни, он установил, что сила, разрывающая стержень, пропорциональна его площади поперечного сечения. Таким образом, для простейшего случая нагружения — растяжения стержня Галилей неявно определил понятие напряжения в момент разрыва. Он впервые поставил задачу об определении разрушающей силы для консольной балки прямоугольного поперечного сечения, нагруженной силой на свободном конце. Работы Г. Галилея положили начало становлению науки о прочности материалов.

В1660 году Роберт Гук (1635-1703) пришел к выводу о существовании пропорциональной зависимости между напряжениями и деформациями. Проверял этот закон он 18 лет.

Еще в XIX веке инженеры практики делали расчеты, как говорят, на пальцах. При пропорциональном увеличении размеров парусного судна оно разрушалось. Несколько позже частыми стали аварии пароходов. В Англии с 1882 по 1885 год потерпели аварию 228 пароходов. В США за 12 лет с 1876 года обрушился 251 мост. Эти и многие другие примеры убедили инженеров в пользе обоснованных расчетов. При этом обнаружилось, что правильный расчет может и удешевить конструкцию, так как позволяет экономить материал.

Важный вклад в науку о прочности материалов сделал в середине XVIII века петербургский академик Леонард Эйлер (1707-1783), написавший в общей сложности более 800 работ по различным теоретическим и прикладным проблемам.

Вконце XVIII века французский ученый Кулон (1736 -1806) разработал важную в то время теорию сводов. Будучи прекрасным экспериментатором, он решил некоторые задачи в области кручения.

Всему миру известны труды выдающихся ученых, Тимошенко С.П., Власова В.З. Крылова А.Н. решивших сложные и актуальные задачи в области строительства и других областях. Изучением поведения элементов конструкций в экстремальных условиях занимался наш украинский соотечественник Писаренко Г.С.

3.2.ОСНОВНЫЕ ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ

ИПРИМЕРЫ ИХ ВЫЧИСЛЕНИЙ

Врасчетах на прочность (3.1), жесткость (3.2) и устойчивость (3.3) используются геометрические характеристики площади поперечного сечения стержней. Например, при растяжении стержня используется простейшая геометрическая характеристика – площадь поперечного сечения. В других случаях напряженно-деформированного состояния потребуются другие, более сложные геометрические характеристики, которые целесообразно изучить заранее, прежде чем приступить к непосредственному изучению расчетов на прочность и жесткость.

Восновных простейших видах напряженно-деформированного состояния стержня используются следующие геометрические характеристики поперечного сечения: статические моменты площади Sx, Sy; осевые моменты инерции площади Ix, Iy; центробежный момент

инерции площади Ixy; полярный момент инерции площади I .

Рассмотрим некоторое произвольное поперечное сечение стержня (рис. 3.2), помещенного в систему координат (x, y). Выделим в сечении элемент бесконечно малой площади dF 0. Положение такой площадки будет характеризоваться координатами (x, y). Расстояние от центра координат до площадки – полярный радиус, обозначим .

Статическими моментами площади F относительно осей x и y называются величины Sx и Sy , определяющиеся по формуле:

S	x

ydF F

S	y

xdF F

(3.1)

Осевыми моментами инерции площади F относительно осей x и y называются величины Ix и Iy, определяющиеся по формуле:

(3.2)

Центробежным моментом инерции площади F относительно системы осей (x, y) называется величина Ix y, определяющаяся по формуле:

I	xy

xydF F

(3.3)

Полярным моментом инерции определяющаяся по формуле:

площади F называется величина I ,

dF	(3.4)
.

В связи с тем, что в формулах (3.2), (3.4) под интегралом находятся квадраты координат, значения осевых моментов инерции площади и полярные моменты инерции площади всегда будут положительными. Статические моменты инерции (3.10) и центробежный момент инерции площади (3.12) могут иметь любой знак и могут быть равными нулю.

При этом, поскольку

	x	2	y	2
		2		2

, полярный момент инерции площади (3.13) может

быть найден как сумма осевых моментов инерции площади (3.11):
I 2 dF (x y)2 dF I x I y .	(3.5)

Всоответствии с приведенными формулами (3.1)-(3.4) единицами измерения

статических моментов площади являются Sx, Sy [см3], осевых, центробежного и полярного моментов инерции площади - Ix, Iy, Ix y, I [см4].

Помимо приведенных выше основных геометрических характеристик следует познакомиться еще с несколькими производными характеристиками, которые также используются в расчетах на прочность (3.1) и устойчивость (3.3).

Моментами сопротивления площади F относительно осей x и y называются величины Wx и Wy, равные отношению соответствующих моментов инерции Ix, Iy к координатам точек сечения уmax, xmax, максимально удаленных от данной оси:

W		I		x
W

	x	y
		y	max
			max

W		I		y
				y
	y	x
	y
			max
			max

(3.6)

Единицами измерения момента сопротивления площади являются Wx, Wy [см3].

Радиусами инерции площади относительно осей x и y называются величины ix и iy, равные корню квадратному из отношения соответствующих моментов инерции Ix, Iy к площади поперечного сечения F:

I y

(3.7)

Единицами измерения радиусов инерции площади являются ix, iy [см]. Проиллюстрируем вычисление геометрических характеристик на примеры

прямоугольного и круглого сечений.

Пусть в прямоугольном сечении размерами bxh задана система координат (x, y) так, что оси x и y являются осями симметрии данного сечения (рис. 3.3). Выделим в прямоугольнике на некотором расстоянии y от оси x полоску шириной b и высотой dy 0. Тогда площадь такой полоски определится как dF=b dy. В соответствии с (3.1) статический момент площади (3.10) прямоугольника относительно оси x найдем как:

Sx	ydF
	F

	h
	2
	y
	h
	2

y		2	h	2	h		2	h	2
y					h			h
bdy b					b
bdy b					b					0	.
	2					8		8			.
	2			h		8		8
					2
					2

Осевой момент инерции площади (3.11) прямоугольника относительно оси x найдем как:

						h			y			h	h			h		bh
						2			y		3	2	h		3	h	3	bh	3
I			y	2	dF		y	2	bdy b				b
				2				2
	x									3				24		24		12
		F				h				3		h		24		24		12
		F				h						h
						2							2

Рассуждая аналогично нетрудно получить значения статического момента площади и осевого момента инерции площади относительно оси y:

							b				b		2		b	2
							2				b		2		b	2
		y																		;
S				xdF				x hdy h				8			8				0
			F			b						8			8
							2
							b	2				b		3				3			3
								2						3			b	3		hb	3
I	y			x		dF			x								b			hb
I	y			x		dF			x
					2					2
			F				b					24					24			12
								2

Центробежный момент инерции площади (3.12) прямоугольника относительно системы координат (x,y):

	h
I xy xydF	20 y bdF 0 .
F	h
	2

Полярный момент инерции площади (3.13) найдем в соответствии с (3.5):

I I x I y		bh3		hb3		bh	h2	b2 .

	12		12		12

Моменты сопротивления площади (3.14) прямоугольного сечения:

W		I		x
W

	x	y
		y	max
			max
W		I		y
				y
	y	x
	y
			max
			max

bh	3
bh	12	bh
		bh

h		6
h		6
	2
hb	3
hb	12	hb
		hb

b		6
b		6
	2

;

Радиусы инерции площади (3.15) прямоугольного сечения:

bh3

hb3

I y

I x

0.2887h;

0.2887b .

Иногда для получения геометрических характеристик удобно использовать полярную систему координат, как, например, в случае с круглым сечением (рис.3.4). В соответствии с (3.4) Полярный момент инерции площади (3.13) круглого сечения определится как:

				r			4	r	r	4
				r			4		r	4
I			dF
		2			2
	F			0		4		0	2
								0

В соответствии с (3.5) осевые моменты инерции площади (3.11) определятся как:

				I
I		I
I	x	I	y	2
	x		y

r 4

3.3. СОРТАМЕНТ ПРОКАТНЫХ ПРОФИЛЕЙ

Изучение расчетов элементов конструкций будем производить на основе наиболее простого случая материала стержня – металлического стержня. Большинство металлов и сплавов являются изотропными материалами, что существенно облегчает расчет. Наиболее распространенный в строительной практике металл – это сталь. Сталью является сплав железа с углеродом. Доля углерода в стали и процентное содержание различных химических соединений и элементов, обуславливают наличие сталей разных марок по своим характеристикам. Для изготовления стержневых элементов применяются прокатные профиля, т.е. профиля полученные в заводских условиях способом прокатки. Основными прокатными профилями, применяющимися в строительстве, являются: двутавры, швеллера, уголки, листы, трубы, круги и квадраты. Номенклатура сечений этих профилей приведена в соответствующих ГОСТах (ДСТУ) и называется сортаментом.

Сортаментом прокатных профилей называется совокупность профилей по форме их поперечного сечения и размеров, которые изготавливаются в заводских условиях способом прокатки. Современный архитектор обязан знать и различать основные типы прокатных профилей, представленных в табл. 3.1.

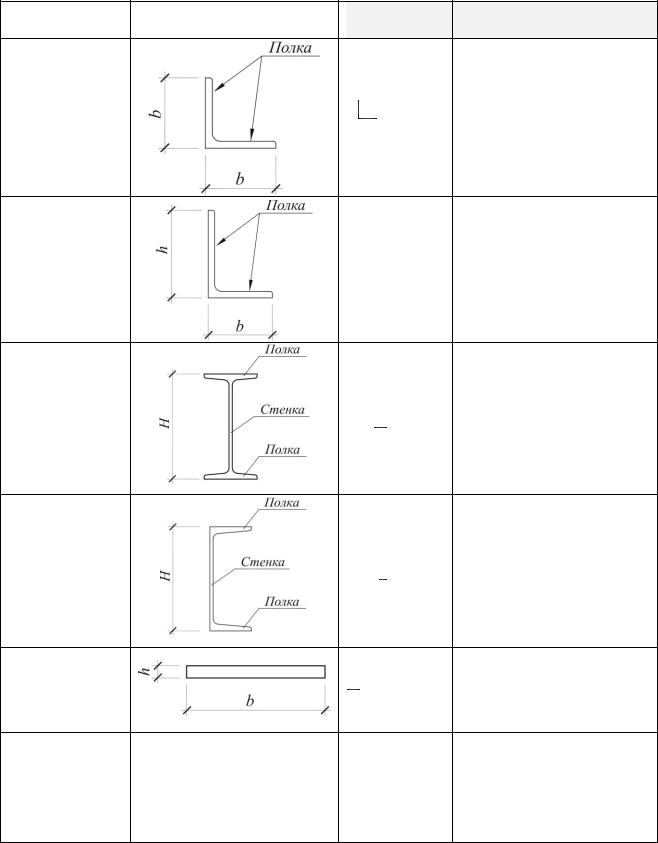
Основные типы прокатных профилей

Наименование	Эскиз	Условное
		Условное
		обозначение
		обозначение

	Уголок	50x5
	равнополочный	50x5
	равнополочный

Таблица 3.1

Описание

Равнополочный (равнобокий) уголок имеет две полки одинакового размера. В условном обозначении указывают ширину полки b и толщину полки в миллиметрах.

Уголок

неравнополочный

Двутавр

Швеллер

Лист

75x50x5

300x15

Неравнополочный (неравнобокий) уголок имеет две полки разных по ширине размеров. В условном обозначении указывают ширину обеих полок h и b и толщину полки в миллиметрах.

Двутавр имеет две оси симметрии и состоит из двух полок, соединенных между собой стенкой. В условном обозначении указывают только номер двутавра по сортаменту, который равен высоте двутавра H в сантиметрах.

Швеллер имеет одну ось симметрии и состоит из двух полок, соединенных между собой стенкой. В условном обозначении указывают только номер швеллера по сортаменту, который равен высоте двутавра H в сантиметрах.

Лист (пластина) сечение прямоугольное, размерами bxh. В условном обозначении указываются оба размера сечения в миллиметрах.

		Круглая	труба		характеризу-
		ется внешним диаметром D и
Труба круглая	Тр. 300х8	толщиной стенки t. В
		условном			обозначении

		указываются оба эти размера
		сечения в миллиметрах.
		Труба		прямоугольная
		характеризуется			размерами
		внешних граней h, b и
		толщиной стенки t. В
Труба		условном			обозначении
		указываются три эти размера
прямоугольная	Тр.80х60х8
		сечения	в	миллиметрах. В
(квадратная)
		случае	квадратной			трубы,

		когда h=b, в условном
		обозначении		также		приводят
		три размера, два из которых
		одинаковы.
		Круглое сечение характеризу-
		ется	только			внешним
Круг	30	диаметром D. В условном
		обозначении			указывают

		внешний		диаметр			в
		миллиметрах.
		Квадратное				сечение
		характеризуется				размером
		грани квадрата b. В условном
Квадрат	20	обозначении		указывают			этот
		размер в миллиметрах.

Тема 2. Зависимость между геометрическими характеристиками при преобразовании системы координат. Понятие центра тяжести и главных осей инерции сечения

4.1. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ОСЕЙ. ПОНЯТИЕ ЦЕНТРА ТЯЖЕСТИ

Геометрические характеристики сложных составных сечений непосредственным интегрированием вычислять затруднительно. Можно разбить составную фигуру на отдельные простейшие, для которых геометрические характеристики уже известны, и интегрирование заменить суммированием. При этом возникает необходимость знать зависимости между геометрическими характеристиками плоских сечений при параллельном переносе и повороте системы координат вокруг ее начала.

Рассмотрим случай параллельного переноса координатных осей. Вычислим статический момент площади (3.10) относительно оси х1, смещенной параллельно на расстояние a от прежней оси x, относительно которой статический момент площади Sx известен:

Sx1 y1dF ( y a)dF ydF a dF Sx aF .

F F F F

При некотором расстоянии между осями ac статический момент площади окажется равным нулю. Положив Sx1=0, найдем

a	c

	S	x


	F

(4.1)

Ось, относительно которой статический момент равен нулю, называется центральной. Пересечение центральных осей определяет точку называемую центром тяжести.

Из (4.1) следует, что при известном положении центра тяжести фигуры, момент площади (3.10) можно вычислить не прибегая к интегрированию, т.е.

где xc, yc – координаты центра тяжести фигуры.

Для составной фигуры:

y F y

x F

i i

c i ,

i i

x F

;

y F

статический

(4.2)

Fi , откуда

(4.3)

Рассмотрим порядок определения центра тяжести (4.2) на примере произвольной фигуры, показанной на рис. 4.2.

1.Фигура разбивается на простейшие, для которых просто определяются площади (F1, F2, F3) и центры тяжести (C1, C2, C3).

2.Вводится некоторая

вспомогательная система координат (произвольно).

3.Определяются координаты центров тяжести каждой простой фигуры в вспомогательной системе координат (xi, yi).

4.Вычисляются координаты

центра тяжести фигуры (xc, yc) по формулам (4.3).

5. По полученным координатам определяется точка центра тяжести на чертеже.

Заметим, что если фигура имеет ось симметрии, то центр тяжести всегда находится на этой оси. Если таких осей две, например прямоугольник, двутавр и пр., то центром тяжести является точка пересечения этих осей. Также следует отметить, что любая ось, проходящая через центр тяжести (4.2) является центральной осью (4.1). Таким образом, количество центральных осей для сечений бесконечно.

В дальнейшем за исходную систему координат будем принимать систему центральных осей (4.1). Пусть в некоторой системе центральных осей Xc, Yc осевые моменты инерции (3.11) известны (рис. 4.3). Требуется вычислить моменты инерции в системе координат, поступательно смещенных на расстояние a и b относительно прежней системы.

Осевые моменты инерции (3.11) определяются по формуле (3.2):

a y

dF a

F 2a

y dF

F 2aS

x .

Поскольку ось xc – центральная, то

. Тогда

(4.4)

Аналогично рассуждая, нетрудно почить остальные зависимости между моментами инерции:

I		I		b	2	F	;
					2
	y		y	c
				c

I	xy	I	x y	c	abF	.
			c	c

(4.5)

Выражения (4.4) и (4.5) представляют собой зависимости между моментами инерции при параллельном переносе системы координат. Следует отметить, что расстояния a и b являются координатами точки начала координат, и, как и любые координаты, могут принимать как положительные, так и отрицательные значения.

Например, определим моменты инерции прямоугольника относительно системы координат, проходящей через его стороны (рис. 4.4).

Как известно из предыдущей темы, моменты инерции прямоугольника относительно центральных осей имеют вид:

		bh	3					hb		3						0 .
			3
I x		12		; I y		c		12			;		I x	y	c
c		12						12					c
c													c
Тогда в соответствии с (4.4) и (4.5) получим
									bh			3				h	2		bh	3	bh	3	bh	3
												3								3		3		3
I x	I x			a	2		F											bh
I x	I x			a			F		12									bh	12		4		3
		c							12							2			12		4		3
		c

	2		hb3	b		2	hb3	hb3	hb3
I y I y	b	F			bh					,
I y I y	b	F	12		bh		12	4	3	,
	c		12	2			12	4	3
	c

abF 0

x y

4.2. ПОВОРОТ КООРДИНАТНЫХ ОСЕЙ

Пусть для некоторой фигуры в системе координат x, y моменты инерции площади Ix, Iy, Ixy известны. Вычислим моменты инерции площади этой фигуры в системе координат x1, y1, повернутой на положительный угол по отношению к исходной системе координат (рис. 4.5). При этом угол будем считать положительным, если поворот системы координат производится против часовой стрелки.

Очевидно, что AOB= CAD= , как углы между взаимно перпендикулярными прямыми. Тогда

y1 CB CA AB AD cos OAsin ,

откуда получим

y1 y cos xsin .

Аналогично для другой координаты

x1 OB CD OAcos ADsin ,

откуда

x1 x cos y sin .

Согласно определению осевой момент инерции (3.11) определится как:

cos

dF sin

dF 2sin cos

xydF

y cos xsin dF

Подставив уже известные интегральные зависимости, получим

cos

sin

sin 2

(4.6)

Аналогично определится значение осевого момента инерции относительно оси y1:

cos

sin

sin 2

(4.7)

Найдем сумму полученных осевых моментов инерции, сложив выражения (4.6) и (4.7):

cos

sin

sin 2 I

cos

sin

sin 2

sin

cos

sin

I .

cos

Очевидно, что как бы ни была повернута система координат x1, y1 по отношению к исходной системе координат x, y сумма осевых моментов инерции не изменяется. Это утверждение также согласуется определением полярного момента инерции площади (3.13), который согласно (3.5) равен сумме осевых моментов инерции площади, т.е.

I	x	I	y	I	x	I	y	I
	1		1

const

(4.8)

Центробежный момент инерции площади (3.12) в системе координат x1, y1

определится как:

I x1 y1

x1 y1dF x cos y sin y cos x sin dF cos sin y2 dF

2 dF cos2 sin 2

xydF cos sin I

cos sin

cos2 sin 2

Откуда получим

I x y

I x I y

sin 2 I xy cos 2 .

(4.9)

Полученные формулы (4.4)-(4.8) в принципе решают поставленную задачу вначале настоящей темы: определить геометрические характеристики относительно любой системы координат, если известны эти характеристики относительно какой-то системы координат. Однако на практике при решении инженерных задач, как правило, нужно знать, как нужно расположить систему координат, чтобы, например, получить максимальный осевой момент инерции площади (3.11) или нулевой центробежный момент инерции площади (3.12). В этом случае используется понятие главных осей инерции.

1 / 51 2 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.02.2016725.5 Кб146Seysmika.doc
#
21.02.2016474.83 Кб15Slovar_arkhitekt_terminov_Drevny_Rim_i_Vizanti.pdf
#
21.02.20161.37 Mб26Slovar_arkhitekt_terminov_Zapadnoy_Evropy.pdf
#
21.02.2016125.44 Кб12Slovar_Dr_Rim_Vizantia.doc
#
21.02.2016970.75 Кб19Slovar_Zapadnaya_Evropa.doc
#
21.02.20162.42 Mб21sopromat 2course.pdf
#
21.02.2016688.86 Кб31Sopromat_spec_kurs_2003.pdf
#
21.02.2016325.75 Кб16Sortament.pdf
#
14.09.20192.12 Mб5Tema_10.doc
#
14.09.20194.04 Mб27Tema_11.doc
#
14.09.20193 Mб24Tema_12.doc