4.10 Расчет крепления второстепенной балки к главной

Крепление балки осуществляем при помощи болтов нормальной точности.

Принимаем диаметр болта равным 20мм, класс прочности 4.6, класс точности С

Величина усилия в соединении определяется как реакция опоры второстепенной балки. При пролете второстепенной балки равном 5м и нагруженной равномерно распределенной нагрузкой величиной q= 59,4 кН/м, реакция опоры составит

Определяем несущую способность одного болта на срез 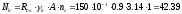кН,

Где

МПа- расчетное сопрот. болта на срез ;

- коэффициент условия работы болтового соединения в расчетах на срез и смятие

=1-количество срезов болтового соединения;

Площадь поперечного сечения одного болта диаметром 20 мм

Несущая способность одного болта на смятие определяем по формуле

Где

=450МПа- расчетное сопротивление болта на смятие

=0,9-коэффициент условия работы болтового соединения в расчетах на срез и смятие;

d=20мм - диаметр болта

= 7,0 мм- наименьшая суммарная толщина элементов, сминаемых в одном направлении ( для нашего случая- толщина стенки второстепенной балки из прокатного двутавра №40Б1)

Определяем расчетное количество болтов болтового соединения:

Для крепления второстепенной балки к главной балке принимаем болтовое соединение на 3 болтах

Конструирование болтового соединения осуществляется согласно требованиям ДБН В.2.6-163:2010

5.Расчет центрально-сжатой сквозной колонны

Требуется Выполнить расчет центрально-сжатой колонны под балочную клетку усложненного типа

размерами в плане – L х l=10.6м х 5 м.

отметка верха настила – Н = 13метров.

Заглубление колонны ниже уровня пола – -0,8 метра.

Примыкание главной балки к колонне – опирание сверху.

Компоновка балочной клетки приведена ниже:

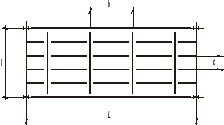
Высота главной балки – 1000 мм;

сечение второстепенных балок – двутавр № 40Б1 (ГОСТ26020-83)

сечение балки настила – двутавр № 14.

Толщина настила балочной клетки t_н = 10 мм.

Примыкание балки настила к второстепенной балке – опирание сверху;

Макс. поперечная сила на опоре главной балки – Q_max = 635,3 кН.

Материал колонн – сталь С245 по ГОСТ 27772-88 с расчетным сопротивлением стали R_y = 240 МПа – для фасонной стали толщиной

4< t ≤20мм.

5.1 Сбор нагрузок на центрально-сжатую колонну и определение расчетных длин колонны:

- геометрическая длина колонны относительно свободной оси ()

- то же, относительно материальной оси ().

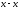Расчетная нагрузка на центрально- сжатую колонну:

=2 635.3=1270.6кН

Определяем расчетные длины колонны по формуле –

где - геометрическая длина колонны;

μ-- коэффициент расчетной длины; при шарнирном закреплении нижнего конца колонны к фундаменту и шарнирном примыкании главной балки к колонне и второстепенной балки к главной балке коэффициент расчетной длины равен –μ=1.

Тогда, расчетные длины колонны:

l_efx = μ·l_x = μ·(H-t_н- h_{б н} –h_{вт б} +h_загл )=1·(13-0,01-0,14-0,392+0,8)=13.258м

l_efу = μ·l_у = μ·(H-t_н- h_гл.б +h_загл )=1·(13-0,01 -1+0,8)=12,79м

Задаемся предварительной гибкостью колонны (средней длины в пределах λ = 90 и находим коэффициент продольного изгиба при материале колонны из стали С235 по ГОСТ 27772-88 с расчетным сопротивлением стали R_y = 230 МПа (для фасонной стали толщиной 4< t ≤ 20мм.

При λ90 и R_y = 230 МПа коэффициент продо4льного изгиба равен φ=0,625 (согласно ДБН В.2.6-163:2010)

Определяем требуемую площадь поперечного сечения ветви колонны:

где = 1

По полученному значению требуемой площади поперечного сечения ветви колонны принимаем его сечение из прокатного двутавра

№ 35Б1 А=49,53;=10060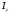=529=14,25см;=3,27см

h = 346мм b = 155мм;

t = 8,5мм; d=6,2мм

Определяем гибкость колонны относительно оси х-

Где φх = 0,591 при =93 иR_y = 240 МПа

Проверяем устойчивость колонны относительно материальной оси х-х:

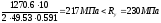
Определяем разнос ветвей из условия равноустойчивости сквозной колонны по формуле

где =0,41 и=0,52.

Принимаем разнос ветвей колонны,округляя в большую сторону b= 36см

Определяем геометрические характеристики сечения относительно свободной оси у-у.:

тогда гибкость сечения-

принимаем расстояние между планками в свету равными =120см.

Тогда гибкость ветви составит

Задаемся размерами планки:

ширина планки – =0,736=25,2см принимаем =26см;

толщина планки -

расстояние между центрами планок -=120+26=146см

собственный момент инерции планки –

Определяем отношение. т. к. 10,1 > 5 =>

гибкость сквозной колонны относительно свободной оси у-у определяется по формуле:

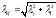
 Составной стержень колонны на планка

Проверяем устойчивость колонны относительно свободной оси у-у:

<230Мпа-устойчивость обеспечена

Где φу =0,693 при =79 иR_y =240Мпа (согласно ДБН В.2.6-163:2010)