3. Графічне розв'язання задачі конструювання піраміди

3.1 План графічних побудов

Для побудови піраміди пропонується такий алгоритм:

1.Знайти точку Т - центр ваги трикутника АВС. Центр ваги трикутника - це точка перетину медіан трикутника ( медіана - це пряма, що з'єднує вершину трикутника з серединою протилежної сторони).

2.Через точку Т провести перпендикуляр до площини трикутника.

3.На перпендикулярі відкласти відрізок заданої довжини, тобто 80мм. Відмітити точку К – шукану вершину піраміди. З'єднати точку К з точками А,В,С.

4.Встановити видимість ребер піраміди за допомогою конкуруючих точок.

3.2. Пояснення до етапів графічного розв'язання задачі

1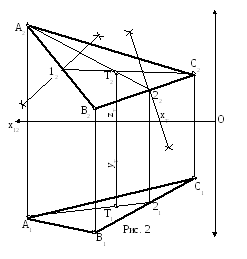.По заданих координатах вершин будуємо проекції трикутникаАВС та знаходимо центр ваги його. Розділяємо сторони АВ та ВС пополам за допомогою циркуля.

Одержані точки 1, 2 з’єднуємо з протилежними вершинами С та А (рис.2).

Точка перетину проведе-них прямих і є центром ваги трикутника - точка Т .

За допомогою вимірів встановлюємо та записуємо координати цієї точки.

Т(x_т,y_т,z_т).

2.Будуємо висоту піраміди.

Висота піраміди – це відрізок прямої, що перпендикулярна до її основи. Тому скористаємося наступними ствердженнями [1]:

-пряма перпендикулярна площині, якщо вона перпендикулярна двом прямим, що перетинаються і належать цій площині;

-в проекціях прямий кут не змінюється тільки з прямими, які паралельні площинам проекцій, тобто з горизонталлю та фронталлю.

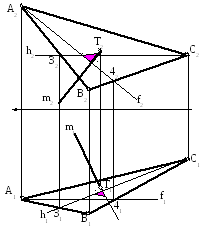
Виходячи з цього, проводимо горизонталь (h_1,h₂) та фронталь (f_1,f₂) трикутника АВС (основи піраміди). Потім з точки Т₂ проводимо пряму m_2, перпендикулярну до f₂, а з точки Т₁ пряму m₁ перпендикулярну до h₁. Два розв'язки цього етапу подані на рис.3(а,б).

Студент креслить один з поданих варіантів.

Рис.3а Рис. 3б

3. Знаходимо шукану вершину піраміди АВСК - точку К

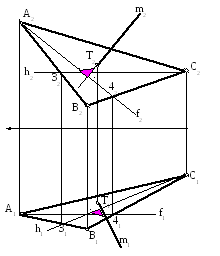
На прямій m візьмемо довільну точку L(L_1,L₂) (рис.4).

Знаходимо дійсну величину відрізка ТL методом прямокутного трикутника (відрізок Т₁L₀). Спочатку на цьому відрізку відкладаємо відрізок завдовжки 80мм і відмічаємо точку К₀. Перпендикуляр з К₀ на m₁ дає нам точку К₁, потім по лінії проекційного зв'язку знаходимо точку К₂. З'єднуємо точку К з точками А,В,С на фронтальній та горизонтальній проекціях. Замiряємо та записуємо координати вершини пiрамiди

Рис.4 Рис.5

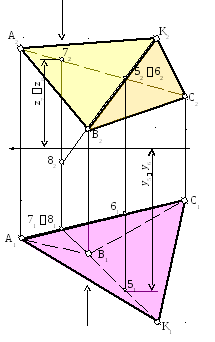
4. Для встановлення видимості ребер піраміди на фронтальній проекції , візьмемо на ребрах ВК і АС пару конкуруючих точок 5 і 6 (рис.5). На фронтальній проекції точка 5 закриває точку 6, так як у неї координата у більше (дивіться на горизонтальну проекцію цих точок), тому ребро ВК - видиме, а АС - невидиме.

Для встановлення видимості на горизонтальній проекції візьмемо конкуруючі точки 7 і 8 на ребрі АС і ВК. Точка 7 має координату z більшу ( дивіться на фронтальну проекцію цих точок), тобто точка 7 вище ніж точка 8, тому ребро АС - видиме, а ВК - невидиме.