
- •2015 Г.
- •2. Результаты обучения по дисциплине
- •3. Место дисциплины в структуре Образовательной программы высшего образования
- •4. Структура и содержание дисциплины
- •5. Формы контроля освоения дисциплины и фонд оценочных средств
- •6. Учебно-методическое и информационное обеспечение дисциплины
- •2015 Г.
- •8.1. Текущий контроль успеваемости
- •8.2. Рубежный контроль
- •1 Вариант
- •8.3. Промежуточный контроль
8.2. Рубежный контроль
Рубежная аттестация студентов производится по окончании каждой темы в форме защиты домашней контрольной работы.
Контрольная работа выполняется в соответствии с требованиями, представленными в методических указаниях: Кошкин, Ю. Г. Математика [Электронный вариант] : методические указания для студентов заочной формы обучения для выполнения контрольной работы / Ю. Г. Кошкин. – Красноярск: НОУ ВПО СИБУП, 2011. – 29 с.
Пример варианта контрольной работы:
1 Вариант
Вычислить матрицу
 ,
где
,
где ;
; ;
; .
.Вычислить определитель:

.
3. Вычислить обратную матрицу
 ,
если дана матрица
,
если дана матрица :
:
4. Решить системы линейных уравнений по формулам Крамера и методом Гаусса:
 .
.
5.
Найти производную функции:
6.
а) Используя метод разложения найти
интеграл:

б)
Используя метод замены переменной,
найти интегралы:

в) Используя метод интегрирования по частям, вычислить интегралы:
1.
 .
.
Критерии оценивания контрольной работы и её защиты:
правильное выполнение не менее 75% заданий – отлично,
правильное выполнение не менее 65% заданий – хорошо,
правильное выполнение не менее 50% заданий – удовлетворительно,
правильное выполнение менее 50% заданий – неудовлетворительно.
Контрольный тест
|
1.
Найти
A ∩ B, A
B = {-2, 0, 5, 7, 15} |
A ∩ B = { } A
A\B = { }, B\A = { } |
|
2. Какое из множеств содержится во всех приведенных |
1)
A 2) A ∩ B 3) A
|
|
3. Принято обозначать: N - множество натуральных чисел; Q - множество рациональных чисел; I –множество иррациональных чисел; Z - множество целых чисел; R - множество действительных чисел. Тогда не верным утверждением будет |
1)
7 |
|
4.
Предел
последовательности
|
1)3;
2) 2; 3) 1,5; 4) 0; 5)
|
|
5.
Значение
|
1)
|
|
6.
Значение
|
1)
0;
2) 2;
3)
|
|
7.
Значение
|
1)
|
|
8.
Функция
|
1) 0; 2) 5; 3) разрыва второго рода нет; 4)
|
|
9.
Значение производной функции
|
1)0;
2)- |
|
10.
Число точек экстремума функции
|
1) 2; 2) 3; 3) 1; 4) 0; 5) 4. |
|
11.
Значение
|
1)
1;2)
|
|
12.
Точками (точкой) перегиба для графика
функции
|
1)
-1; 2) 1; 3) -1 и 1; 4)
|
|
13.
Вертикальной асимптотой (асимптотами)
для графика функции
|
1) x = 3; 2) x = 1; 3) x = 0; x = 3. 4) x = 1 и x = 3; 5) x = 0 и x = 1. |
|
14.
Наклонной асимптотой для графика
функции
|
1) y = x+1 ; 2) нет наклонных асимптот ; 3) y= -x; 4) y = -x+1; 5) y = x |
|
15.
Одна из первообразных для функции
|
1) |
|
16.
Подстановка, которая сводит интеграл
|
1) |
|
17.
Значение интеграла
|
1)
1; 2) e;
3) 2;
4)
|
|
18.
Площадь фигуры, ограниченной графиком
функций
|
1)
20;
2)
|
|
19. Площадь заштрихованной области задана интегралом
|
|
|
20.
Вычисление несобственного интеграла
|
1)
интеграл расходится; 2)
|
Критерии оценивания контрольного теста:
удельный вес правильно выполненных заданий менее 50 % – 2 балла;
удельный вес правильно выполненных заданий от 50 % до 64 % – 3 балла
удельный вес правильно выполненных заданий от 65 % до 74% – 4 балла.
удельный вес правильно выполненных заданий свыше 75 % – 5 баллов.

 B,
A\B, B\Aдлямножеств
A = {-3, 0, 2,7,11},
B,
A\B, B\Aдлямножеств
A = {-3, 0, 2,7,11}, B
= {
}
B
= {
} B
4)В
5) A
B
4)В
5) A B
B C
C N
; 2) 10/2
N
; 2) 10/2 Z
; 3)
Z
; 3)
 I;
4)
I;
4)
 Q;
5)
Q;
5)
 I
I равен
равен .
. равно
равно ;
2)
;
2) ;
3)0;
4)
;
3)0;
4)
 ;
5)
;
5) .
. равно
равно ;
4)1;
5) 3.
;
4)1;
5) 3. равно
равно ;
2) 1; 3)
;
2) 1; 3) ;
4)
;
4) ;
5)0.
;
5)0. имеет разрывII–го
рода в точке х,
равной
имеет разрывII–го
рода в точке х,
равной ;
5) π/2.
;
5) π/2. в точкех=0
равно
в точкех=0
равно ;
3)
;
3) ;
4)-
;
4)- ;
5)1.
;
5)1. равно
равно равно
равно ;
3)2;
4)
;
3)2;
4)
 ;
5)10.
;
5)10. будут
будут и
и ;
5) 0.
;
5) 0. будет
будет будет
прямая
будет
прямая имеет вид
имеет вид 2)
2) 3)
3) 4)
4) 5)
5)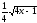 .
. к интегралу от рациональной функции,
имеет вид
к интегралу от рациональной функции,
имеет вид 2)
2) 3)
3) 4)
4) 5)
5) .
. ,
равно
,
равно ;
5)
;
5) .
. и осьюОХ
равна
и осьюОХ
равна 3)
-
3)
- ;
4)
;
4) 5) -
5) - .
.

 приводит к следующему результату
приводит к следующему результату 3)
3) 4)
4) 5)
5) .
.