Производная.

Производной функции называется придел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует:

.

Правила дифференцирования.

1. Производная постоянной равна нулю:

.

2. Производная аргумента равна 1:

.

3. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций:

.

4. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго:

.

5. Производная частного двух дифференцируемых функций находится по формуле:

, (если ).

6. Постоянный множитель можно выносить за знак производной:

.

Таблица производных элементарных функций.

1. .	6. .	11. .
2. .	7. .	12. .
3. .	8. .	13.
4. .	9. .
5. .	10. .

Производные сложной и обратной функции.

Пусть есть функция от независимой переменной ,определенной на промежутке с областью значений. Поставим в соответствие каждомуединственное значение , при котором .Тогда полученная функция ,определенная на промежутке с областью значений, называетсяобратной.

Дифференцирование обратной функции. Для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна обратной величине производной данной функции, т.е.

.

Пусть функция есть функция от переменной, определенной на множествес областью значений, а переменнаяв свою очередь является функциейот переменой, определенной на множествес областью значений. Тогда заданная на множествефункцияназываетсясложной функцией (или композицией функций, суперпозицией функций, функцией от функций).

Дифференцирование сложной функции. Если и– дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженной на производную самого промежуточного аргумента по независимой переменной, т.е.

.

Пример. Найти производные функций:

а); б); в); г); д)

Решение. а) Функцию можно представить в виде , где. Поэтому по формуле дифференцирования сложной функции

.

б) Имеем , где, поэтому получаем

.

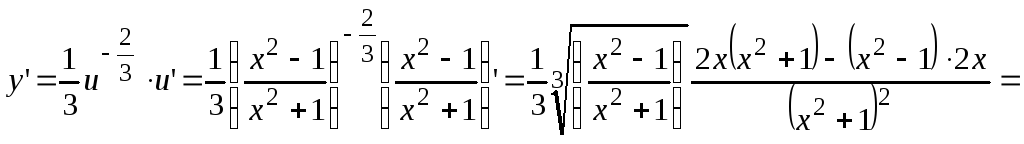
в) Вынося постоянный множитель 12 за знак производной, получим

.

г) Данная функция представляет произведение двух функций и, каждая из которых является сложной функцией (, где;, где). Поэтому

.

д) Представим функцию в виде . Теперь

.

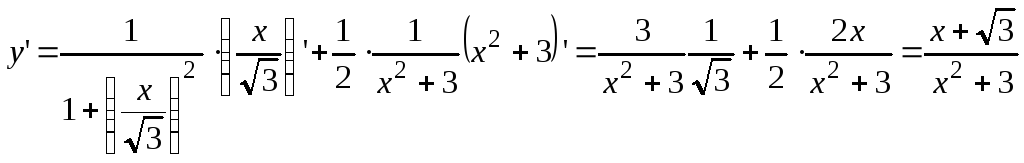Интегрирование.

Функция называетсяпервообразной функцией для функции на промежутке, если в каждой точкеэтого промежутка.

Совокупность всех первообразных для функции на промежуткеназываетсянеопределенным интегралом от функции и обозначается, где– знак интеграла,– подынтегральная функция,– подынтегральное выражение. Таким образом,

,

где – некоторая первообразная для,С – произвольная постоянная.

Свойства неопределенного интеграла.

1. Производная от неопределенного интеграла равна подынтегральной функции:

.

2. Дифференциал неопределенного интеграла равен подынтегральному выражению:

.

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.

.

4. Постоянный множитель можно выносить за знак интеграла:

.

5. Интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций:

.

Таблица интегралов от элементарных функций.

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.