
VYShMAT
.docx
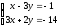 сызықтық
теңдеулер жүйесін шешіңіз: ((-4;
-1))
сызықтық
теңдеулер жүйесін шешіңіз: ((-4;
-1))
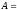
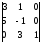 анықтауышын
есептеңіз( -8)
анықтауышын
есептеңіз( -8)
 анықтауышын
есептеңіз
(
-16)
анықтауышын
есептеңіз
(
-16)
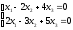 жүйені
шешіңіз.(
жүйені
шешіңіз.(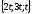 )
)
 анықтауышты
есептеңіз: (6)
анықтауышты
есептеңіз: (6)
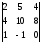 анықтауышын
есептеңіз (0)
анықтауышын
есептеңіз (0)
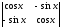 анықтауышын
есептеңіз: (
анықтауышын
есептеңіз: ( )
)
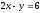 берілген
түзу теңдеуін кесіндіде жазыңыз: (
берілген
түзу теңдеуін кесіндіде жазыңыз: (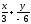 = 1)
= 1)
 болғанда
болғанда
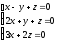 теңдеулер жүйесінің шешімін тауып,
жауапқа (x+y+z)
қосындысын жазыңыз :
(2)
теңдеулер жүйесінің шешімін тауып,
жауапқа (x+y+z)
қосындысын жазыңыз :
(2)
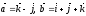 векторларына
тұрғызылған параллелограммның ауданын
есептеңіз:
векторларына
тұрғызылған параллелограммның ауданын
есептеңіз:
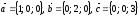 векторларына
тұрғызылған пирамиданың көлемін
табыңыз: (
1)
векторларына
тұрғызылған пирамиданың көлемін
табыңыз: (
1)
 векторларына
тұрғызылған үшбұрыштың ауданын табыңыз:
(
векторларына
тұрғызылған үшбұрыштың ауданын табыңыз:
( )
)
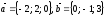 векторларына
тұрғызылған үшбұрыштың ауданын табыңыз:
векторларына
тұрғызылған үшбұрыштың ауданын табыңыз:
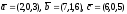 векторларының
аралас көбейтіндісін табыңыз:
(–5)
векторларының
аралас көбейтіндісін табыңыз:
(–5)
 векторына
перпендикуляр болатын
векторына
перпендикуляр болатын
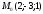 нүктесі арқылы өтетін жазықтық теңдеуінін
жазыңыз: (
нүктесі арқылы өтетін жазықтық теңдеуінін
жазыңыз: (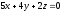 )
)
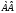 векторының
координаталарын табыңыз, егер А(6;
3; 4) және
В(4;7;3)
болса:
((-2;
4; -1)
векторының
координаталарын табыңыз, егер А(6;
3; 4) және
В(4;7;3)
болса:
((-2;
4; -1)
 гиперболасының
фокустарының арақашықтығын анықтау
керек: (10)
гиперболасының
фокустарының арақашықтығын анықтау
керек: (10)
 есептеңіз:
( -11)
есептеңіз:
( -11)
 жазықтығы:
(
жазықтығы:
(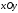 жазықтығына параллель
)
жазықтығына параллель
)
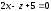 жазықтығының
нормаль векторының координаттарын
табу керек:
жазықтығының
нормаль векторының координаттарын
табу керек:
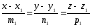 және
және
 түзулерінің параллельдік шартын
көрсетіңіз: (
түзулерінің параллельдік шартын
көрсетіңіз: (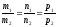 )
)
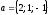 және
және
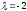 берілген. Табу керек
берілген. Табу керек
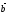 векторын, егер
векторын, егер
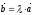 болса:
болса:
 және
және
 векторлары арасындағы
векторлары арасындағы
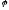 бұрышын табыңыз: (
бұрышын табыңыз: (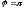 )
)
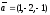 және
және
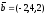 векторлары арасындағы
векторлары арасындағы
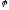 бұрышын табыңыздар:
бұрышын табыңыздар:
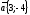 және
және
 векторлары берілген, олардың модулін
табыңыз: (
векторлары берілген, олардың модулін
табыңыз: (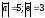 )
)
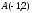 және
және
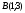 екі нүктесі арқылы өтетін түзудің
теңдеуі: (
екі нүктесі арқылы өтетін түзудің
теңдеуі: ( )
)
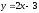 және
және
 екі түзуі қалай орналасқан? (өзара
перпендикуляр)
екі түзуі қалай орналасқан? (өзара
перпендикуляр)
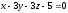 және
және
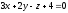 жазықтықтарының арасындағы бұрышты
табу керек: (900)
жазықтықтарының арасындағы бұрышты
табу керек: (900)
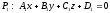 және
және
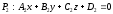 жазықтықтарының перпендикулярлық
шарты: (A1A2+B1B2+C1C2=0
)
жазықтықтарының перпендикулярлық
шарты: (A1A2+B1B2+C1C2=0
)
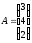 және
және
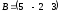 матрицалары берілген. Табу керек
матрицалары берілген. Табу керек
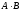 .
(
.
( )
)
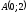 және
және
 нүктелерінің арақашықтығын табу керек
: (
нүктелерінің арақашықтығын табу керек
: (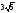 )
)
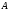 және
және
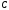 –
ның
қандай мәндерінде келесі екі түзу
параллель болады?
–
ның
қандай мәндерінде келесі екі түзу
параллель болады?
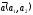 және
және
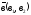 скалярлық көбейтіндісі деп келесі
санды айтамыз: (
скалярлық көбейтіндісі деп келесі
санды айтамыз: (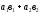 )
)
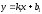 және
және
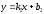 түзулерінің арасындағы бұрыш қай
формуламен анықталады?
түзулерінің арасындағы бұрыш қай
формуламен анықталады?
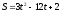 заңы
бойынша қозғалатын дененің қандай сәте
жылдамдығы нөлге тең?
заңы
бойынша қозғалатын дененің қандай сәте
жылдамдығы нөлге тең?
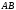 кесіндісін
кесіндісін
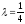 қатынасында бөлетін
қатынасында бөлетін
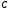 нүктесінің координаталарын табыңыз,
егер
нүктесінің координаталарын табыңыз,
егер
 және
және
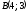 болса: ((-4;
-1 )
болса: ((-4;
-1 )
 кесіндісінің
ортасының координатасын табыңыз, егер
А(3; 6) және В(5; 2) болса: ((4;
4))
кесіндісінің
ортасының координатасын табыңыз, егер
А(3; 6) және В(5; 2) болса: ((4;
4))
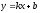 көлбеу
асимптотасын табу формуласын көрсетіңіз:
көлбеу
асимптотасын табу формуласын көрсетіңіз:
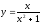 қисығына
қисығына
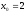 нүктесінде
тұрғызылған жанама теңдеуін жазыңыз:
нүктесінде
тұрғызылған жанама теңдеуін жазыңыз:
 матрицасы
матрицасы
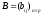 матрицасына көбейтілген. С=АВ
матрицасының
матрицасына көбейтілген. С=АВ
матрицасының
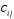 элементерінің есептелу теңдігін табыңыз
элементерінің есептелу теңдігін табыңыз
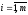 ;
;
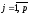 :
(
:
(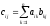 .)
.)
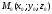 нүктесі
арқылы өтетін және
нүктесі
арқылы өтетін және
 векторына перпендикуляр жазықтық
теңдеуі: (
векторына перпендикуляр жазықтық
теңдеуі: (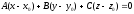 )
)
 нүктесінен
нүктесінен
 жазықтығына дейінгі
жазықтығына дейінгі
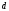 арақашықтығын есептеңіз:
арақашықтығын есептеңіз:
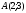 нүктесінен
нүктесінен
 түзуіне дейінгі арақашықтықты табыңыз:
(1,6
)
түзуіне дейінгі арақашықтықты табыңыз:
(1,6
)
 -
ның қандай мәнінде
-
ның қандай мәнінде
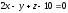 және
және
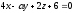 жазықтықтары параллель болады? (
жазықтықтары параллель болады? (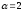 )
)
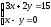 сызықтық
теңдеулер жүйесін шешіңіз: ((3;3))
сызықтық
теңдеулер жүйесін шешіңіз: ((3;3))
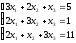 теңдеулер
жүйесін шешіңіз: (
теңдеулер
жүйесін шешіңіз: (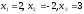 )
)
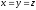 теңдеуі...анықтайды:
(Кеңістіктегі
түзуді)
теңдеуі...анықтайды:
(Кеңістіктегі
түзуді)
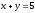 түзуіне
қай нүкте жатады? ((2;
3))
түзуіне
қай нүкте жатады? ((2;
3))
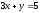 түзуіне
қандай түзу параллель:
(
түзуіне
қандай түзу параллель:
(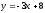 )
)
 түзуінің
түзуінің
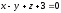 жазықтығымен қиылысу нүктесін табыңыз:
жазықтығымен қиылысу нүктесін табыңыз:
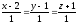 түзуінің
түзуінің
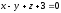 жазықтығымен қиылысу нүктесін табыңыз:
жазықтығымен қиылысу нүктесін табыңыз:
 үш
белгісізден тұратын, үш теңдеулер
жүйесінің матрицалық шешімі келесі
түрде жазылады:
(
үш
белгісізден тұратын, үш теңдеулер
жүйесінің матрицалық шешімі келесі
түрде жазылады:
(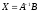 )
)
 функцияның
анықталу облысын табыңыз: (
функцияның
анықталу облысын табыңыз: ( )
)
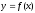 функциясы
функциясы
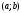 аралығында өспелі деп аталады, егер
ол...: (осы
аралықта тек оң
аралығында өспелі деп аталады, егер
ол...: (осы
аралықта тек оң
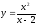 функциясы
берілген. Берілген функцияның иілу
нүктесін анықтаңыз: (иілу
нүктесі
жоқ
)
функциясы
берілген. Берілген функцияның иілу
нүктесін анықтаңыз: (иілу
нүктесі
жоқ
)
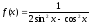 функциясын
интегралдау үшін қандай айнымалыны
ауыстыру қолданылады?
(
функциясын
интегралдау үшін қандай айнымалыны
ауыстыру қолданылады?
( )
)
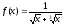 функциясын
интегралдау үшін, қандй айнымалыны
ауыстыруды қолданамыз? (
функциясын
интегралдау үшін, қандй айнымалыны
ауыстыруды қолданамыз? (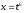 )
)
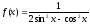 функциясын
қандай ауыстыру арқылы интегралдаймыз:
(
функциясын
қандай ауыстыру арқылы интегралдаймыз:
(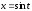 )
)
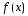 функциясының
анықталмаған интегралы деп оның ....
айтамыз: (барлық
алғашқы функцияларының жиынын.)
функциясының
анықталмаған интегралы деп оның ....
айтамыз: (барлық
алғашқы функцияларының жиынын.)
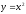 функциясының
графигіне
функциясының
графигіне
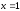 нүктесінде тұрғызылған жанама теңдеуін
табыңыз:
нүктесінде тұрғызылған жанама теңдеуін
табыңыз:
 функциясының
графигінің ойық және дөңес аралығын
табыңыз: ((-
функциясының
графигінің ойық және дөңес аралығын
табыңыз: ((-
 ;
0)
дөңес
және (0;
;
0)
дөңес
және (0; )
ойық )
)
ойық )
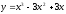 функциясының
дифференциалын табыңыз: (
функциясының
дифференциалын табыңыз: (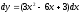 )
)
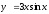 функциясының
екіші ретті туындысын табыңыз: (
функциясының
екіші ретті туындысын табыңыз: (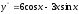 )
)
 функциясының
қанша асимптотасы бар? (1)
функциясының
қанша асимптотасы бар? (1)
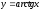 функциясының
туындысын есептеңіз: (
функциясының
туындысын есептеңіз: (
 )
)
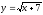 функциясының
туындысын есептеңіз: (
функциясының
туындысын есептеңіз: (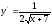 )
)
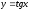 функциясының
туындысын табыңыз: (
функциясының
туындысын табыңыз: ( )
)
 функциясының
туындысын табыңыз: (
функциясының
туындысын табыңыз: (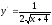 )
)
 функциясының
тік асимптотасын табыңыз: (
функциясының
тік асимптотасын табыңыз: ( )
)
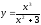 функциясының
тік асимптотасын табыңыз: (тік
асимптотасы жоқ)
функциясының
тік асимптотасын табыңыз: (тік
асимптотасы жоқ)
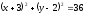 шеңберінің
центрі мен радиусын табу керек:
(
шеңберінің
центрі мен радиусын табу керек:
(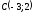 ,
,
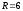 )
)
(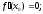 )
)
(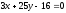 )
)
(
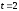 )
)
(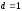 )
)
(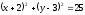 )
)
(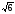 )
)
(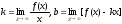 )
)
(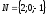 )
)
( -3)
((-1;-2;-4))
(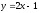 )
)
(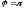 )
)
(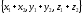 )
)
(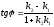 )
)
( )
)
(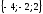 )
)
(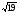 )
)
(-1;-2;-4))
(2, 3, 5 )
(-3;
4) нүктесінен
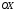 өсіне дейінгі арақашықтықты табыңыз?
(4)
өсіне дейінгі арақашықтықты табыңыз?
(4)
(теріс мән қабылдайды)
 ,
,
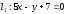 ,
,
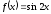 ,
есептеу керек:
,
есептеу керек:
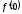 (2
)
(2
)
 ,
есептеу керек:
,
есептеу керек:
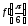 .
(
3)
.
(
3)
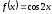 ,
есептеу керек:
,
есептеу керек:
 .
(
-4)
.
(
-4)
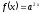 ,
есептеу керек:
,
есептеу керек:
 .
(
.
( )
)
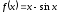 ,
есептеу керек:
,
есептеу керек:
 .
(1)
.
(1)
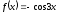 ,
есептеу керек:
,
есептеу керек:
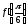 .
(3 )
.
(3 )
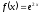 ,
есептеу керек:
,
есептеу керек:
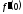 .
(4)
.
(4)
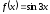 ,
есептеу керек:
,
есептеу керек:
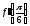 .(
-9)
.(
-9)
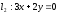 .
.
 .
Табу керек
.
Табу керек
 : (
42)
: (
42)
 .
()
.
()
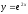 .
Табу
керек
.
Табу
керек
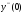 ( 8
)
( 8
)
1)
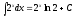 ,
2)
,
2)
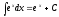 ,
3)
,
3)
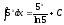 ,
,
4)
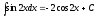 ,
5)
,
5)
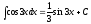 .
.
А(2;1)
нүктесінен 3x-6y+5=0 түзуіне түсірілген
перпендикулярдың ұзындығын табыңыз:
(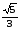 )
)
Айнымалыны
алмастыру арқылы интегралдау: ( мұндағы
мұндағы
 )
)
Айталық
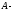 теңдеулер
жүйесінің негізгі матрицасы, ал
теңдеулер
жүйесінің негізгі матрицасы, ал
 кеңейтілген
матрицасы болса, берілген теңдеулер
жүйесі үйлесімді тек, тек сонда ғана:
(rang
A = rang B)
кеңейтілген
матрицасы болса, берілген теңдеулер
жүйесі үйлесімді тек, тек сонда ғана:
(rang
A = rang B)
Анықтауышты
есептеңіз
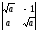 :
(2a)
:
(2a)
Анықтауышты
есептеңіз
 :
(
70)
:
(
70)
Анықтауыштың
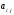 элементінің алгебралық толықтауышы
деп....: (
элементінің алгебралық толықтауышы
деп....: (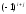 шамасына көбейтілген
шамасына көбейтілген
 элементінің миноры.)
элементінің миноры.)
Берілген
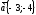 және
және
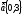 векторларының модулін анықтаңыздар:
(
векторларының модулін анықтаңыздар:
( )
)
Берілген
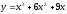 функциясының иілу нүктесін табыңыз:
((-2;-2))
функциясының иілу нүктесін табыңыз:
((-2;-2))
Берілген екі түзудің арасындағы бұрышты табу керек:
Берілген
матрицаның кері матрицасы
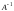 -
ді табу
керек:
-
ді табу
керек:
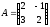 .
(
.
( )
)
Берілген
матрицаның кері матрицасы
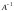 -
ді табу
керек:
-
ді табу
керек:
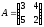 .
(
.
(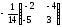 )
)
Берілген
матрицаның кері матрицасы
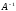 -
ді табу
керек:
-
ді табу
керек:
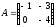 .
(
.
(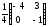 )
)
Берілген
нүктелердің қайсысы
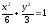 эллипсінде жатады? (2;
1)
эллипсінде жатады? (2;
1)
Берілген
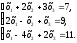 теңдеулер
жүйесінің анықтауышы –25 болатынын
қолданып,
теңдеулер
жүйесінің анықтауышы –25 болатынын
қолданып,
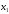 табыңыз. (3
)
табыңыз. (3
)
Бөліктеп
интегралдау формуласы: ( мұндағы
мұндағы
 дифференциалданатын
функция)
дифференциалданатын
функция)
Векторлардың
скалярлық көбейтіндісін табыңыз
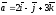 және
және
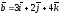 : (16)
: (16)
Векторлардың
скалярлық көбейтіндісін табыңыз
 және
және
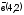 .
(18)
.
(18)
векторының
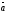 векторына скаляр көбейтіндісі тең:
(
векторына скаляр көбейтіндісі тең:
(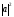 )
)
Декарттық
координаттар жүйесінде
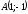 және
және
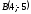 екі нүктесі берілген.
екі нүктесі берілген.
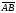 векторының координатасын анықтаңыз:
(3;-4)
векторының координатасын анықтаңыз:
(3;-4)
Дұрыс
теңдікті табыңыз: (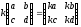 )
)
Дұрыс
формуланы көрсетіңіз:
(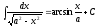 )
)
Дұрыс
формуланы көрсетіңіз: ( )
)
Егер
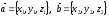 болса,
болса,
 векторының координатасын табыңыз:
векторының координатасын табыңыз:
Егер
ax+by+c=0
жазықтықтағы түзу теңдеуі болса,
онда....:
(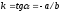 )
)
Егер
ax+by+c=0
жазықтықтағы түзу теңдеуі болса,
онда...: (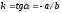 )
)
Егер
 болса, онда
болса, онда
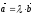 шартын қанағаттандыратын
шартын қанағаттандыратын
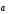 және
және
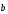 векторлары: (бағыттас)
векторлары: (бағыттас)
Егер
 болса, табу керек
болса, табу керек
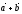 :
(
:
(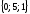 )
)
Егер
 нүктесінде
нүктесінде
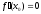 ,
ал
,
ал
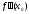 бар және
бар және
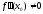 болса, онда бұл нүктеде .... теңсіздігі
орындалса функцияның максимумы болады.(
болса, онда бұл нүктеде .... теңсіздігі
орындалса функцияның максимумы болады.(
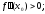 )
)
Егер
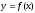 функциясының екінші туындысы қандайда
бір аралықта теріс болса, онда осы
аралықта мұндай функцияның графигі:
(дөңес.)
функциясының екінші туындысы қандайда
бір аралықта теріс болса, онда осы
аралықта мұндай функцияның графигі:
(дөңес.)
Егер анықтауышта екі параллель қатардың орындарын ауыстырса, онда анықтауыш...:
Егер анықтауыштың екі қатары бірдей болса, онда....: (Анықтауыш нөлге тең)
Егер
анықтауыштың қандайда бір жатық жолына
(тік жолына) басқа жатық жолдың (тік
жолдың) сәйкес элементтерін
 көбейтіп қосатын болсақ, онда анықтауыш:
(өзгермейді )
көбейтіп қосатын болсақ, онда анықтауыш:
(өзгермейді )
Егер
барлық
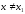 және
және
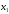 жуық мәндер үшін .... теңсіздігі орындалса,
онда
жуық мәндер үшін .... теңсіздігі орындалса,
онда
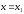 болғанда
болғанда
 функциясының минимумы бар болады: (
функциясының минимумы бар болады: (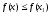 )
)
Егер
барлық
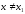 және
және
 жуық мәндері үшін .... теңсіздігі орындалса
жуық мәндері үшін .... теңсіздігі орындалса
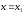 болғанда
болғанда
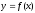 функциясының максимумы бар болады. (
)
функциясының максимумы бар болады. (
)
Егер
барлық
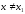 және
және
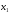 жуық мәндері үшін .... теңсіздігі орындалса
жуық мәндері үшін .... теңсіздігі орындалса
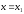 болғанда
болғанда
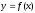 функциясының максимумы бар болады. (
функциясының максимумы бар болады. (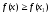 )
)
Егер
векторлар
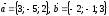 ,
табу
керек
,
табу
керек
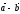 :
(
:
(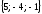 )
)
Егер
дифференциалданатын
 функциясының
функциясының
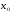 нүктесінде экстремум
бар
болса, онда:
нүктесінде экстремум
бар
болса, онда:
Егер екі вектордың скалярлық көбейтіндісі нөлге тең болса, онда бұл векторлар: (перпендикулярлы)
Егер
нүкте
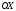 жатса, онда оның ординатасы тең: (0)
жатса, онда оның ординатасы тең: (0)
Егер
нүкте
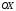 өсінде жатса, онда оның ординатасы тең:
(0)
өсінде жатса, онда оның ординатасы тең:
(0)
Егер
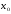 нүктесінде
функцияның бір біріне тең емес ақырғы
бір жақты шектері бар болса, онда функция
ол нүтеде : (үзіліссіз)
нүктесінде
функцияның бір біріне тең емес ақырғы
бір жақты шектері бар болса, онда функция
ол нүтеде : (үзіліссіз)
Екі вектор тең, егер...: ( векторлардың модулдері тең, коллинеарлы және бағыттас болса)
Екі вектор тең, егер...: (векторлардың модулдері тең, коллинеарлы және бағыттас болса)
Екі
нүкте арқылы өтетін түзу теңдеуі: (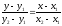 .)
.)
Есептеңіз
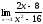 : (
: ( )
)
Есептеңіз
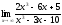 : (
2)
: (
2)
Есептеңіз
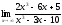 : (
2)
: (
2)
Есептеңіз
 :
(
:
( )
)
Есептеңіз

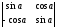 : (
1)
: (
1)
Есептеңіз
 : (
29)
: (
29)
Есептеңіз
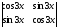 :
(cos6x
)
:
(cos6x
)
Есептеңіз
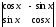 :
(1)
:
(1)
Есептеу
керек
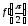 :
:
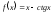 .
(
2)
.
(
2)
Жазықтықтағы
түзулердің параллельдік шарты келесі
түрде болады:
( )
)
Жазықтықтың
жалпы теңдеуі келесі түрде жазылады :
(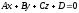 )
)
Интегралды
табыңыз
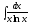 (
(
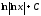 )
)
Интегралды
табыңыз
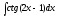 (
(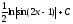 )
)
Интегралды
табыңыз
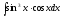 :
(
:
( )
)
Интегралды
табыңыз
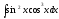 :
(
:
(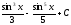 )
)
Интегралды
табыңыз
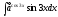 :
(
-
:
(
-
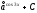 .
)
.
)
Интегралды
табыңыз
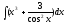 :
(
:
(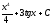 )
)
Интегралды
табыңыз
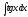 :
(
:
(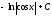 )
)
Интегралды
табыңыз
 :
(
:
(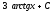 )
)
Интегралды
табыңыз:
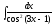 : (
: (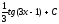 )
)
Интегралды
табыңыз:
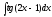 :
(
:
( )
)
Интегралды
табыңыз:
 :
(
:
(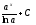 )
)
Интегралды
табыңыз:
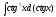 :
(
:
( )
)
Интегралды
табыңыз:
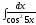 .
(
.
(![]() )
)
Интегралды
табыңыз:
 :
(
:
(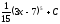 )
)
Интегралды
табыңыз:
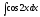 :
(
:
( )
)
Интегралды
табыңыз:
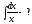 :
(
:
(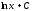 )
)
Интегралды
табыңыз:
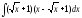
 :
(
:
( )
)
Интегралды
табыңыз:
 :
(
:
(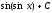 )
)
Интегралды
табыңыз: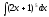 :
(
:
(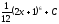 )
)
Интегралын
табыңыз:
 : (
: (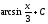 )
)
Интегралын
табыңыз:
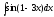 :
(
:
( )
)
Интегралын
табыңыз:
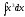 :
(
:
(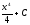 )
)
Келесі теңдеулердің қайсысы дұрыс?
Келесі
теңдеулердің қайсысы дұрыс? ( )
)
Келесі
теңдеулердің қайсысы дұрыс? (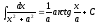 )
)
Келесі
теңдіктердің қайсысы дұрыс?: 1)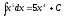 2)
2)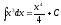 3)
3)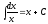 4)
4)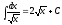 5)
5)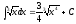 (2,4,5
)
(2,4,5
)
Көрсетілген
түзулердің қайсысы
 түзуіне перпендикуляр? (
түзуіне перпендикуляр? ( )
)
Матрицаның миноры деп...: (Дұрыс жауап жоқ)
мәндер қабылдаса.)
Нөлдік вектор деп .... векторды айтамыз: (басы және соңы беттесетін)
Нүктелердің
қайсысы
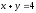 түзуінде жатады?(
(2; 2))
түзуінде жатады?(
(2; 2))
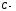 ның
қандай мәнінде
ның
қандай мәнінде
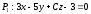 және
және
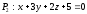 жазықтықтары перпендикуляр? (
6)
жазықтықтары перпендикуляр? (
6)
 ның
қандай мәнінде
ның
қандай мәнінде
 және
және
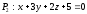 жазықтықтары перпендикуляр? (
–9)
жазықтықтары перпендикуляр? (
–9)
 -ның
қандай мәнінде
-ның
қандай мәнінде
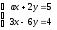 теңдеулер жүйесінің шешімі болмайды?(
–1)
теңдеулер жүйесінің шешімі болмайды?(
–1)
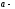 ның
қандай мәнінде
ның
қандай мәнінде
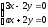 теңдеулер жүйесінің шешімі нөлге тең
емес?
теңдеулер жүйесінің шешімі нөлге тең
емес?
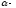 ның
қандай мәнінде
ның
қандай мәнінде
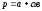 ,
,
 векторлар жұбы коллинеарлы болады,
егер
векторлар жұбы коллинеарлы болады,
егер
 ,
,
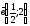 ?
(
0)
?
(
0)
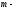 нің
қандай мәнінде
нің
қандай мәнінде
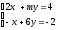 жүйесі анықталмаған?(
-12)
жүйесі анықталмаған?(
-12)
Ордината
өсінде
 түзуде жататын нүктені табыңыз, егер
А(-2; 0) және В(3;3): ((0;
6/5))
түзуде жататын нүктені табыңыз, егер
А(-2; 0) және В(3;3): ((0;
6/5))
Радиусы
5, центрі
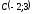 нүктесінде жатқан шеңбердің теңдеуін
табу керек:
нүктесінде жатқан шеңбердің теңдеуін
табу керек:
Сызықтармен
шектелген фигураның ауданын табыңыз
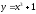 ,
,
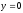 ,
,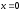 ,
,
 :
(6 )
:
(6 )
Сызықтық теңдеулер жүйесі үйлесімді деп аталады, егер оның....(ең кемінде бір шешімі бар болса)
Теңдеуді
шешіңіз
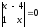 : (
: (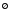 .)
.)
Теңдеулер
жүйесін шешіп, жауабына (2x+y)
нәтижесін жазыңыз.
 :
(
4)
:
(
4)
Теңдеулердің
қайсысы жазықтықтағы түзудің жалпы
теңдеуі?
( )
)
Төменде
берілген қандай гиперболаның a=2;
b=1
тең? (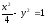 )
)
Төменде
көрсетілген гиперболаның қайсысында
a=4;
b=3?:
(
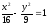 )
)
Төменде
көрсетілген эллипстердің қайсысында
a=2;
b=5
? (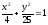 )
)
Төменде
көрсетілген эллипстердің қайсысында
a=4;
b=3?:
(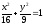 )
)
Тік
бұрышты декарттық базисте
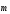 векторының координаталарын анықтаңыз,
егер
векторының координаталарын анықтаңыз,
егер
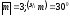 :
(
:
(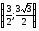 )
)
у=2х+3
түзуі
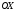 өсін қандай бұрышпен қиады?
(
өсін қандай бұрышпен қиады?
( )
)
Үйлесімді теңдеулер жүйесінің ... бар болады. (Бір немесе бірнеше шешімі)
Үш вектор компланарлы, егер олар....: (бір жазықтыққа параллель болса )
Функция дифференциалының анықтамасын көрсетіңіз: (функцияның дифференциалы, берілген функцияның туындысын тең )
Функцияның
туындысын табыңыз :
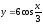 .
(
.
( )
)
Шекті
есептеңіз:
 : (–
: (–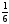 )
)
Шекті
есептеу керек ( Лопиталь ережесі бойынша
):
 .
(
.
(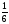 )
)
Шекті
есептеу керек:
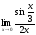 .
(
.
( )
)
Шекті
есептеу керек:
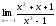 .(
.(
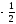 )
)
Шекті
есептеу
керек:
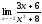 :
(
:
(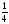 )
)
Шекті
табыңыз:
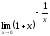 : (
: (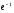 )
)
Шекті
табыңыз:
 :
(
:
( )
)
Шекті
табыңыз:
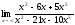 : (–0,5
)
: (–0,5
)
Шекті
табыңыз:
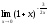 :(
:(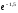 )
)
Эллипстің
жарты өстері
 және
және
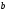 –ны
табу керек:
–ны
табу керек:
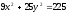 .
(
.
(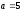 ,
,
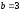 )
)
