Таблиця 5.33

Трактор	Продуктивність трактора в господарстві, еталонних гектарів на добу
	І господарство	ІІ господарство	ІІІ господарство
«Бєларусь», МТЗ-80	50	63	59
ЮМЗ-6АЛК	49	56	50
MEZZO 6100	61	58	62

Визначити оптимальний розподіл техніки по господарствах.

Для розв’язування задачі скористаємось методом потенціалів. Задача належить до відкритого типу транспортних задач, бо кількість наявної техніки дорівнює 23 одиницям, а потреби — 20 одиницям, тому необхідно ввести фіктивного споживача (четверте господарство) з потребою, що дорівнює 3 одиницям техніки.

Всі значення продуктивностей техніки з наведеної таблиці використовуватимемо, розв’язуючи задачу, з протилежним знаком.

Застосовуючи метод потенціалів, отримаємо оптимальний план розподілу техніки, що наведений у табл. 5.34.

Таблиця 5.34

Трактор	Продуктивність трактора в господарстві, етал. га на добу
	І господарство (10 один.)	ІІ господарство (5 один.)	ІІІ господарство (5 один.)	ІV господарство (фіктивне) (3 один.)
«Бєларусь», МТЗ-80 (8 один.)	–50	–63 3	–59 5	0
ЮМЗ-6АЛК (10 один.)	–49 5	–56 2	–50	0 3
MEZZO 6100 (5 один.)	–61 5	–58	–62	0

За оптимальним планом кожне господарство отримує потрібну кількість тракторів. Однак, оскільки задача належить до відкритого типу, значення відповідає фіктивно введеному споживачеві. Це означає, що трактори ЮМЗ-6АЛК будуть розподілені не повністю. З десяти їх одиниць розподілено тільки 7.

Загальне значення продуктивності тракторів становить 1146 ета­лонних гектарів на добу.

Задача про призначення. Потрібно виконати n видів робіт, на які претендують n кандидатів. Витрати на оплату праці i-го кандидата за виконання j-ої роботи дорівнюють . Кожен кандидат може бути призначений лише на одну роботу, і кожна робота має виконуватися лише одним кандидатом. Потрібно знайти оптимальне призначення кандидатів на виконання робіт, за якого сумарні витрати на виконання всіх робіт будуть мінімальними.

Нехай дорівнює одиниці, якщоi-ий кандидат виконує j-ту роботу, та дорівнює нулю в протилежному разі. Тоді умову, що кожен кандидат має виконувати лише одну роботу, запишемо у вигляді: . Умова виконання кожної роботи лише одним канди­датом має вигляд:. Цільова функція має такий вираз:. Отже, маємо математичну модель транспортної задачі:

min

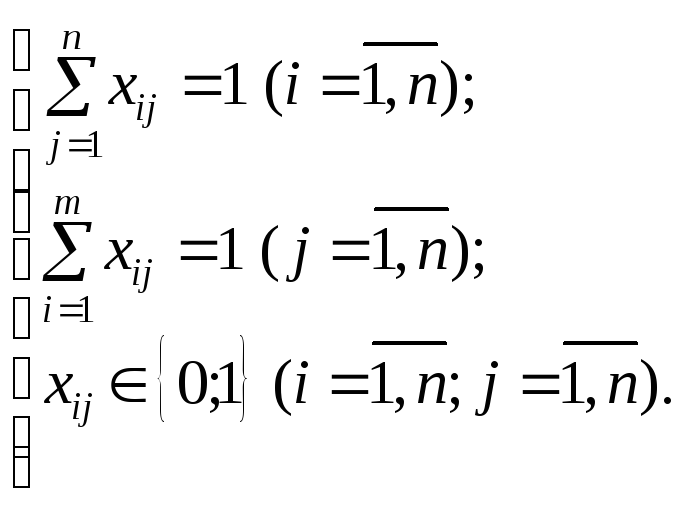
Найзручнішим методом розв’язання задачі про призначення є угорський метод.

Розглянемо приклад економічної постановки задачі про призначення.

Науково-дослідний інститут отримав замовлення на виконання чотирьох дослідних проектів. Кінцеві результати першого проекту є початковими даними для другого проекту, а кінцеві результати другого проекту — початковими для третього і, нарешті, результати третього проекту є початковими значеннями для четвертого. Виконавцями проектів можуть бути чотири відділи інституту. Кожен відділ визначив кількість часу, яка необхідна для виконання ним науково-дослідних робіт. Матриця витрат часу має вигляд:

.

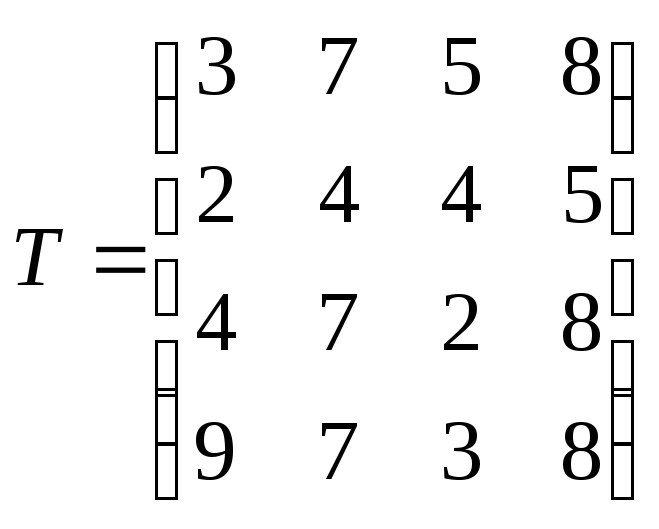Кожен елемент а_ij матриці Т означає тривалість виконання i-им відділом j-го проекту. Витрати часу наведені в тижнях. Необхідно так вибрати відділи, які будуть працювати над проектами, щоб тривалість виконання всіх проектів була мінімальною.

Для розв’язування задачі вводимо змінні: , якщоi-ий відділ призначено для виконання j-го проекту; та в протилежному разі.

Розв’язуючи задачу угорським методом, матимемо два альтер­нативні оптимальні плани. Перший оптимальний план:

,

тобто перший відділ слід призначити для виконання першого проекту ();

другий відділ — для виконання другого проекту ();

третій відділ — для виконання третього проекту ();

а четвертий відділ — для виконання четвертого проекту ().

За такого розподілу виконавців загальна тривалість виконання чотирьох проектів дорівнюватиме:

.

Другий оптимальний план:.

В такому разі тривалість виконання всіх проектів також дорів­нюватиме 17 тижням:

.

Заключні зауваження

Практичне застосування класичної економіко-математичної моделі транспортної задачі наштовхується на певні труднощі. Насамперед, як правило, необхідно перевозити неоднорідні продукти. Тоді транспортна задача ускладнюється. Економіко-математичну модель для багатопродуктової транспортної задачі запишемо так:

за умов: ,

;

,

;

,

де k — вид продукції, яку треба перевезти.

Часто господарські зв’язки між постачальниками і споживачами вимагають відповідних обмежень:

;

,

де М₁, М₂ — відповідні множини індексів i, j, за якими вводяться обмеження на обсяги перевезень і-ї продукції до j-го споживача. Обмеженнями гарантується, що відповіднийj-й споживач отримає і-ї продукції не менше від заданого обсягу. Обмеженнями виду описують транспортні можливості.

У класичній транспортній задачі, як правило, критерієм оптимальності є мінімізація транспортних витрат, тобто розв’язується задача на мінімум. Проте на практиці бувають випадки, коли необхідно знайти максимум цільової функції. Наприклад, необхідно розподілити робітників (верстати) між окремими видами робіт, щоб отримати максимальну сумарну продуктивність праці. Подібна ситуація має місце за оптимізації розміщення сільськогосподарських культур на ділянках землі різної якості. У такому разі критерієм оптимальності є максимізація вартості вирощеної (валової) продукції.

У класичній транспортній задачі допускається, що витрати на транспортування лінійно залежать від обсягів перевезень. Але на практиці ця умова порушується, тобто такі зв’язки, як правило, є нелінійними, стохастичними тощо. Особливої уваги заслуговує така постановка транспортної задачі, в якій необхідно мінімізувати тривалість виконання заданих обсягів робіт, наприклад, перевезення сировини та продукції, яка швидко псується. Цей критерій часто використовується для оптимізації військових операцій, виконання сільськогосподарських робіт (наприклад, збору урожаю) тощо.

Транспортна задача значно ускладнюється за моделювання виробничо-транспортних економічних систем, які виробляють продукцію в широкому асортименті, а для перевезення її застосовують різні види транспорту.

Контрольні запитання

1. Опишіть економічну і математичну постановку класичної транспортної задачі.

2. Чим відрізняється транспортна задача від загальної задачі лінійного програмування?

3. Сформулюйте необхідну і достатню умови існування розв’язку транспортної задачі.

4. Які ви знаєте властивості опорних планів транспортної задачі?

5. Чим відрізняється відкрита транспортна задача від закритої?

6. Як перетворити відкриту транспортну задачу на закриту?

7. Які ви знаєте методи побудови опорного плану?

8. Побудуйте невироджений опорний план методом північно-західного кута: для задачі:

a_i = 50, 70, 90; b_j = 70, 65, 70, 75.

9. Що означає «виродження» опорного плану? Як його позбутися?

10. Назвіть етапи алгоритму методу потенціалів.

11. Як обчислюють потенціали?

12. Назвіть умови оптимальності транспортної задачі.

13. Опишіть економічну і математичну постановку двохетапної транспортної задачі.

14. Назвіть особливості розв’язування транспортних задач з обмеженнями виду .

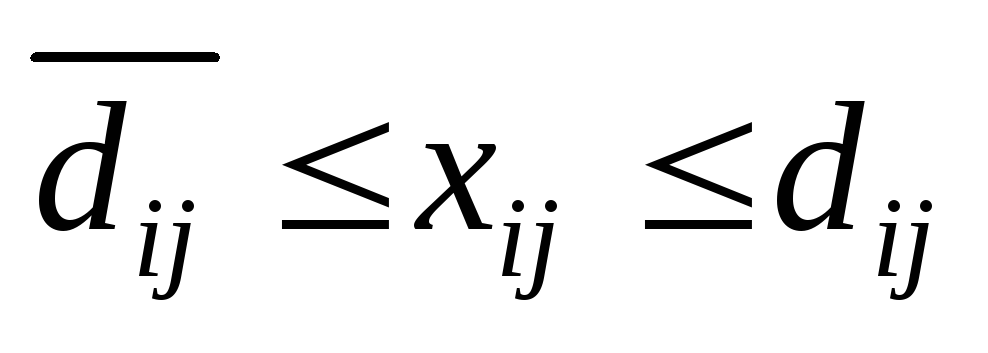Приклади та завдання для самостійної роботи

Розв’язати наведені нижче транспортні задачі:

Задача 5.1.

ai = (8; 10; 5); bj = (5; 5; 10);

.

Задача 5.2.

ai = (8; 7; 6); bj = (7; 10; 6);

.

Задача 5.3.

ai = (15; 10; 5; 20); bj = (10; 20; 15);

.

Задача 5.4.

ai = (10; 20; 40); bj = (30; 10; 60).

.

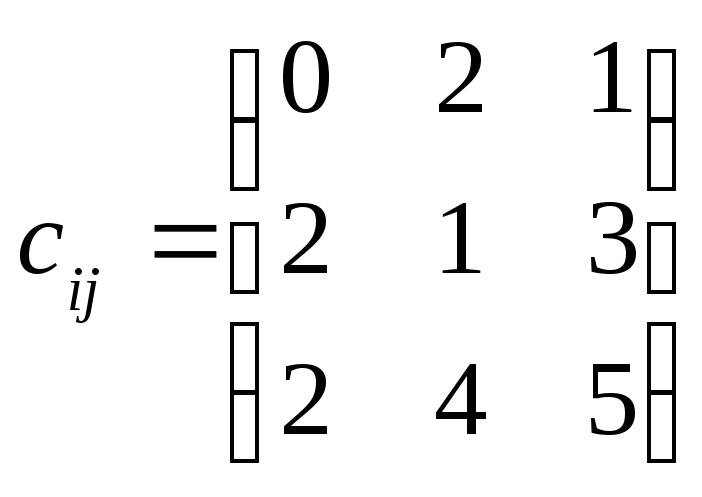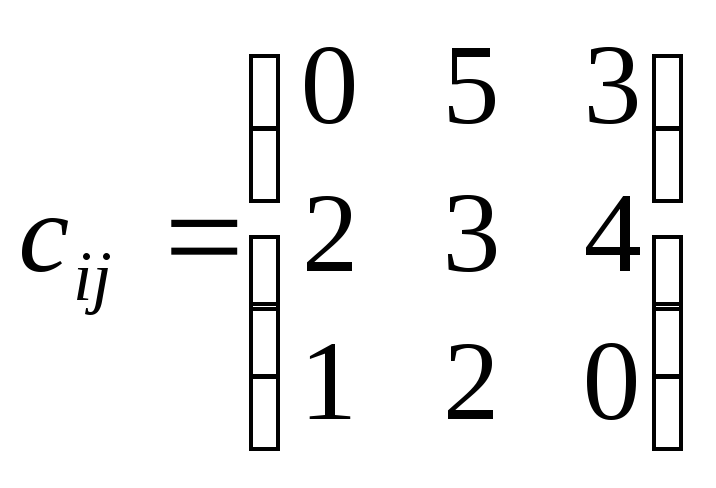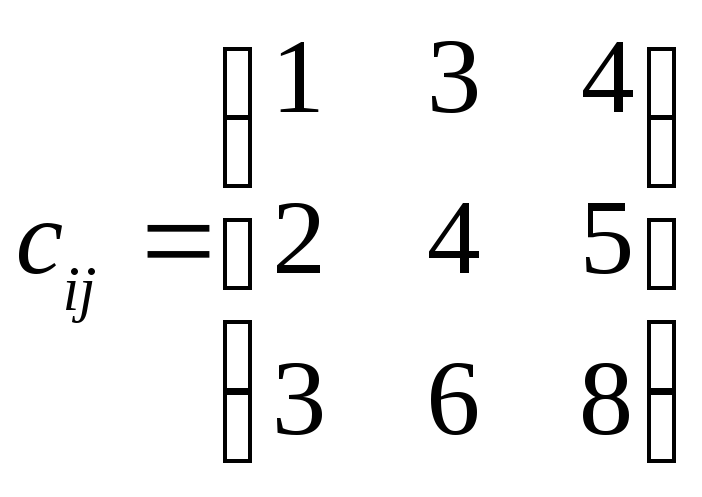255