8.8.1. Квадратична форма та її властивості

Квадратична функція n змінних називається квадратичною формою і може бути подана у вигляді:

,

де , , ,

причому матриця С завжди симетрична, тобто для всіх .

Квадратична форма Z(X) називається від’ємно означеною, якщо для всіх Х, крім Х = 0, значення Z(X) < 0 (якщо Z(X) ≤ 0, то маємо від’ємно напівозначену квадратичну форму), у протилежному разі Z(X) є додатно означеною (якщо Z(X) ≥ 0, то маємо додатно напівозначену квадратичну форму).

Квадратична форма Z(X) називається неозначеною, якщо вона додатна для одних значень Х і від’ємна для інших.

Вид квадратичної форми можна визначити, використовуючи

— вектор характеристичних коренів (власних значень) матриці С.

Вектор характеристичних коренів матриці С є вектором, кожна компонента якого задовольняє систему рівнянь виду . Система має ненульовий розв’язок, якщо . Таке рівняння називається характеристичним рівнянням матриці С і має коренів, які утворюють вектор :

.

Наведемо без доведення теорему (доведення можна знайти в літературі [19]).

Теорема 8.5. Для того, щоб довільна квадратична форма була додатно (від’ємно) означеною, необхідно і достатньо, щоб усі компоненти вектора характеристичних коренів були додатними (від’ємними) значеннями.

Якщо хоча б один із характеристичних коренів дорівнює нулю, то квадратична форма є напівдодатною (напіввід’ємною). Якщо корені мають різні знаки, то квадратична форма є неозначеною.

Визначити вид квадратичної форми:

Матриця С має вигляд:

.

Запишемо характеристичне рівняння .

Звідси маємо:

.

Коренями отриманого квадратного рівняння є: , тоді . Отже, квадратична форма за теоремою 8.5 є напіввід’ємною.

8.8.2. Метод розв’язування задач квадратичного програмування

Зазначимо, що відомим з теорії аналізу функцій є таке твердження: від’ємно означена квадратична форма є угнутою, а додат­но означена — опуклою.

Розглянемо випадок від’ємно означеної квадратичної форми, що входить у цільову функцію задачі квадратичного програмування.

max , (8.42)

; (8.43)

. (8.44)

Оскільки цільова функція задачі є опуклою, а обмеження — лінійні, тобто визначають опуклу множину допустимих розв’язків, то ця задача належить до задач опуклого програмування, для яких справджується твердження, що будь-який локальний максимум є і глобальним. Отже, використовуючи умови теореми Куна — Таккера для задачі (8.42)—(8.44), отримаємо необхідні та достатні умови оптимальності плану у вигляді такої теореми.

Теорема 8.6. Вектор Х^* є оптимальним розв’язком задачі квадратичного програмування тоді, і тільки тоді, коли існують такі m-вимірні вектори і n-вимірний вектор , що виконуються умови:

(І) , ; (8.45)

(ІІ) , ; (8.46)

(ІІІ) , ; (8.47)

(ІV) , . (8.48)

Доведення. Запишемо функцію Лагранжа для задачі квадратич­ного програмування (8.42)—(8.44):

+. (8.49)

Нехай — сідлова точка функції Лагранжа, тобто яка визначає оптимальний план задачі квадратичного програмування. Застосуємо теорему 8.4 до виразу (8.49). За теоремою для того, щоб точка визначала оптимальний план, необхідно і достатньо виконання умов (8.38)—(8.41):

для має виконуватись умова:

, , (8.50)

а також , (8.51)

а для має виконуватись умова:

, , (8.52)

а також . (8.53)

Візьмемо два вектори та , компоненти яких будуть введені як додаткові змінні в рівняння (8.50) та (8.52). Для цього виберемо , якщо і , якщо . Аналогічно виберемо , якщо і , якщо . Тепер додамо компоненти вектора у (8.50) і віднімемо компоненти век­тора від (8.52). Враховуючи правила вибору компонент векторів, матимемо для (8.50):

, .

Звідси: , тому для (8.51) маємо:

.

Аналогічно для другої групи обмежень:

, .

Звідки , тому .

Теорему доведено.

Наведену теорему можна використати для побудови ефективного методу розв’язування задач квадратичного програмування на основі алгоритму симплексного методу.

Умови (8.45)—(8.49) утворюють стосовно змінних систему (n + m) рівнянь з 2(n + m) невідомими.

Умови (8.47) та (8.48) означають, що змінні не можуть одночасно мати додатні значення, тобто входити в базис разом. Якщо деякі k компонент вектора додатні, то відповідні їм компоненти вектора V дорівнюють нулю і лише (n – k) компонент відмінні від нуля (додатні). Отже, разом будуть мати не більш ніж n додатних компонент. З аналогічних міркувань щодо рівності (8.48) випливає, що разом з буде n + m відмінних від нуля компонент, тобто це може бути базисний розв’язок системи, що утворена умовами (8.45) та (8.47). Для знаходження такого розв’язку можна застосувати симплексний метод.

Якщо зазначена система рівнянь має допустимий план (він буде єдиним), то оптимальний план відповідної задачі квадратич­ного програмування також існує.

Розв’язуємо систему рівнянь (8.45) і (8.47) симплексним методом. Як відомо, спочатку необхідно привести систему обмежень до канонічного виду введенням потрібної кількості додаткових та штучних змінних. Для зведення системи до канонічної форми та визначення початкового опорного плану вводимо штучні змінні у рівняння виду (8.45), які будуть базисними для першого опорного плану, а змінні — у групу рівнянь (8.47), які також дають базисні змінні для початкового плану. Потім для знаходження базисного розв’язку системи (8.45), (8.47) розв’язуємо симплексним методом таку задачу лінійного програмування:

max 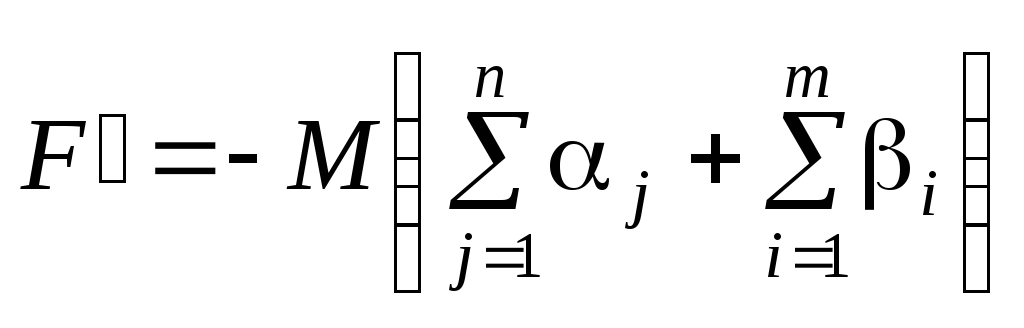(8.54)

за умов:

(8.55)

. (8.56)

Якщо в процесі розв’язування задачі (8.54)—(8.56) всі штучні змінні будуть виведені з базису і разом з цим для знайдених значень змінних виконуються умови (8.46), (8.48), то знайдений розв’язок є оптимальним планом задачі квадратичного програмування (8.42)—(8.44).

Розв’язати задачу квадратичного програмування:

за умов:

Розв’язання. Оскільки цільова функція виражена сумою лінійної функції та квадратичної форми , а система обмежень є лінійною, то маємо задачу квадратичного програмування.

Визначимо вид квадратичної форми , для чого відшукаємо корені характеристичного рівняння, що відповідає матриці, складеній з коефіцієнтів при змінних даної функції:

.

Характеристичним рівнянням для матриці С буде:

Оскільки обидва корені характеристичного рівняння від’ємні, то квадратична форма є від’ємно означеною, а отже, опуклою.

Запишемо функцію Лагранжа для цієї задачі:

.

Скористаємося теоремою 8.4. Необхідні умови існування екст­ремуму матимуть вигляд:

, причому ;

, причому ;

, причому,

де — координати сідлової точки.

Обмеження, що відповідають нерівностям, запишемо у вигляді:

Вводимо додаткові змінні для зведення нерівностей до рівнянь:

Для зведення задачі до канонічної форми помножимо кожне рівняння на (–1):

Очевидно, що в даному разі штучні змінні необхідно вводити в перші два рівняння. У третьому рівнянні базисною змінною буде . Маємо таку задачу лінійного програмування:

,

.

Розв’язавши її симплексним методом, отримаємо:

Необхідно перевірити виконання умов:

;

;

.

Всі умови виконуються, отже, є сідловою точкою функції Лагранжа для задачі квадратичного програмування, а — оптимальним планом задачі, для якого значення функціонала дорівнює:

.