
Научные стремления 2012-1
.pdf
УДК 519.65
Худяков А. П.
ИНТЕРПОЛЯЦИОННЫЕ МНОГОЧЛЕНЫ ЭРМИТА–БИРКХОФА ПО СИСТЕМЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
Белорусский государственный университет, Минск
Интерполяционная задача Эрмита–Биркхофа для случая функций состоит в построении многочленов, для которых выполнялись бы условия совпадения значений многочлена и его производных некоторых фиксированных порядков во всех или отдельных узлах с соответствующими значениями интерполируемой функции и еѐ производных. Эта задача с пропусками порядков производных в отличие от задачи эрмитова типа не всегда разрешима [1–3].
Вболее общей постановке интерполяционной задачи Эрмита–Биркхофа условия совпадения в отдельных узлах производных заменяются на условия совпадения заданного дифференциального или некоторого другого вида оператора. В случае алгебраических многочленов интерполяционные формулы такого типа получены в [4–5].
Данное направление в теории аппроксимации функций еще мало изучено, поэтому в силу широкого применения теории интерполирования на практике, построение подобных многочленов является актуальной проблемой.
Вданной работе рассматривается обобщенная интерполяционная задача Эрмита–Биркхофа. Построены новые интерполяционные многочлены относительно двух видов рациональных функций, и соответственно, для двух видов линейных дифференциальных операторов.
|
Пусть в |
узлах t0 |
t1 tn |
заданы значения |
f (ti) |
функции |
f (t). |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кроме этого, в одном из узлов t j известно значение оператора |
Ln 1( f ;t j ) , где |
|||||||||||||
|
является дифференциальным оператором вида |
|
|
|
|
|||||||||
Ln 1 |
|
|
|
|
||||||||||
|
|
f (t) |
d |
n 1 |
|
|
q |
(t) (t c )(t c ) (t c ). |
|
|
||||
|
L |
|
|
|
[q (t) f (t)], |
|
|
|||||||
|
|
|
|
|
|
|
||||||||
|
n 1 |
|
dtn 1 |
|
n |
n |
0 |
1 |
n |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
Рассмотрим рациональные функции k (t) вида |
|
|
|
|
|||||||||
|
|
k (t) |
|
1 |
|
t ck 0, |
k 0,1,...,n 1; |
t R . |
|
(1) |
||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
t |
ck |
|
|
|
~ |
|
|
|||
|
В данном случае задача состоит в построении полинома |
степени |
||||||||||||
|
Ln 1(t) |
|||||||||||||
n 1 на базе рациональных функций (1), для которого выполнялись бы
следующие условия: |
|
|
|
|
~ |
|
|
~ |
|
|
|
|
|||
i 0, n ; |
|
||||||
Ln 1(ti ) f (ti ) |
Ln 1 Ln 1;t j Ln 1( f ;t j ). |
(2) |
|||||
Положим n (t) (t t0 )(t t1) (t tn ),
n (cn 1 t0 )(cn 1 t1) (cn 1 tn ).
Те о р е м а 1. Многочлен
401

|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
~ |
|
|
|
|
|
n |
(t)(t |
j |
)n 2 L |
|
( f ;t |
j |
) |
|
|
|
|
||||||||
|
L |
|
(t) L (t) |
|
|
|
|
|
n 1 |
|
|
|
n 1 |
|
|
, |
|
|
(3) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
n 1 |
|
n |
|
|
|
|
|
qn 1(t)(n 1)! n |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
n |
n (t)qn (tk ) |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Ln (t) |
|
|
|
f (tk ), |
|
|
|
|
|
(4) |
|||||||||||||
|
|
|
|
q (t) |
|
) |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
k 0 |
|
(t |
k |
)(t t |
k |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
степени n 1 удовлетворяет условиям (2). |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Получено |
явное |
|
представление |
остаточного |
члена |
для |
||||||||||||||||||||
интерполяционного полинома (3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Л е м м а |
1. |
Пусть |
(n 1) -непрерывно-дифференцируемая на отрезке |
|||||||||||||||||||||||
[a,b] функция |
f (t) |
имеет на этом промежутке n 2 нулей. Тогда на отрезке |
||||||||||||||||||||||||
[a,b] найдется такая точка , |
что |
|
функция |
|
|
|
|
|
входящая |
в |
||||||||||||||||
|
Ln 1( f ;t), |
|||||||||||||||||||||||||
интерполяционную формулу (3), обращается в нуль в точке . |
|
|
|
|||||||||||||||||||||||
Т е о р е м а |
2. Если функция |
f (t) |
дифференцируема |
n 2 |
раз |
на |
||||||||||||||||||||
отрезке [a,b], то остаточный член формулы (3) имеет вид
~ |
(t) |
Rn 1(t) f (t) Ln 1 |
|
где , [a;b]. |
|
n (t) |
|
|
|
|
L |
( f ; ) |
|||
|
||||
q (t)(n 1)! |
n 1 |
|
||
n |
|
|
|
|
|
|
c |
|
|
|
) |
|
(t |
j |
)n 2 L |
( f ;t |
j |
|||
|
n 1 |
n 1 |
|
|
|
||
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
(t cn 1) n |
|
|
|
|
|
|
|
|
|
|
|
||
(5)
Далее получена оценка погрешности формулы (3). Введем обозначения:
Bn (a c0 )(a c1) (a cn ), Mn 1 max |
|
|
|
|
|
|
|
|
|
|||||||||
|
Ln 1( f ; ). |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
[a,b] |
|
|
|
|
|
|
|
|
|
|
Т е о р е м а 3. Оценка погрешности формулы (3) для любого t [a,b] |
||||||||||||||||||
имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
(b a)n 1 M |
n 1 |
|
(t j cn 1)n 2 |
|
|
|||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
f (t) L |
(t) |
|
|
|
|
1 |
|
|
|
|
. |
|
(6) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
n 1 |
|
|
|
Bn (n 1)! |
|
|
(a cn 1) n |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
П р и м е р 1. Пусть |
f (t) et 2 . Рассмотрим частные случаи формулы (3) |
|||||||||||||||||
при n 1, 2,3, |
соответственно, |
с узлами tk |
k, k |
|
; n 1, 2,3 . |
Точность |
||||||||||||
0, n |
||||||||||||||||||
приближения |
этой функции многочленами |
~ |
|
~ |
и |
~ |
||||||||||||
L2 (t), |
L3 (t) |
L4 (t) |
||||||||||||||||
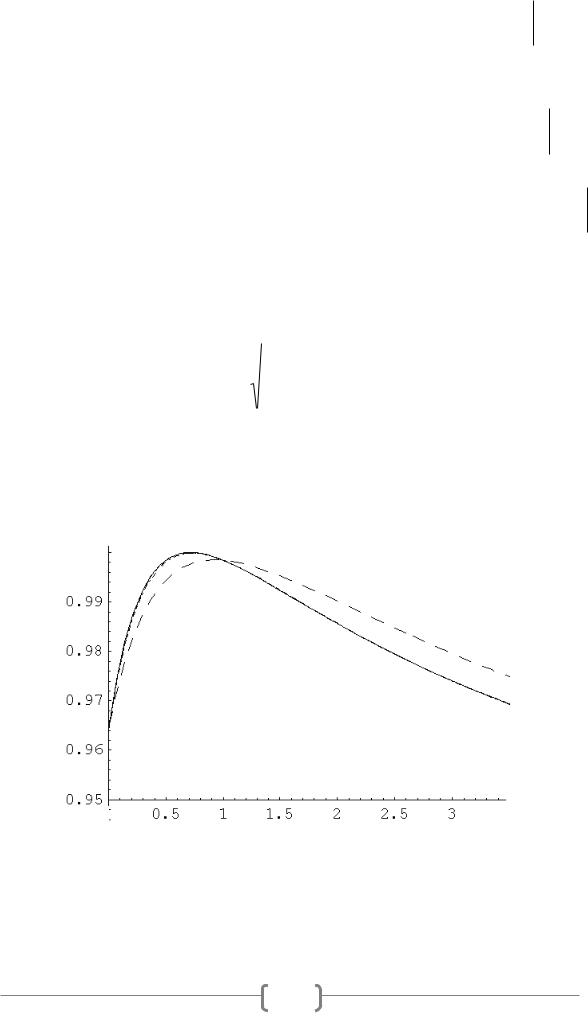
иллюстрируется на графике (рисунок 1). Сплошной линией дается график
штрих-пунктирной – |
~ |
(t), пунктирной – |
L3 |
этой функции, штриховой – ~
~
L2 (t),
L4 (t).
402

1.6 |
y(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
|
1.4 |
|
|
|
|
|
|
|
1.3 |
|
|
|
|
|
|
|
1.2 |
|
|
|
|
|
|
|
1.1 |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 1. |
|
|
|
|
|
|
|
|
|
|
|||||||||
Интерполяционный |
многочлен |
~ |
|
|
достаточно точно описывает |
||||||||||||||||||||||||||||
L4 |
(t) |
|
|||||||||||||||||||||||||||||||
поведение функции |
|
f (t) на отрезке [0,3]. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Рассмотрим еще одну задачу интерполирования на базе рациональных |
|||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функций k (t) |
|
|
|
|
k |
0, n . |
|
|
|
Построен |
|
интерполяционный |
полином |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
(t |
|
c)k |
|
|
|
|
|
||||||||||||||||||||||||||
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ln 1(t) степени n 1, для которого выполнялись бы условия |
|
|
|||||||||||||||||||||||||||||||
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
i 0, n ; |
|
|
|
|
|
|
|
|
|||||||||||||||
|
Ln 1(ti ) f (ti ) |
|
|
Ln 1 Ln 1;t j Ln 1( f ;t j ), |
(7) |
||||||||||||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
n 1 |
|
c) |
n |
f (t)] |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
L |
|
|
f (t) |
|
[(t |
|
|
, |
|
|
|
|
|
(8) |
|||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
dtn 1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Т е о р е м а 4. Многочлен степени n 1 относительно этой системы |
|||||||||||||||||||||||||||||||||
функций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
n |
(t)(t |
j |
c)n 2 L |
|
( f ;t |
j |
) |
|
|
|
|||||||||
|
|
|
L |
|
(t) L (t) |
|
|
|
|
|
|
|
|
|
n 1 |
|
|
, |
|
(9) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(t c)n 1(n 1)!с |
|
|
|
|||||||||||||||||||
|
|
|
|
n 1 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ln (t) |
1 |
|
|
n (t)(tk c) |
|
|
|
|
f (tk ), cn (c t0 )(c t1) (c tn ), |
||||||||||||||||||||||||
|
|
|
n |
) |
|
||||||||||||||||||||||||||||
|
(t c) |
|
k 0 |
(t t |
k |
) (t |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
степени n 1 удовлетворяет условиям (7). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Получено также представление остаточного члена и оценка |
|||||||||||||||||||||||||||||||||
погрешности для полинома (9). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Л е м м а |
2. |
Пусть |
(n 1) -непрерывно-дифференцируемая на отрезке |
||||||||||||||||||||||||||||||
[a,b] функция |
f (t) |
имеет на этом промежутке n 2 нулей. Тогда на отрезке |
|||||||||||||||||||||||||||||||
[a,b] найдется такая точка , что функция |
|
|
|
|
в формуле (9) |
||||||||||||||||||||||||||||
Ln 1( f ;t) |
|||||||||||||||||||||||||||||||||
обращается в нуль в точке . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Т е о р е м а |
5. |
Если |
функция |
|
|
f (t) |
дифференцируема |
n 2 |
раза на |
||||||||||||||||||||||||
отрезке [a,b], |
то остаточный член формулы (9) имеет вид |
|
|
||||||||||||||||||||||||||||||
403
|
|
|
|
n |
(t)( t |
j |
) |
|
d |
|
|
|
|
R |
(t) f (t) L |
(t) |
|
|
|
|
(t c)n 2 L |
( f ;t) |
, |
(10) |
|||
|
|
|
|
|
|
|
|||||||
n 1 |
n 1 |
|
(n 1)!(t c)n 1cn |
|
dt |
n 1 |
|
|
|
||||
|
|
|
|
|
t |
|
|
||||||
где , [a;b]. |
|
|
|
|
|
|
|
|
|||
Преобразуем правую часть (10): |
|
|
|||||||||
|
|
|
n |
(t)( t |
j |
)( c)n 1 |
|
|
|
|
|
R |
(t) |
|
|
|
(n 2)L |
( f ; ) |
|||||
|
|
|
|
|
|||||||
|
|
|
c)n 1cn |
||||||||
n 1 |
|
|
(n 1)!(t |
|
|
n 1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Введем обозначения: Mn 1 |
|
|
|
|
|
||||||
|
|
|
|||||||||
max |
Ln 1( f ;t) |
, |
|||||||||
|
|
|
|
|
|
|
|
t [a,b] |
|
|
|
|
|
|
d |
|
|
|
|
||||
( c) |
|
L |
( f ;t) |
. |
|
||||||
|
|
||||||||||
|
|
|
dt |
n 1 |
|
|
|
||||
|
|
|
|
|
|
|
|
t |
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
(11) |
|||
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
B |
max |
|
L |
( f ;t) |
. |
||||||
|
|||||||||||
n 1 |
|
t [a,b] |
dt |
n 1 |
|
|
|
||||
|
|
|
|
|
|
||||||
Т е о р е м а |
6. Оценка погрешности формулы (9) для любого t [a,b] |
||||||||||||||||||||
имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
(b a)n 2 (b с)n 1 |
(n 2)M n 1 (b c)Bn 1 . |
|
||||||||||||
|
|
|
|
|
|||||||||||||||||
|
f (t) Ln 1(t) |
|
|
|
|
(12) |
|||||||||||||||
|
|
(n 1)!(a с)n 1c |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
П р и м е р |
|
2. |
Пусть |
f (t) |
|
sin e 2t 3 . |
Рассмотрим формулу (9) при |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
; n 1, 2,3 . |
|
|
|||
n 1, 2,3, соответственно, |
с узлами |
|
k, |
|
Точность |
||||||||||||||||
tk |
0, n |
||||||||||||||||||||
приближения |
этой функции |
многочленами |
~ |
|
~ |
и |
~ |
||||||||||||||
L2 (t), |
L3 (t) |
L4 (t) |
|||||||||||||||||||
иллюстрируется на графике (рисунок 2). |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Сплошной |
линией |
изобразим |
интерполируемую |
функцию |
f (t), |
||||||||||||||||
~ |
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
~ |
|
|
|
штриховой – L2 |
(t), |
штрих-пунктирной – L3 |
(t), пунктирной – L4 (t). |
|
|
||||||||||||||||
y(t)
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
Рисунок |
2. |
|
Как и |
на |
предыдущих |
рисунках |
этой главы, |
интерполяционные |
|||
многочлены |
~ |
(t) и |
~ |
|
фактически совпадают с |
интерполируемой |
||
L3 |
L4 |
(t) |
||||||
функцией.
404

Литературные источники
1.Ж и д к о в Н. П. Линейные аппроксимации функционалов. М., 1977.
2. И б р а г и м о в И. И. Методы интерполяции функций и их некоторые применения. М., 1971.
3.Т у р е ц к и й А. Х. Теория интерполирования в задачах. Мн., 1968.
4.Я н о в и ч Л. А., И г н а т е н к о М. В. // Докл. НАН Беларуси. 2009. Т. 53, № 5. С.
15 – 21.
5.Я н о в и ч Л. А., И г н а т е н к о М. В. // Актуальные проблемы анализа: Сб. науч. тр. Гродно: ГрГУ, 2009. С. 198 – 215.
6. |
М а к а р о в |
В. Л., Х л о б ы с т о в В. В., Я н о в и ч Л. А. Интерполирование |
операторов. Киев, 2000. |
||
7. |
Х у д я к о в |
А. П. // Весці НАН Беларусі. Сер. фіз.-мат. навук. 2010. № 4. С. 29– |
36. |
|
|
8.Х а у с х о л д е р А. С. Основы численного анализа. М., 1956.
9.Г у л о И. Н., Я н о в и ч Л. А. // Докл. НАН Беларуси. 2010. Т. 54, № 3. С. 14 – 19.
10.Л и т в и н О. М., Р в а ч о в В. Л. Класична формула Тейлора її узагальнення та застосування. Киів, 1973.
A. P. Hudyakov
HERMITE–BIRKHOFF’S TYPE INTERPOLATION POLYNOMIALS ON
SYSTEM OF RATIONAL FUNCTIONS
Belarusian state university, Minsk
Summary
In this work Hermite-Birkhoff's generalized interpolation problem is considered. New interpolation polynomials with respect to two types of rational functions, and respectively, for special types of linear differential operators are constructed.
405

УДК 239.2
Чернолевская Е.А., Дорошенко И.Ю., Борздая Т.В.
ТЕОРЕТИЧЕСКОЕ И ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ КЛАСТЕРОВ МЕТАНОЛА В ГАЗОВОЙ ФАЗЕ И АРГОНОВЫХ МАТРИЦАХ.
Киевский национальный университет имени Тараса Шевченко, Киев, Украина
Использование методов спектроскопии в физике делает возможным решение многих задач прикладного характера с одной стороны, а с другой – позволяет исследовать структуру многоатомных молекул, природу и характер межмолекулярных взаимодействий, строение и динамику внутренней структуры различных соединений [1]. В данной работе объектом наших исследований был метанол в аргоновой матрице и в газовой фазе.
Спирты, также как и вода, являются весьма распространенными веществами, потому исследование их структуры весьма актуально как с точки зрения фундаментальной науки [2,3], так и, например, для промышленных целей. Актуальность исследования именно метанола обусловлена его широким применением в промышленности, качестве топлива, в двигателях внутреннего сгорания как источник энергии в специфических топливных элементах. С точки зрения теоретических исследований методами квантовохимического моделирования метанол интересен тем, что является простейшим спиртом (первым в гомологическом ряду одноатомных спиртов), его молекула состоит из достаточно небольшого количества атомов, что позволяет сократить время и компьютерные мощности, необходимые для теоретических расчетов [4,5].
Спирты – это типичный пример частично упорядоченных жидкостей. Потому целью наших исследований было изучение структуры метанола в различных фазовых состояниях, а также сравнение экспериментально полученных ИК-спектров с результатами компьютерного моделирования исследуемых структур с использованием метода молекулярной динамики. В данной работе представлены результаты исследований метанола, являющегося веществом, которое принадлежит к классу соединений с водородной связью. Этот факт позволяет прийти к умозаключению, что за счет наличия водородной связи в подобного рода соединениях существует возможность образования молекулярных ассоциатов, называемых кластерами, с различным числом молекул в кластере. Именно наличие гидроксильной группы в молекулах спиртов приводит к образованию водородной связи, что впоследствии главным образом и определяет структуру этих соединений. Именно благодаря наличию водородной связи возможно наблюдать такое специфическое межмолекулярное взаимодействие, энергия которого значительно превышает энергии обычных ван-дер-ваальсовских взаимодействий и лишь на порядок меньше сильных химических связей. Это и обеспечивает ассоциацию отдельных молекул в группы и образование
406
молекулярных кластеров, что впоследствии сильно влияет на свойства |
|||||||
исследуемых веществ, как следствие изменения их структурного строения. |
|||||||
Спирты являются одними из простейших органических соединений, |
|||||||
способных к образованию водородно-связанных агрегатов. Кроме того, это |
|||||||
весьма адекватные |
модели |
для |
описания |
динамики образования |
агрегатов |
||
(многомолекулярных кластеров). |
|
|
|
|
|
||
В данной работе представлено предварительное сравнение |
|||||||
экспериментально полученных ИК спектров метанола в матрице аргона в |
|||||||
диапазоне температур от 10 до 50 К с результатами, полученными с |
|||||||
использованием компьютерного моделирования ab initio методом Car- |
|||||||
Parrinelo molecular dynamics (CPMD) и статические расчеты квантовой химии. |
|||||||
Наши результаты ясно показывают хорошую корреляцию теоретических |
|||||||
расчетов для кластеров, состоящих из небольшого количества молекул, с |
|||||||
экспериментальными данными для метанола в аргоновой матрице при |
|||||||
соответствующих температурах. |
|
|
|
50K |
|
||
|
|
|
|
|
|
40K |
|
|
|
|
|
|
|
30K |
|
|
|
|
|
|
|
MD 50K |
|
3100 |
3200 |
3300 |
3400 |
3500 |
3600 |
3700 |
3800 |
|
|
|
|
-1 |
|
|
|
|
|
|
волновое число, cм |
|
|
|
|
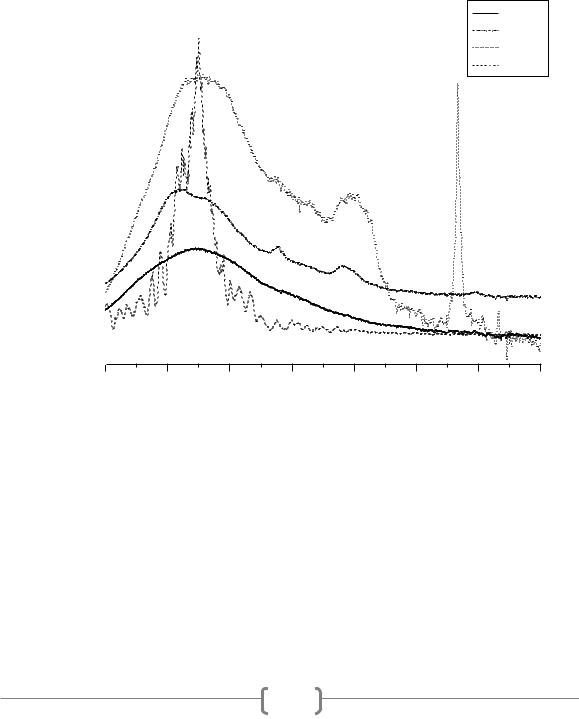
Рисунок 1. Сравнение спектров MД моделирования с экспериментальными ИК спектрами метанола в аргоновой матрице при различных температурах
В данной работе представлены первые результаты DFT-MД исследования метанола. Жидкий метанол был смоделирован следующим образом: размер бокса выбирался из соображений его соизмеримости с размером полости в аргоновой матрице – 15 Å. В этот бокс помещались четыре молекулы метанола. В DFT-MД моделировании были использованы метод Кар-Паринелло, DFT функционал B3LYP, псевдопотенциал и
407
плосковолновой базисный набор. Временной шаг в МД вычислениях составил 0,2 фс при длине временной траектории 100-200 пс.
|
|
|
|
50K |
|
|
|
|
|
40K |
|
|
|
|
|
25K |
|
. |
|
|
|
10K |
|
|
|
|
MD 50K |
|
|
|
|
|
|
|
|
1020 |
1030 |
1040 |
-1 |
1050 |
1060 |
|
|
волновое число, cм |
|
|
|
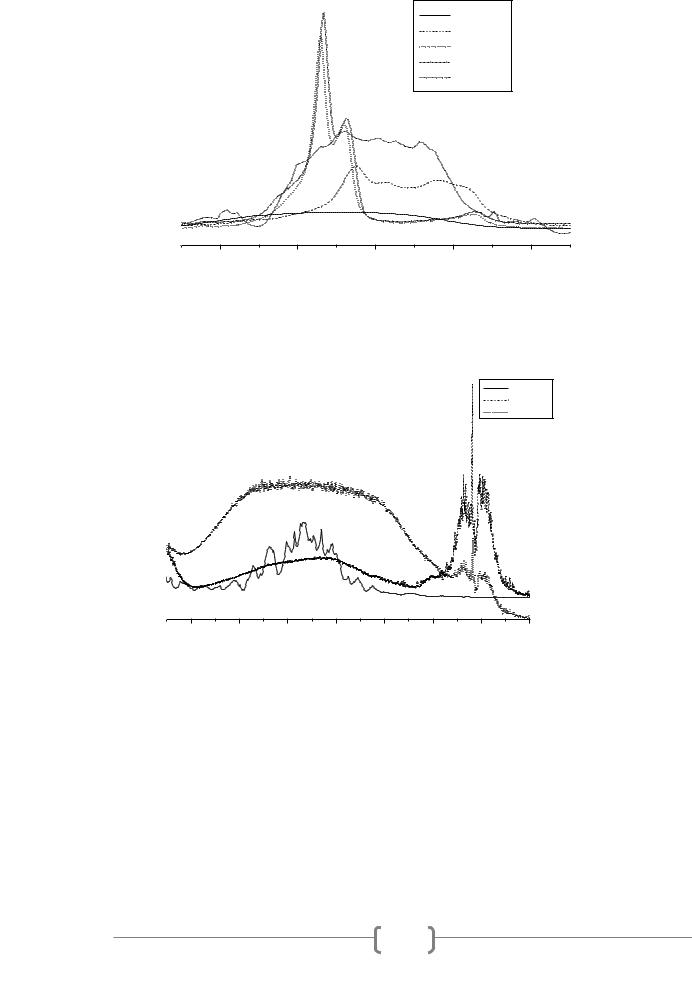
Рисунок 2. Сравнение спектров MД моделирования с экспериментальными ИК спектрами метанола в аргоновой матрице, полученные при различных температурах.
|
|
|
|
|
|
|
ÌÄ 200K |
|
|
|
|
|
|
|
20C |
|
|
|
|
|
|
|
20C |
3100 |
3200 |
3300 |
3400 |
3500-1 |
3600 |
3700 |
3800 |
|
|
|
волновое число, cм |
|
|
|
|
Рисунок 3. Сравнение спектров MД моделирования с экспериментальными ИК спектрами метанола в газовой фазе полученными при 20 ° С.
Сравнительный анализ экспериментально полученных ИК спектров со спектрами, полученными с использованием компьютерного моделирования показал, что результаты моделирования с использованием молекулярной динамики хорошо согласуются с экспериментальными данными. Таким образом, мы можем прийти к заключению об адекватности использования MД моделирования данных структур и отметить что данный подход позволяет продвинуться в изучении структурных свойств жидкого метанола.
408

Рассчитанные спектры метанола хорошо коррелируют с экспериментом и дают представление о реальной структуре кластеров метанола при соответствующей температуре.
Литературные источники
1.Дорошенко И.Ю., Погорелов В.Е, Пицевич Г.А., Шаблинскас В. Кластерная структура жидких спиртов: исследование методами колебательной спектроскопии. –
Lambert Academic Publishers, 2012. – 279 c.
2.Sarkar S., Joarder R.N., J. Chem. Phys., 99 (1993) 2032.
3.Buck U., Huisken F., Chem. Rev. – 100 (2002) 3863.
4.Boyd S.L., Boyd R.J., J. Chem. Theory Comput., 3 (2007) 54.
5.Doroshenko І., Lizengevych О., Pogorelov V., Savransky L., Ukr. J. Phys. 49 (2004) 540.
Chernolevskaya Ye.A., Doroshenko I.Yu., Borzda T.V.
THEORETICAL AND EXPERIMENTAL STADY OF METHANOL CLUSTERS:INFRARED
SPECTRA IN THE GAS PHASE AND ARGON MATRIX
Kyiv National Taras Shevchenko University, Kiev, Ukraine
Summary
Now the objects of our investigation is methanol in argon matrix and gas phase methanol. This alcohol belong to the class of substances with hydrogen bond, so there is a possibility to form molecular associations-called cluster with different number of molecules .
In our work we present the preliminary comparison of the in experimentally obtained IR spectra of the methanol in argon matrix in the temperature range 10 to 50 K with the results obtained from the computer simulation using the ab initio Car-Parrinelo molecular dynamics(CPMD) and static quantum chemistry calculations.
Our results clearly show that small cluster models well correlate with experimental data in argon matrix at the corresponding temperatures.
409

СЕРИЯ «ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ»
УДК 004.932.4
Chekhovich A.V. 1
Algorithm for increasing resolution of the video fragments
1 Belarusian State University of Informatics and Radioelectronics
Introduction
Super-Resolution (SR) are techniques that construct high-resolution (HR) images from several observed low-resolution (LR) images. This process has also been referred to in the literature as resolution enhancement (RE).
The image spatial resolution is limited by the imaging sensors of the imaging acquisition device. Lens blurs (associated with the sensor point spread function (PSF)), lens aberration effects, aperture distractions, and optical blurring due to motion are degradation parameters present in any image acquisition system.
Physical constraints limit image resolution quality in many imaging applications. These imaging systems yield aliased and undersampled images if their detector array is not sufficiently dense. This is particularly true for infrared imagers and some charge-coupled device (CCD) cameras.
Constructing imaging chips and optical components to capture very highresolution images is prohibitively expensive. SR techniques accept the image degradations and use signal processing to post-process the captured images, to trade off computational cost with the hardware cost.
A dynamic scene with continuous intensity distribution X (x, y) is seen to be warped at the camera lens because of the relative motion between the scene and camera. The images are blurred both by atmospheric turbulence and camera lens by continuous point spread functions Hatm(x, y) and Hcam (x, y) . Then, they will be
discretized at the CCD resulting in a digitized noisy frame Y (m, n)
Y (m, n) [Hcam (x, y)**F(Hatm(x, y)**X (x, y)] V[m, n] |
(1) |
The multiframe super-resolution problem was first addressed in [1], where they proposed a frequency domain approach, extended by others, such as [2]. Although the frequency domain methods are intuitively simple and computationally cheap, they are extremely sensitive to model errors [3], limiting their use. Also, by definition, only pure translational motion can be treated with such tools and even small deviations from translational motion significantly degrade performance.
Another popular class of methods solves the problem of resolution enhancement in the spatial domain. The spatial domain methods discussed so far are generally computationally expensive. The authors in [4] introduced a block circulant preconditioner for solving the Tikhonov regularized super-resolution problem formulated in [5] and addressed the calculation of regularization factor for the under-determined case by generalized cross validation in [6]. Later, a very fast super-resolution algorithm for pure translational motion and common space
410
