|
(2( ( |
k |
|
2)(1 |
k |
|
)( |
cos() |
|
sin()) (1 |
k |
)( |
sin() cos())) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2( |
k |
|
3)( ( |
k |
|
|
2)(1 |
k |
)( |
cos() |
sin()) (1 |
k |
)( sin() cos())) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
(( |
|
(4) k |
|
|
(2 |
|
|
|
) |
|
|
( |
|
|
2)(( (4) k |
|
|
|
|
(2 |
|
|
) )) cos() ( |
|
|
|
(2 |
|
) |
|
( |
|
2) |
|
|
|
|
|
|
k |
k |
|
|
k |
|
k |
k |
k |
k |
k |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(( |
|
|
k |
(2 |
k |
|
) |
) sin() ( |
|
(5) |
|
|
k |
|
(2 |
k |
) |
|
k |
(2 |
k |
) |
k |
)sin() |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
(4) |
|
|
k |
(2 |
k |
) |
|
|
|
|
|
|
k |
(2 |
k |
) |
|
k |
) cos())) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
( |
|
|
|
3)( ( |
|
|
|
2)( |
|
|
|
|
(2 |
|
|
) |
|
|
) cos() ( |
|
|
|
(2 |
|
|
) |
)sin()) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
k |
|
|
k |
k |
|
k |
k |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
k |
|
3)(( |
k |
|
|
2)( |
|
|
|
k |
|
(2 |
k |
) |
k |
|
) cos() ( |
|
k |
(2 |
k |
) |
|
)sin()) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
( |
|
|
|
3)( |
|
|
|
4)(( |
|
|
|
|
|
2)( |
|
|
|
(2 |
|
) |
|
|
|
|
) cos() ( |
|
|
|
|
(2 |
|
|
|
) )sin())r k 5 )r k 3 |
|
|
|
|
|
k |
|
k |
|
k |
|
|
|
k |
k |
|
k |
|
|
k |
|
k |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A3 |
|
|
2((( ( |
|
|
|
|
|
|
|
4)(a |
|
|
|
cos() a |
|
|
|
sin()) (a sin() a |
|
|
cos()))(1 |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
l |
|
kl |
|
kl |
|
|
m |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
k 0 l 0 |
m 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ( |
k |
|
l |
|
4)a |
kl |
cos() a |
|
|
sin())(1 |
m |
) |
) 2( |
k |
|
|
l |
|
m |
|
7)(( ( |
k |
|
l |
4)(a |
cos() |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
a |
kl |
|
sin()) (a sin() a |
|
cos()))(1 |
m |
) |
( ( |
k |
|
|
l |
4)a |
kl |
cos() a |
sin())(1 |
m |
) ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
m |
|
|
1 |
|
|
(( ( |
|
|
|
|
|
4)(a |
|
cos() a |
|
sin() a |
|
|
sin() a |
|
|
|
cos()) (a sin() a |
cos() a cos() |
|
|
|
|
k |
|
l |
|
|
|
|
|
kl |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
sin( )))( |
|
|
|
m |
(2 |
m |
) |
|
m |
) ( ( |
k |
|
|
|
|
|
|
4)(a |
|
|
cos( ) a |
kl |
sin( )) (a sin( ) a |
cos( ))) |
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
kl |
|
|
|
|
( |
|
|
m |
(2 |
m |
|
) |
) ( ( |
k |
|
|
4)(a |
kl |
cos( ) a |
kl |
sin( )) (a sin( ) a cos( )))( |
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
m |
|
|
|
|
m |
(2 |
m |
) |
) ( ( |
k |
4)a |
kl |
cos( ) a |
sin( ))( (4) m |
|
m |
(2 |
m |
|
) |
)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
( |
|
|
|
|
|
|
|
7)( ( |
|
|
|
|
|
4)a |
|
|
cos( ) a |
sin( ))( |
|
|
|
(2 |
|
|
) |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
m |
|
k |
|
|
kl |
m |
m |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
k |
|
|
m |
7)(( |
k |
|
|
4)a |
kl |
cos( ) a |
|
|
sin( ))( |
|
|
|
m |
(2 |
m |
) |
m |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
( |
|
|
|
|
|
|
|
7)( |
|
|
|
|
|
|
|
8)(( |
|
|
|
|
|
|
|
4)a |
|
|
|
|
cos( ) a |
|
sin( ))( |
|
|
|
|
(2 |
|
|
) |
|
))r k l m 7 |
0. |
|
k |
|
m |
|
k |
m |
|
k |
|
l |
|
|
kl |
|
|
|
m |
m |
m |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kl |
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Граничные условия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k ( k 1)( ( k 2) k cos k sin )r |
k 3 |
|
| |
|
0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 k )( ( k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) k cos k sin )r |
|
| 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 k )( ( k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) k |
|
cos k |
|
sin )r |
|
| 0 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Анализ |
|
|
результатов. |
|
|
|
|
|
Приведем |
|
|
|
|
графики |
|
|
отнесенных |
|
компонент |
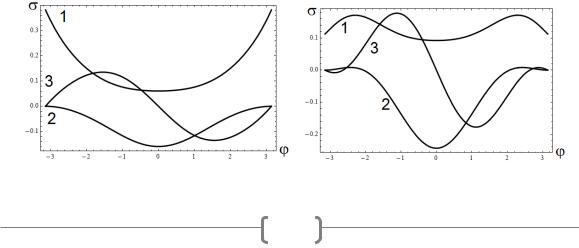
тензора напряжений в случае плоской деформации для нулевого приближения, в зависимости от угла для трещины общего вида.
в)
Рисунок 1. Угловое распределение компонент тензора напряжений в окрестности вершины страгивающейся трещины нормального отрыва в условиях плоского деформированного состояния (нулевое приближение) при различных значениях приращения длины ( l а)10 4 ;б)5 10 4 ;в)10 3 ). На графике введены следующие обозначения: линия 1 –
соответствует графику функции rr , линия 2 – графику функции и линия 3 –
графику функции r |
|
Расчеты проводились для |
меди со сдвиговым модулем |
G 0,442431 1011н / м2 и величиной |
A 1,3270501 10 5 |
, характеризующей |
|
2 |
|
нелинейность диаграммы деформирования материала.
Аналогично могут быть найдены и следующие члены разложения. Заметим, что вклады первого и второго приближения являются незначительными. Оценка погрешности производится в предположении асимптотической сходимости рядов решений.
Выводы. Построено нулевое приближение решения краевой упругопластической задачи в случае страгивания трещины нормального отрыва. Проанализированы поля напряжений и условия для параметра нагружения в окрестности вершины трещины.
|
|
Литературные источники |
1. |
Степанова Л.В. |
Математические методы механики разрушения. М: |
Физматлит, 2009. 336 с. |
|
2. |
|
Rahman, M. Elastic perfectly-plastic asymptotic |
mixed mode crack tip fields in plane stress/ M. Rahman, J.W. Hancock / Int. J. Solids and Structures. 2006. – V . 43. – P. 3692 – 3704.
3.Афанасьев E. Ф., Черепанов Г. П. Автомодельная задача динамической
теории упругости для щели с точечным источником. — Докл. АН СССР, 1970, т. 190, №
6.
4. Нифагин, В. А. Метод асимптотических разложений в теории упругопластических трещин / В.А. Нифагин, М.А. Бубич // Весцi НАН БЕЛАРУСI. Сер. Фiз.-мат. навук. –2011. – №4. – С. 60-66.
Hundzina M.A.
ASYMPTOTIC STRESS DURING BREAKAWAY CRACK NORMAL SEPARATION IN
THE THEORY OF PLASTICITY WITH HARDENING
Belarusian National Technical University, Minsk
Summary
We study the stress strain state of elastoplastic plane for subcritical growth at the top of a straight crack normal separation with relations of the theory of plasticity with hardening. Based variant of the method of asymptotic expansions, the problem is reduced to a recursive sequence of nonlinear boundary eigenvalue problems for a differential operator, which is solved numerically and analytically.
392

УДК 004.942
Карпович Д.С., Подобед М.Ю.
ПОВЫШЕНИЕ ТОЧНОСТИ ПОЗИЦИОНИРОВАНИЯ ЭЛЕКТРОМЕХАНИЧЕСКИХ СИСТЕМ ТРАНСПОРТИРОВКИ
ПРОДУКЦИИ
Белорусский государственный технологический университет, Минск
Задача определения координат электромеханической системы – наиболее актуальная в большинстве областей применения мобильных роботов. Точность позиционирования для систем транспортировки является наиважнейшим параметром, характеризующим качество работы всей системы автоматического управления. Поэтому к точности определения координат предъявляются особые требования.
Требование проверять текущую координату некоторого центра объекта диктуется необходимостью коррекции траектории, так как при длительной работе системы, даже достаточно точное позиционирование с использованием инкрементальных энкодеров в обратной связи и регуляторов положения система стремится к удалению от действительной траектории [1].
В данной работе рассматриваются способы уменьшения влияния шумов на точность позиционирования электромеханической системы с применение различных комбинаций из двух обратных связей, находятся средства измерения координаты.
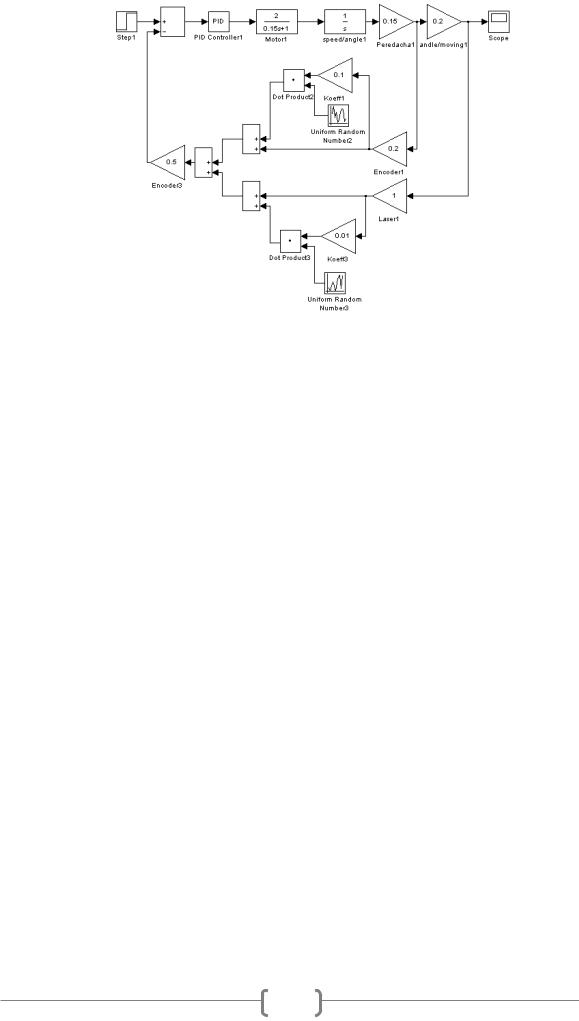
Вкачестве объекта исследования выступала электромеханическая система, предназначенная для выполнения различных транспортных операций связанных с позиционирование определенных предметов. Цель работы — разработка наиболее оптимальной системы управления положением электромеханической системы, обеспечивающей высокую точность позиционирования.
Моделируемая система будет состоять из электрического двигателя, механической передачи и двух датчиков перемещения в обратных связях. Регулятор будет осуществлять управление положением моделируемой системы.
Система позиционирования с один датчиком в обратной связи способна обеспечить точность определения координаты робота, лишь на определенных этапах своего существования. Со временем датчик подвержен влиянию различных факторов, под воздействием которых его точность уменьшается. Поэтому было решено, в рассматриваемой модели, использовать два датчика измерения положения системы различных по принципу работы. Структура модели приведена на рисунке 1.
Впервой обратной связи будет использован оптический абсолютный энкодер, считающийся очень надежным средством измерения положения. Для определения линейных и угловых перемещений в системах автоматического управления различного назначения широко используются два типа
оптических |
кодирующих |
устройств: |
шифраторы |
приращений |

(инкрементальные энкодеры) и программируемые шифраторы (абсолютные энкодеры). Для инкрементального энкодера необходим счетчик импульсов, обеспечивающий измерение относительного значения угла от точки отсчета. А поскольку счетчики импульсов обычно не сохраняют информацию при отключении питания, то и датчик теряет измеренное значение угла поворота
[2].
Рисунок 1. Структура модели
Основным достоинством абсолютных энкодеров является их способность выдавать измеряемое значение как непосредственно после включения, так и в процессе вращения вала или поступательного движения объекта контроля. Кроме того, этот вид датчиков устойчив к вибрациям, а если при повышенной скорости изменения угловой позиции вала кодированный сигнал не может быть сформирован, истинное значение угла будет зарегистрировано после постепенного уменьшения скорости.
Принцип действия оптических датчиков основан на идентификации угловой позиции вала путем оптоэлектронного считывания штрихового кода с градуированного диска, жестко закрепленного на валу датчика. В абсолютном энкодере на диске выполнены концентрические дорожки. Каждая дорожка соответствует определенной цифровой битовой комбинации, и на ней формируется уникальный код для конкретной позиции вала.
Вторая обратная связь реализует навигацию по опорному маяку. Для определения расстояния применен принцип измерения времени задержки между излучаемым сигналом и принятым. Такой же метод используется в РЛС. В качестве поля распространения было выбрано воздушное, то есть звуковое, так как скорость звука имеет величину порядка около 340 м/с, время задержки на минимально возможном расстоянии имеет величину порядка и может быть измерено с помощью таймеров контроллера [3].
В процессе работы были рассчитаны и смоделированы системы автоматического управления без весовых коэффициентов в обратных связях, с постоянными весовыми коэффициентами, с динамическими весовыми коэффициентами (с учетом математического ожидания и дисперсии сигналов в обратных связях.
Эффективность системы автоматического управления определяется более качественным позиционированием и способностью эффективно сглаживать шумы.
Рисунок 2. Структурная схема АСУ без учета весовых коэффициентов
В модели без учета весовых коэффициентов суммарный сигнал двух обратных связей представляет как усредненное значение двух равноценных сигналов. Для структурной схемы такой системы представленной на рисунке 2, значения математического ожидания значения выходной величины и дисперсии составили 1.0005 и 0.0078.
Предыдущая система без учета весовых коэффициентов была бы абсолютно справедлива, если бы в ветвях обратных связей стояли одинаковые датчики. Но так как в нашем случае в обратных связях расположены датчики с заведомо разными классами точности, то целесообразно учитывать весовые коэффициенты в каждом канале. Весовые коэффициенты принимались равными значению класса точности датчика, находящегося в соседней обратной связи.
Так же были промоделированы системы с динамически меняющимися динамическими коэффициентами, значения весовых коэффициентов которой менялось в зависимости от дисперсии (для первой системы) и математического ожидания (для второй системы) сигнала обратной связи противоположного канала. Математическое ожидание и дисперсия высчитывались для интервала времени равного 0,24 секунды и при этом интервал последовательно сдвигается на 0,024 секунды в режиме реального времени.
По результатам моделирования сведенным в таблицу 1 можно видеть, что среди систем со стационарными весовыми коэффициентами система с учетом весовых коэффициентов имеет дисперсию равную 0.0018, что ближе к идеальному значению 0, чем у системы без учета весовых коэффициентов 0.0078. Если рассматривать системы с динамически меняющимися весовыми коэффициентами то, система в которой весовые коэффициенты в режиме реального времени зависят от математического ожидания, выглядит
395

предпочтительней, чем система с коэффициентами, зависящими от дисперсии сигнала. В первом случае математическое ожидание выходной величины составляет 0.0077, а во втором в два раза больше, что соответствует 0.0144.
Таблица 1 — Статистически данные выходного сигнала, моделируемых систем
Параметр выходного сигнала |
математическое |
дисперсия |
ожидание |
|
|
|
|
СУ со стационарными |
с учетом весовых |
1.0009 |
0.0018 |
коэффициентами |
коэффициентов |
|
|
|
без учета весовых |
1.0005 |
0.0078 |
|
коэффициентов |
|
|
СУ с динамически |
дисперсия |
0.9987 |
0.0144 |
изменяющимися весовыми |
математическое |
1.0004 |
0.0077 |
коэффициентами |
ожидание |
|
|
Литературные источники
1."Разработка роботов" [Электронный ресурс] / Режим доступа: http://robotdevelop.org/archives/484
2.Фарзане, Н. Г. Технологические измерения и приборы / Н. Г. Фарзане, Л. В. Илясов, А. Ю. Азим-заде. — М.: Высшая школа, 1989. — 456 с.
3.Информационно электронный портал ―RadioRadar‖ [Электронный ресурс] /
Режим доступа: http://www.radioradar.net/articles/scientific_technical/ /encoder.html
Karpovich D.S., Podobed M. Y.
IMPROVING ACCURACY OF POSITIONING ELECTROMECHANICAL SYSTEMS PRODUCT TRANSPORT
Belarusian State Technological University, Minsk
Summary
In this study optimal system controlling the position of the electromechanical system, which provides high accuracy. Was designed and simulated automatic control without weight coefficients in the feedback, with constant weights, with dynamic weights. The effectiveness of the automatic control system is defined more quality positioning and the ability to effectively smooth out the noise.
УДК 621.372(075.8)+004.92(075.8)
Макруш С.В.
КРАТКАЯ ИСТОРИЯ, НЕКОТОРЫЕ СВОЙСТВА И ПРИЛОЖЕНИЯ ВЕЙВЛЕТ-АНАЛИЗА
Белорусский государственный университет, Минск
Вейвлет-технологии начали серьезно развиваться в 80–90 годы прошлого века, хотя первый тип вейвлета был описан еще в 1909 году Хааром. Многие типы и семейства вейвлетов были названы именами ученых, которые внесли огромный вклад в разработку теоретических основ вейвлетов: Мейер, Добеши, Маллат и другие.
Вейвлет анализ предлагает метод выбора окна переменного размера. Он позволяет использовать большие временные интервалы, где нужна более точная информация о низкой частоте, и более короткие области, когда нужна информация о высокой частоте.
В качестве средства анализа физических процессов вейвлет-функции имеют ряд замечательных свойств.
Преобразование Фурье, которое является одним из основных средств такого анализа, не обладает свойством локализации во времени.
Дельта-функция Дирака представляет собой функционал, ставящий в соответствие некой функции ее значение в данной точке. Такое преобразование абсолютно локализовано во времени, но при этом полностью теряется информация о частоте процесса. В этой ситуации сталкиваемся с проявлением закона типа квантового соотношения неопределенности, то есть с невозможностью одновременно определить мгновенную частоту процесса и его значение в данный момент времени. Попытка уточнить один из этих параметров немедленно приводит к ухудшению наших знаний о другом параметре.[1]
Вейвлет-анализ по сути представляет собой семейство функций, реализующих различные варианты соотношения неопределенности и предоставляющих исследователю возможность гибкого выбора между ними. Фурье-анализ и его модификации (дискретное косинусное преобразование и другие) такими свойствами не обладают.
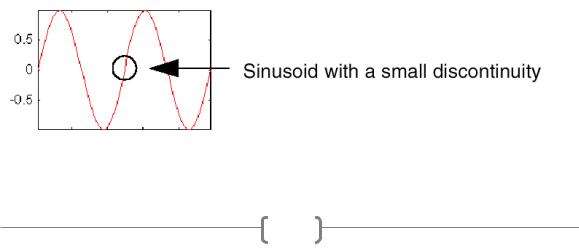
Одним главным преимуществом, которое предоставляет вейвлет, является возможность представлять локальный анализ, то есть анализировать локализованную область в большом сигнале:

График коэффициентов Фурье этого сигнала не показывает ничего особенно интересного: плоский спектр с двумя пиками, представляющими одну частоту. Однако график вейвлет коэффициентов ясно показывает точное расположение во времени рассмотренного выше разрыва:
Вейвлет-анализ способен выявить следующие особенности данных, которые упускают другие методы анализа сигналов: точки разрыва, резкие нелинейности в высших гармониках и самоподобие.
Большинство ограничений, накладываемых на вейвлет, связано с необходимостью иметь обратное преобразование. Рассмотрим основные ограничения:
Локализация. Вейвлет-преобразование использует базисную функцию, локализованную в пространстве времен и частот. Функции, не стремящиеся к нулю за пределами некоторой ограниченной окрестности, не могут являться вейвлетами.
Ограниченность.
t 2 dt . .
Практическая оценка ограниченности и локализации может быть записана в виде неравенств
|
|
|
|
const |
|
|
|
|
|
|
const |
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
. |
|
|
1 |
|
t |
|
n |
|
1 |
|
0 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число n должно быть возможно большим, 0 – доминантная частота вейвлета.
Нулевое среднее. Для ограниченности нормировочной константы обратного преобразования вейвлет должен удовлетворять условию равенства нулю нулевого момента (среднего по времени)
t dt 0.
Часто для практических приложений оказывается необходимым, чтобы нулю были равны не только нулевой, но и первые m моментов вейвлета:
t tmdt 0.
Такой вейвлет называется вейвлетом порядка m. Вейвлеты высокого порядка, обладающие большим количеством нулевых моментов, позволяют освободиться от влияния регулярных (полиномиальных) составляющих исследуемого процесса и сосредоточить внимание на анализе мелкомасштабных флуктуаций и особенностей высокого порядка.
Автомодельность базиса. Самоподобие базиса вейвлет-преобразования является его характерным признаком. Действительно, все функции данного семейства имеют одинаковое количество нулей, поскольку получены из базисного вейвлета с помощью системы преобразований подобия. Это облегчает применение вейвлет-преобразования для анализа фрактальных сигналов.[2]
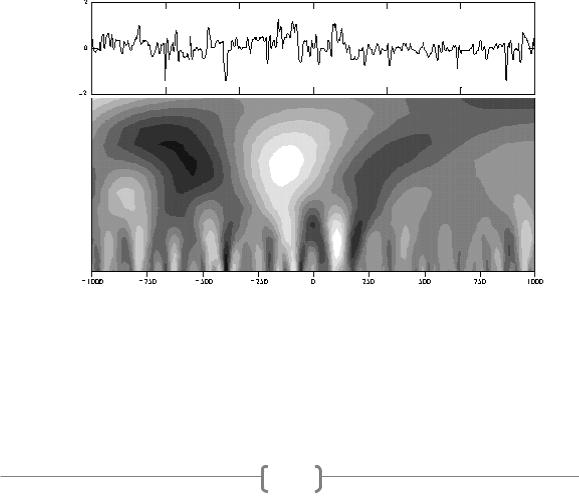
В отличие от преобразования Фурье, результатом вейвлет преобразования функции одной переменной является функция двух переменных. Она определяет двумерную поверхность в пространстве двух переменных a,b , соответствующих временному масштабу и временной локализации. Вид этой поверхности определяет эволюцию во времени спектральных компонент различного масштаба и называется частотновременным спектром. Эта поверхность изображается на рисунках, как правило, в виде изолиний или, условными цветами. Для расширения диапазона масштабов, представляемых на графике, применяется логарифмическая шкала.[3] Пример вейвлет-диаграммы реального физического процесса приведен на рисунке.
Временной ход допплеровского сдвига частоты и его вейвлет-спектр.
Здесь изображен типичный временной ход допплеровского сдвига частоты проходящего через ионосферу сигнала и его вейвлет-спектр. Хорошо заметно наличие в спектре сигнала высокочастотной компоненты с периодом порядка минут (мелкомасштабные чередующиеся области экстремумов в верхней части рисунка). Эти возмущения, по всей видимости, обусловлены

турбулентными пульсациями в ионосферной плазме. Встречающиеся в картине коэффициентов ветвления линий уровня говорят о фрактальной природе возмущений.
На таком графике можно легко проследить влияние каждого конкретного события на процессы различных временных масштабов, содержащиеся в исследуемом явлении.[4]
Список приложений вейвлетов чрезвычайно широк, причем области их применения не ограничиваются цифровой обработкой сигналов, но охватывают также физическое моделирование, численные методы и другие области.
Вероятно, такой интерес к вейвлетам вызван двумя факторами, вопервых, они сделали то, что долгое время не удавалось никому – предоставить альтернативу спектральному анализу и предоставить качественный инструмент анализа нестационарных сигналов, во-вторых, они представляют сигнал в пространственно-временной области, что существенно проще для понимания человеком.
Литературные источники
1.Дремин, И.М. Вейвлеты и их использование / И.М. Дремин, О.В. Иванов, В.А. Нечитайло // Успехи физических наук. – 2001.
2.Илюшин, Я.А. Теория и применение вейвлет-анализа / Я.А. Илюшин // 2001.
3.Астафьева Н.М., Вейвлет-анализ: основы теории и примеры применения / Астафьева Н.М. // Успехи физических наук – 1996.
4.Петров, А. Вейвлеты и их приложения / А. Петров // Рыбинск – РГАТА – 2007.
Makrush S.V.
SHORT HISTORY, SOME PROPERTIES AND APPLICATIONS OF WAVELET-
ANALYSIS
Belarusian State University, Minsk
Summary
Considered wavelet transform, shows some differences from the Fourier transform, the possible applications.