
- •6. Моделирование процентного риска
- •6.1. Продолжительность и выпуклость портфеля облигаций
- •6.2. Чувствительность текущей стоимости портфеля облигаций к изменению доходности
- •6.3. Чувствительность собственного капитала финансовой организации к изменению доходности облигаций
- •6.4. Иммунизация будущих платежей от процентного риска
Аксень
Э.М. Современные методы финансового
анализа
6. Моделирование процентного риска
6.1. Продолжительность и выпуклость портфеля облигаций
Поскольку портфель облигаций выплачивает последовательность платежей, продолжительность портфеля облигаций находится по формуле (12) главы 2, т.е.
 , (1)
, (1)
где
wk
– доля текущей стоимости k-го
платежа портфеля в текущей стоимости
портфеля,
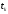 – срок выплатыk-го
платежа портфеля, n
– количество платежей портфеля.
– срок выплатыk-го
платежа портфеля, n
– количество платежей портфеля.
Докажем, что для продолжительности портфеля облигаций справедлива формула:
 ,
(2)
,
(2)
где
wi
–
доля текущей стоимости облигаций i-го
вида в текущей стоимости портфеля,
 – продолжительность облигацииi-го
вида, m
– количество видов облигаций в портфеле.
– продолжительность облигацииi-го
вида, m
– количество видов облигаций в портфеле.
Введем следующие обозначения.
 –количество
облигаций i-го
вида в портфеле,
–количество
облигаций i-го
вида в портфеле,
 – текущая стоимостьk-го
платежа облигации i-го
вида,
– текущая стоимостьk-го
платежа облигации i-го
вида,
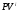 – текущая стоимость облигацииi-го
вида,
– текущая стоимость облигацииi-го
вида,
 – текущая стоимостьk-го
платежа портфеля,
– текущая стоимостьk-го
платежа портфеля,
 – текущая стоимость портфеля,
– текущая стоимость портфеля,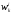 – доля текущей стоимостиk-го
платежа облигации i-го
вида в текущей стоимости облигации i-го
вида.
– доля текущей стоимостиk-го
платежа облигации i-го
вида в текущей стоимости облигации i-го
вида.
Очевидно, что имеют место следующие формулы:
 ,
, 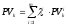 ,
, ,
, (3)
(3)
 ,
,
 ,
,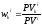 ,
, . (4)
. (4)
С учетом формул (3)-(4), имеем


Таким образом, мы доказали формулу (2).
Пример 1. Портфель облигаций состоит из 40 облигаций первого вида и из 50 облигаций второго вида. Для облигации первого вида: номинальная стоимость – 100 д.е., годовая номинальная купонная ставка – 15%, купонный период – 1 год, до погашения облигации осталось 3 года, годовая эффективная доходность к погашению – 16%. Для облигации второго вида: номинальная стоимость – 120 д.е., годовая номинальная купонная ставка – 20%, купонный период – полугодие, до погашения облигации осталось 5 лет, годовая эффективная доходность к погашению – 18,81%.
Требуется определить продолжительность портфеля облигаций, используя в качестве ставки дисконтирования доходности самих облигаций.
Решение.
Итак,
 д.е.,
д.е.,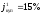 ,
, ,
, ,
, ,
, ,
, д.е.,
д.е.,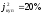 ,
, ,
, лет,
лет, ,
, .
.
Для нахождения продолжительности портфеля облигаций будем использовать формулу (2).
Найдем
продолжительность облигаций первого
и второго вида с помощью формулы (12)
главы 4:
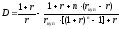 .
.
Поскольку для облигаций первого вида купонный период – год, то для облигаций первого вида купонная ставка и эффективная доходность для купонного периода совпадают с годовой номинальной купонной ставкой и годовой эффективной доходностью. Следовательно,
 лет.
лет.
Для
облигаций второго вида купонная ставка
для купонного периода равна
 ,
эффективная доходность для купонного
периода равна
,
эффективная доходность для купонного
периода равна .
Следовательно,
.
Следовательно,
 .
.
Найдем
доли рыночных стоимостей облигаций
первого и второго вида в рыночной
стоимости портфеля. Для этого вначале
найдем цены облигаций по формуле (6)
главы 4:
 .
.
 ,
,
 .
.

Теперь мы можем найти продолжительность портфеля облигаций по формуле (2):
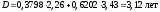
Выпуклость портфеля облигаций определяется по формуле (18) главы 2, т.е.
 . (5)
. (5)
Для выпуклости портфеля облигаций справедлива формула:
 , (6)
, (6)
где
 -
выпуклость облигацииi-го
вида.
-
выпуклость облигацииi-го
вида.
Формула (5) доказывается так же само как формула (2).
6.2. Чувствительность текущей стоимости портфеля облигаций к изменению доходности
Предположим,
что ставка дисконтирования зависит
только от вида облигации. Тогда для
облигаций, входящих в портфель справедлива
формула (13) главы 2:
 .
Таким образом,
.
Таким образом,
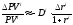 ,
,
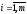 .
(7)
.
(7)
Из (7) следует, что
 ,
,
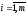 . (8)
. (8)
Легко заметить, что
 . (9)
. (9)
Подставим (8) в (9):
 . (10)
. (10)
Предположим,
что
 не зависит от вида облигации
не зависит от вида облигации .
Тогда из (10) следует, что
.
Тогда из (10) следует, что
 . (11)
. (11)
Разделив
(11) на
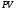 ,
получим:
,
получим:
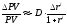 . (12)
. (12)
Итак,
в случае, когда
 не зависит от вида облигации
не зависит от вида облигации ,
для текущей стоимости портфеля облигаций
имеет место формула (12).
,
для текущей стоимости портфеля облигаций
имеет место формула (12).
Замечание.
Если в качестве ставок дисконтирования

 ,
,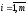 ,
выступают доходности самих облигаций,
то текущие стоимости облигаций
,
выступают доходности самих облигаций,
то текущие стоимости облигаций ,
, ,
равны ценам облигаций, а текущая стоимость
портфеля облигаций
,
равны ценам облигаций, а текущая стоимость
портфеля облигаций равна рыночной стоимости портфеля
облигаций.
равна рыночной стоимости портфеля
облигаций.
Пример
2. Пусть в условиях примера 1
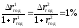 .
Тогда
.
Тогда
 .
.
Несложно
показать, что в случае, когда
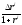 не зависит от вида облигации
не зависит от вида облигации ,
для текущей стоимости портфеля облигаций
имеет место формула:
,
для текущей стоимости портфеля облигаций
имеет место формула:
 . (13)
. (13)
Формула (13) дает более точную оценку для относительного изменения текущей стоимости портфеля облигаций, чем формула (12) (поскольку формула (13) учитывает выпуклость портфеля облигаций). Доказательство формулы (13) аналогично доказательству формулы (12)
