
- •5.8. Описание оценки рыночной стоимости облигации в общем случае
- •5.9. Условия существования имитирующего портфеля и однозначности оценки рыночной стоимости облигации
- •5.10. «Чистые» коэффициенты дисконтирования, их нахождение и использование для оценки рыночной стоимости облигации
- •5.11. Нахождение чистых доходностей методом наименьших квадратов
- •5.12. Форвардные доходности
Аксень Э.М. Современные методы финансового анализа
5.8. Описание оценки рыночной стоимости облигации в общем случае
Пусть
на финансовом рынке m
видов облигаций, выплачивающих платежи
 в моменты времени
в моменты времени .
(Индексi
соответствует виду облигации.) Обозначим
виды этих облигаций
.
(Индексi
соответствует виду облигации.) Обозначим
виды этих облигаций
 .
Цены облигаций
.
Цены облигаций известны и равны
известны и равны .
.
Пусть
некоторая другая облигация
 выплачивает платежи
выплачивает платежи также в моменты времени
также в моменты времени .
Задача заключается в том, чтобы с помощью
цен облигаций
.
Задача заключается в том, чтобы с помощью
цен облигаций оценить рыночную стоимость облигации
оценить рыночную стоимость облигации .
.
Методика
оценки рыночной стоимости облигации
 состоит в построении портфеля из
облигаций
состоит в построении портфеля из
облигаций (цена которых известна), выплачивающих
такие же платежи как и облигация
(цена которых известна), выплачивающих
такие же платежи как и облигация (т.е.
(т.е. ,
, ).
(Такой портфель будем называть имитирующим,
англ.replicating
portfolio.)
На эффективном финансовом рынке цена
имитирующего портфеля должна совпадать
с ценой облигации
).
(Такой портфель будем называть имитирующим,
англ.replicating
portfolio.)
На эффективном финансовом рынке цена
имитирующего портфеля должна совпадать
с ценой облигации
 .
.
Замечание. Мы предполагаем, что все рассматриваемые облигации одинакового качества.
Замечание. Под облигацией мы понимаем любой финансовый инструмент с фиксированными платежами (англ. fixed-income security).
5.9. Условия существования имитирующего портфеля и однозначности оценки рыночной стоимости облигации
Пусть
некоторый портфель
 состоит из облигаций видов
состоит из облигаций видов .
Обозначим через
.
Обозначим через количество облигаций вида
количество облигаций вида в
портфеле. Тогда, во-первых, в моменты
времени
в
портфеле. Тогда, во-первых, в моменты
времени портфель генерирует денежные потоки
портфель генерирует денежные потоки ,
определяемые формулой
,
определяемые формулой
 ,
(23)
,
(23)
и,
во-вторых, цена
 портфеля определяется формулой
портфеля определяется формулой
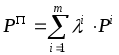 .
(24)
.
(24)
При
оценке рыночной стоимости облигации
 с
помощью (имитирующего) портфеля облигаций
видов
с
помощью (имитирующего) портфеля облигаций
видов могут возникнуть две проблемы. Во-первых,
имитирующий портфель может не существовать,
и во-вторых, имитирующих портфелей может
быть несколько, причем их цена может
быть разной.
могут возникнуть две проблемы. Во-первых,
имитирующий портфель может не существовать,
и во-вторых, имитирующих портфелей может
быть несколько, причем их цена может
быть разной.
Найдем условия, при которых вышеописанные проблемы отсутствуют, т.е. во-первых, имитирующий портфель существует, и во-вторых, если он не единственен, то цены всех имитирующих портфелей равны.
Поскольку удобнее исследовать данные вопросы, используя матрицы и векторы, введем следующие обозначения.
 ,
,
 ,
, ,
, .
(25)
.
(25)
Несложно
заметить, что существование имитирующего
портфеля для любой облигации
 означает,
что для любого вектора платежей
означает,
что для любого вектора платежей должен существовать такой вектор
должен существовать такой вектор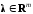 (количеств облигаций
(количеств облигаций в
портфеле), чтобы
в
портфеле), чтобы
 ,
или, что то же самое,
,
или, что то же самое,
 ,
(26)
,
(26)
т.е.
множество значений матрицы
![]() должно
совпадать со всем пространством
должно
совпадать со всем пространством
 ,
что, в свою очередь, равносильно тому,
чтобы ранг матрицы
,
что, в свою очередь, равносильно тому,
чтобы ранг матрицы
 был
равенn.
был
равенn.
Итак,
необходимое и достаточное условие
существования имитирующего портфеля
для любой облигации
 заключается
в равенстве ранга матрицы
заключается
в равенстве ранга матрицы количествуn
платежей облигаций. В дальнейшем будем
ссылаться на это условие как на условие
1.
количествуn
платежей облигаций. В дальнейшем будем
ссылаться на это условие как на условие
1.
Условие
1.
Ранг матрицы
 платежей облигаций
платежей облигаций равен количествуn
платежей этих облигаций.
равен количествуn
платежей этих облигаций.
Теперь
перейдем к вопросу об однозначности
оценки рыночной стоимости облигации
 .
.
Очевидно,
что для однозначности оценки рыночной
стоимости облигации
 необходимо и достаточно, чтобы любые
два разные портфели
необходимо и достаточно, чтобы любые
два разные портфели и
и (с соответствующими векторами
(с соответствующими векторами и
и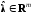 количеств облигаций видов
количеств облигаций видов )
имитирующие облигацию
)
имитирующие облигацию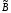 (т.е
(т.е ),
стоили одинаково (т.е., чтобы
),
стоили одинаково (т.е., чтобы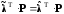 ).
).
Легко
заметить, что это условие равносильно
следующему: для любых
 и
и ,
таких что
,
таких что справедливо
справедливо ,
или, любого вектора
,
или, любого вектора ,
такого что
,
такого что справедливо
справедливо ,
т.е. вектор
,
т.е. вектор должен быть ортогонален ядру матрицы
должен быть ортогонален ядру матрицы![]() .
А
поскольку ядро матрицы
.
А
поскольку ядро матрицы
![]() ортогонально
множеству значений матрицы
ортогонально
множеству значений матрицы
 ,
ортогональность вектора
,
ортогональность вектора
 ядру матрицы
ядру матрицы![]() равносильна
принадлежности вектора
равносильна
принадлежности вектора
 множеству
значений матрицы
множеству
значений матрицы
 .
.
Итак
необходимым и достаточным условием
однозначности оценки рыночной стоимости
облигации
 является
принадлежность вектора
является
принадлежность вектора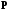 множеству значений матрицы
множеству значений матрицы .
В дальнейшем мы будем ссылаться на это
условие как на условие 2.
.
В дальнейшем мы будем ссылаться на это
условие как на условие 2.
Условие
2.
Вектор
 цен облигаций
цен облигаций ,
принадлежит множеству значений матрицы
,
принадлежит множеству значений матрицы платежей этих облигаций.
платежей этих облигаций.
