
- •1. Общее представление об экономико-математическом моделировании
- •1.1. Определение экономико-математической модели
- •1.2. Классификация экономико-математических моделей
- •1.3. Основные этапы экономико-математического моделирования
- •2. Основы финансовой арифметики
- •2.1. Простой процент
- •Наращенная сумма при простом проценте
- •Текущая стоимость при простом проценте
- •Номинальная годовая процентная ставка
- •3. Математически методы анализа последовательностей платежей
- •3.1. Текущая стоимость последовательности платежей
- •3.2. Будущая стоимость последовательности платежей
- •3.3. Стоимость последовательности платежей в произвольный момент времени
- •4. Моделирование инвестиционных проектов
- •4.1. Дисконтирование денежных потоков инвестиционного проекта
- •4.2. Модель с постоянным процентным ростом свободных денежных потоков
- •4.3. Задача оптимального финансирования проекта
- •4.4. Задача оптимального выбора инвестиционных проектов
- •4.5. Анализ чувствительности денежных потоков проекта
- •4.6. Анализ безубыточности проекта
- •4.7. Влияние инфляции на денежные потоки проекта
- •4.8. Анализ финансового риска инвестиционного проекта
- •4.9. Имитационное моделирование денежных потоков проекта
- •5. Математические методы анализа платежей облигаций
- •5.1. Платежи облигаций
- •5.2. Доходность к погашению облигации
- •5.3. Текущая стоимость облигации
- •5.4. Продолжительность облигации
- •5.5. Чистые доходности
- •5.6. Использование чистых доходностей для оценки рыночной стоимости купонных облигаций
- •5.7. Синтетические бескупонные облигации
- •5.8. Описание оценки рыночной стоимости облигации в общем случае
- •5.9. Условия существования имитирующего портфеля и однозначности оценки рыночной стоимости облигации
- •5.10. «Чистые» коэффициенты дисконтирования, их нахождение и использование для оценки рыночной стоимости облигации
- •5.11. Нахождение чистых доходностей методом наименьших квадратов
- •5.12. Форвардные доходности
- •6. Моделирование процентного риска
- •6.1. Продолжительность и выпуклость портфеля облигаций
- •6.2. Чувствительность текущей стоимости портфеля облигаций к изменению доходности
- •6.3. Чувствительность собственного капитала финансовой организации к изменению доходности облигаций
- •6.4. Иммунизация будущих платежей от процентного риска
- •7. Моделирование кредитного риска
- •7.1. Использование линейной модели вероятности для оценки кредитного риска
- •8. Теория инвестиционного портфеля
- •8.1. Инвестиционный портфель и его основные характеристики
- •8.2. Диверсификация риска
- •8.3. Множество инвестиционных возможностей
- •8.4. Оптимизация инвестиционного портфеля
- •8.5. Множество инвестиционных возможностей при наличии безрисковой доходности
- •8.6. Оптимизация инвестиционного портфеля при наличии безрискового актива
- •8.7. Рыночная модель
- •8.8. Разложение общего риска финансового актива на систематическую и собственную составляющие
- •8.9. Модель оценки финансовых активов
- •9. Математические методы анализа финансовых производных
- •9.1. Основные виды финансовых производных
- •9.2. Рыночная стоимость форвардного контракта
- •9.3. Соотношение между рыночной стоимостью форвардного контракта и форвардной ценой базового актива
- •9.4. Форвардные контракты на покупку валюты
- •9.5. Форвардные контракты на процентные ставки
- •9.6. Фьючерсные контракты
- •9.7. Микрохеджирование с помощью фьючерсных контрактов
- •9.8. Макрохеджирование с помощью фьючерсных контрактов
8.9. Модель оценки финансовых активов
В
модели оценки финансовых активов
(сокращенно CAPM
от capital
asset
pricing model)
предполагается, что все инвесторы имеют
полную информацию о всех финансовых
активах (т.е. знают ожидаемые доходности
![]() ,
,![]() ,
стандартные отклонения
,
стандартные отклонения![]() и ковариации
и ковариации![]() )
и действуют рационально (т.е. стремятся
увеличить доходность портфеля и уменьшить
его риск).
)
и действуют рационально (т.е. стремятся
увеличить доходность портфеля и уменьшить
его риск).
Тогда
при наличии безрискового актива каждый
инвестор будет строить портфель
![]() ,
обеспечивающий эффективную границу
множества инвестиционных возможностей
комбинаций безрискового актива и
портфелей рисковых активов (см. параграф
7.6).
,
обеспечивающий эффективную границу
множества инвестиционных возможностей
комбинаций безрискового актива и
портфелей рисковых активов (см. параграф
7.6).
![]()
![]()


![]()
![]()
![]()
![]()

![]()
Такой портфель является решением задачи (60)-(62):
![]() , (60)
, (60)
![]() , (61)
, (61)
![]() , (62)
, (62)
где
![]() – тангенс угла наклона луча
– тангенс угла наклона луча![]() .
.
Для
простоты ограничимся рассмотрением
случая, когда оптимальный портфель
![]() задачи (60)-(62) единственен. Тогда (в
условиях моделиCAPM)
все инвесторы будут строить один и тот
же портфель
задачи (60)-(62) единственен. Тогда (в
условиях моделиCAPM)
все инвесторы будут строить один и тот
же портфель
![]() .
(Вообще говоря, количества
.
(Вообще говоря, количества![]() финансовых активов в портфелях разных
инвесторов могут отличаться, однако
доли
финансовых активов в портфелях разных
инвесторов могут отличаться, однако
доли![]() должны совпадать.) Следовательно, доли
финансовых активов в суммарном портфеле
всех инвесторов равны соответствующим
долям
должны совпадать.) Следовательно, доли
финансовых активов в суммарном портфеле
всех инвесторов равны соответствующим
долям![]() в оптимальном портфеле
в оптимальном портфеле![]() .
.
С другой стороны, поскольку суммарный портфель всех инвесторов состоит из всех финансовых активов в экономике, суммарный портфель совпадает с рыночным портфелем.
Следовательно,
доли финансовых активов
![]() в оптимальном портфеле
в оптимальном портфеле![]() равны соответствующим долям
равны соответствующим долям![]() в рыночном портфеле.
в рыночном портфеле.
Замечание
16. В рыночном портфеле доли
![]() всех финансовых активов положительны
(и меньше единицы).
всех финансовых активов положительны
(и меньше единицы).
Замечание
17. Поскольку рыночный портфель
![]() является (единственным) оптимальным
портфелем задачи (60)-(62), коэффициент
является (единственным) оптимальным
портфелем задачи (60)-(62), коэффициент![]() (соответствующий рыночному портфелю)
больше коэффициента
(соответствующий рыночному портфелю)
больше коэффициента![]() любого другого портфеля
любого другого портфеля![]() ,
т.е
,
т.е
![]()
![]() . (84)
. (84)
Основной результат модели CAPM состоит в том, что для любого финансового актива справедливо равенство:
![]() , (85)
, (85)
где
коэффициент
![]() определен формулой:
определен формулой:
![]() . (86)
. (86)
Замечание
18. Отметим, что в условиях рыночной
коэффициент
![]() также может вычисляться по формуле (98)
(см. формулу (68)). Однако в условиях моделиCAPM
предположения рыночной модели могут
не выполняться.
также может вычисляться по формуле (98)
(см. формулу (68)). Однако в условиях моделиCAPM
предположения рыночной модели могут
не выполняться.
Замечание
19. Из формулы (86) следует, что для
безрискового актива
![]() ,
а для рыночного портфеля
,
а для рыночного портфеля![]() .
.
Равенство
(85) представляет собой уравнение прямой
в координатной плоскости
![]() ,
проходящую через точки
,
проходящую через точки![]() и
и![]() .
Эту прямую называют рыночной линией
финансового актива (security
market
line).
.
Эту прямую называют рыночной линией
финансового актива (security
market
line).
![]()


![]()
![]()


![]()
![]()

1
![]()
Докажем
равенство (85). Для этого построим портфель
![]() следующим образом: портфель
следующим образом: портфель![]() представляет
собой комбинацию финансового активаi–го
вида и рыночного портфеля
представляет
собой комбинацию финансового активаi–го
вида и рыночного портфеля
![]() ,
причем в такой комбинации доля активаi–го
вида равна
,
причем в такой комбинации доля активаi–го
вида равна
![]() ,
а доля рыночного портфеля равна
,
а доля рыночного портфеля равна![]() .
.
Обозначим
через
![]() и
и![]() ожидаемую доходность и стандартное
отклонение доходности портфеля
ожидаемую доходность и стандартное
отклонение доходности портфеля![]() .
В соответствием с определением портфеля
.
В соответствием с определением портфеля![]() из формул (19) и (28) следует, что
из формул (19) и (28) следует, что
![]() , (87)
, (87)
![]() . (88)
. (88)
Очевидно,
что доли
![]() и
и![]() (
(![]() )
финансовых активов в портфеле
)
финансовых активов в портфеле![]() определяются следующим образом:
определяются следующим образом:
![]() , (89)
, (89)
![]()
![]() . (90)
. (90)
Замечание
20. Мы предполагаем, что доли (рисковых)
финансовых активов в рассматриваемых
нами портфелях неотрицательны. Для
неотрицательности долей
![]() и
и![]() (рассчитываемых по формулам (89) и (90))
необходимо и достаточно, чтобы
(рассчитываемых по формулам (89) и (90))
необходимо и достаточно, чтобы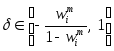 .
Поскольку (в соответствии с Замечанием
16)
.
Поскольку (в соответствии с Замечанием
16)![]() , значение выражения
, значение выражения![]() определено и отрицательно. Следовательно,
при достаточно малых по модулю (как
положительных, так и отрицательных)
значениях
определено и отрицательно. Следовательно,
при достаточно малых по модулю (как
положительных, так и отрицательных)
значениях![]() портфель
портфель![]() состоит
из неотрицательных долей финансовых
активов. То, что параметр
состоит
из неотрицательных долей финансовых
активов. То, что параметр![]() может
принимать как положительные, так и
отрицательные значения будет использовано
ниже при доказательстве равенства (85).
может
принимать как положительные, так и
отрицательные значения будет использовано
ниже при доказательстве равенства (85).
Обозначим
![]() коэффицент
коэффицент![]() портфеля
портфеля![]() ,
т.е
,
т.е
![]() . (91)
. (91)
Замечание
21. Поскольку рыночный портфель
![]() является оптимальным портфелем задачи
(60)-(62), то при любых допустимых значениях
является оптимальным портфелем задачи
(60)-(62), то при любых допустимых значениях![]() (т.е.при
(т.е.при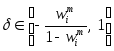 ),
в соответствии с Замечанием 17,
),
в соответствии с Замечанием 17,
![]() . (92)
. (92)
Заметим,
что при
![]() портфель
портфель![]() совпадает с рыночным портфелем
совпадает с рыночным портфелем![]() ,
и следовательно, при
,
и следовательно, при![]()
![]() .
Отсюда следует, что
.
Отсюда следует, что
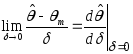 . (93)
. (93)
Докажем, что
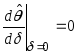 . (94)
. (94)
Доказательство равенства (94) проведем от противного.
Предположим,
что
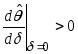 .
Тогда, как следует из равенства (93), при
достаточно малых по модулю
.
Тогда, как следует из равенства (93), при
достаточно малых по модулю![]() выражение
выражение![]() положительно, и, следовательно, при
достаточно малых положительных
положительно, и, следовательно, при
достаточно малых положительных![]()
![]() ,
что противоречит оптимальности рыночного
портфеля (см. Замечание 21).
,
что противоречит оптимальности рыночного
портфеля (см. Замечание 21).
Замечание
22. Если бы
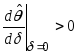 ,
то рыночный портфель можно было бы
улучшить, увеличив в нем долю активаi-го
вида.
,
то рыночный портфель можно было бы
улучшить, увеличив в нем долю активаi-го
вида.
Предположим,
что
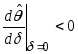 .
Тогда, как следует из равенства (93), при
достаточно малых по модулю
.
Тогда, как следует из равенства (93), при
достаточно малых по модулю![]() выражение
выражение![]() отрицательно, и, следовательно, при
достаточно малых отрицательных
отрицательно, и, следовательно, при
достаточно малых отрицательных![]()
![]() ,
что противоречит оптимальности рыночного
портфеля (см. Замечание 21).
,
что противоречит оптимальности рыночного
портфеля (см. Замечание 21).
Замечание
23. Если бы
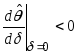 ,
то рыночный портфель можно было бы
улучшить, уменьшив в нем долю активаi-го
вида.
,
то рыночный портфель можно было бы
улучшить, уменьшив в нем долю активаi-го
вида.
Поскольку,
как мы доказали, производная
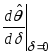 не
может быть ни положительной, ни
отрицательной, то она равна нулю.
не
может быть ни положительной, ни
отрицательной, то она равна нулю.
Найдем
производную
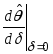 .
С помощью формулы (91) имеем:
.
С помощью формулы (91) имеем:
![]() . (95)
. (95)
При
![]() формула (95) примет вид:
формула (95) примет вид:
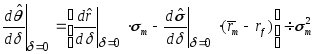 . (96)
. (96)
Из формул (87) и (88) следует, что
![]() , (97)
, (97)
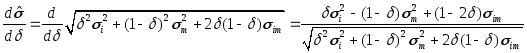 . (98)
. (98)
При
![]() формула (98) примет вид:
формула (98) примет вид:
![]() . (99)
. (99)
Подставив (97), (99) в (96), получим
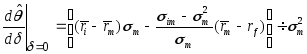 . (100)
. (100)
Из формулы (86) следует, что
![]() . (101)
. (101)
Подставив эту формулу в равенство (100), получим
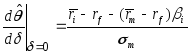 . (102)
. (102)
Из
равенства производной
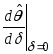 нулю (см. соотношение (94)) и из формулы
(102) очевидным образом следует равенство
(85) (основной результат моделиCAPM):
нулю (см. соотношение (94)) и из формулы
(102) очевидным образом следует равенство
(85) (основной результат моделиCAPM):
![]() , (85)
, (85)
Замечание
24. Если бы
![]() ,
то (в силу формулы (102)) производная
,
то (в силу формулы (102)) производная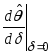 была
бы положительной, и, следовательно (см.
замечание 22), рыночный портфель можно
было бы улучшить, увеличив долю активаi-го
вида в портфеле.
была
бы положительной, и, следовательно (см.
замечание 22), рыночный портфель можно
было бы улучшить, увеличив долю активаi-го
вида в портфеле.
Если
бы
![]() ,
то (в силу формулы (102)) производная
,
то (в силу формулы (102)) производная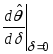 была
бы отрицательной, и, следовательно (см.
замечание 23), рыночный портфель можно
было бы улучшить, уменьшив долю активаi-го
вида в портфеле.
была
бы отрицательной, и, следовательно (см.
замечание 23), рыночный портфель можно
было бы улучшить, уменьшив долю активаi-го
вида в портфеле.
