
- •1. Общее представление об экономико-математическом моделировании
- •1.1. Определение экономико-математической модели
- •1.2. Классификация экономико-математических моделей
- •1.3. Основные этапы экономико-математического моделирования
- •2. Основы финансовой арифметики
- •2.1. Простой процент
- •Наращенная сумма при простом проценте
- •Текущая стоимость при простом проценте
- •Номинальная годовая процентная ставка
- •3. Математически методы анализа последовательностей платежей
- •3.1. Текущая стоимость последовательности платежей
- •3.2. Будущая стоимость последовательности платежей
- •3.3. Стоимость последовательности платежей в произвольный момент времени
- •4. Моделирование инвестиционных проектов
- •4.1. Дисконтирование денежных потоков инвестиционного проекта
- •4.2. Модель с постоянным процентным ростом свободных денежных потоков
- •4.3. Задача оптимального финансирования проекта
- •4.4. Задача оптимального выбора инвестиционных проектов
- •4.5. Анализ чувствительности денежных потоков проекта
- •4.6. Анализ безубыточности проекта
- •4.7. Влияние инфляции на денежные потоки проекта
- •4.8. Анализ финансового риска инвестиционного проекта
- •4.9. Имитационное моделирование денежных потоков проекта
- •5. Математические методы анализа платежей облигаций
- •5.1. Платежи облигаций
- •5.2. Доходность к погашению облигации
- •5.3. Текущая стоимость облигации
- •5.4. Продолжительность облигации
- •5.5. Чистые доходности
- •5.6. Использование чистых доходностей для оценки рыночной стоимости купонных облигаций
- •5.7. Синтетические бескупонные облигации
- •5.8. Описание оценки рыночной стоимости облигации в общем случае
- •5.9. Условия существования имитирующего портфеля и однозначности оценки рыночной стоимости облигации
- •5.10. «Чистые» коэффициенты дисконтирования, их нахождение и использование для оценки рыночной стоимости облигации
- •5.11. Нахождение чистых доходностей методом наименьших квадратов
- •5.12. Форвардные доходности
- •6. Моделирование процентного риска
- •6.1. Продолжительность и выпуклость портфеля облигаций
- •6.2. Чувствительность текущей стоимости портфеля облигаций к изменению доходности
- •6.3. Чувствительность собственного капитала финансовой организации к изменению доходности облигаций
- •6.4. Иммунизация будущих платежей от процентного риска
- •7. Моделирование кредитного риска
- •7.1. Использование линейной модели вероятности для оценки кредитного риска
- •8. Теория инвестиционного портфеля
- •8.1. Инвестиционный портфель и его основные характеристики
- •8.2. Диверсификация риска
- •8.3. Множество инвестиционных возможностей
- •8.4. Оптимизация инвестиционного портфеля
- •8.5. Множество инвестиционных возможностей при наличии безрисковой доходности
- •8.6. Оптимизация инвестиционного портфеля при наличии безрискового актива
- •8.7. Рыночная модель
- •8.8. Разложение общего риска финансового актива на систематическую и собственную составляющие
- •8.9. Модель оценки финансовых активов
- •9. Математические методы анализа финансовых производных
- •9.1. Основные виды финансовых производных
- •9.2. Рыночная стоимость форвардного контракта
- •9.3. Соотношение между рыночной стоимостью форвардного контракта и форвардной ценой базового актива
- •9.4. Форвардные контракты на покупку валюты
- •9.5. Форвардные контракты на процентные ставки
- •9.6. Фьючерсные контракты
- •9.7. Микрохеджирование с помощью фьючерсных контрактов
- •9.8. Макрохеджирование с помощью фьючерсных контрактов
8.2. Диверсификация риска
Диверсификация риска – это уменьшение риска за счет вложения денежных средств в финансовые активы разных видов.
Из формулы (19) следует, что ожидаемая доходность инвестиционного портфеля равна средневзвешенной ожидаемой доходности входящих в него финансовых активов.
Покажем, что стандартное отклонение доходности инвестиционного портфеля не превосходит средневзвешенного стандартного отклонения доходностей входящих в него финансовых активов.
Из теории вероятностей известно, что коэффициент корреляции двух случайных величин по модулю не превосходит единицы. Следовательно,
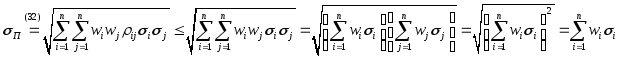 .
.
Итак,
![]() . (33)
. (33)
Причем,
![]() в том и только в том случае, когда
в том и только в том случае, когда![]()
![]() ,
и
,
и![]() ,
если хотя бы для двух финансовых активов
,
если хотя бы для двух финансовых активов![]() .
.
Поскольку в абсолютном большинстве случаев коэффициент корреляции доходностей двух (разных) финансовых активов меньше единицы, стандартное отклонение доходности портфеля как правило меньше средневзвешенного стандартного отклонения доходностей входящих в него финансовых активов.
Для
того, чтобы лучше понять , что такое
диверсификация риска, рассмотрим частный
случай, когда инвестиционный портфель
состоит из финансовых активов с
одинаковыми характеристиками, т.е. когда
![]() и
и![]()
![]() .
.
В
этом случае,
![]() ,
,![]() .
.
Таким
образом,
![]() и
и![]() ,
причем
,
причем![]() ,
если хотя бы для двух финансовых активов
,
если хотя бы для двух финансовых активов![]() .
Следовательно, в случае, когда
инвестиционный портфель состоит из
финансовых активов с одинаковыми
характеристиками, ожидаемая доходность
портфеля равна ожидаемой доходности
входящих в него активов, а стандартное
отклонение доходности инвестиционного
портфеля не превосходит стандартного
отклонения доходностей входящих в него
активов, причем стандартное отклонение
доходности инвестиционного портфеля
меньше стандартного отклонения
доходностей входящих в него активов,
если хотя бы для двух финансовых активов
.
Следовательно, в случае, когда
инвестиционный портфель состоит из
финансовых активов с одинаковыми
характеристиками, ожидаемая доходность
портфеля равна ожидаемой доходности
входящих в него активов, а стандартное
отклонение доходности инвестиционного
портфеля не превосходит стандартного
отклонения доходностей входящих в него
активов, причем стандартное отклонение
доходности инвестиционного портфеля
меньше стандартного отклонения
доходностей входящих в него активов,
если хотя бы для двух финансовых активов![]() .
.
8.3. Множество инвестиционных возможностей
Множество
инвестиционных возможностей
![]() – это множество векторов
– это множество векторов![]() ,
таких, что существует инвестиционный
портфель, стандартное отклонение
доходности которого равно
,
таких, что существует инвестиционный
портфель, стандартное отклонение
доходности которого равно![]() ,
и ожидаемая доходность которого равна
,
и ожидаемая доходность которого равна![]() .
Поскольку стандартное отклонение
доходности портфеля и ожидаемая
доходность портфеля определяются с
помощью долей
.
Поскольку стандартное отклонение
доходности портфеля и ожидаемая
доходность портфеля определяются с
помощью долей![]() ,
,![]() ,
по формулам (19) и (25),
,
по формулам (19) и (25),
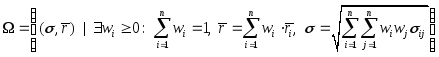 . (34)
. (34)
Рассмотрим
частный случай, когда портфели состоят
из двух видов финансовых активов видов![]() и
и![]() .
Для определенности будем считать, что
.
Для определенности будем считать, что![]() и
и![]() .
Из формул (19) и (28) следует, что,
.
Из формул (19) и (28) следует, что,
![]() , (35)
, (35)
![]() . (36)
. (36)
Кроме того, как следует из равенства (18),
![]() . (37)
. (37)
Из (37) следует, что
![]() . (38)
. (38)
Поскольку
доли
![]() и
и![]() неотрицательны, и из (35) и (37) следует,
что ожидаемая доходность портфеля
неотрицательны, и из (35) и (37) следует,
что ожидаемая доходность портфеля![]() может принимать любое значение на
отрезке
может принимать любое значение на
отрезке![]() .
Из (35) и (37) также следует, что
.
Из (35) и (37) также следует, что
![]() , (39)
, (39)
![]() . (40)
. (40)
Подставив формулы (39), (40) в (36) получим:
![]() . (41)
. (41)
Из
(41) в частности следует, в данном случае
стандартное отклонение отклонение
доходности портфеля
![]() однозначно определяется ожидаемой
доходностью портфеля
однозначно определяется ожидаемой
доходностью портфеля![]() и непрерывно зависит от нее. Следовательно,
график множества инвестиционных
возможностей в координатной плоскости
и непрерывно зависит от нее. Следовательно,
график множества инвестиционных
возможностей в координатной плоскости![]() в данном случае представляет собой
кривую с концами в точках
в данном случае представляет собой
кривую с концами в точках![]() и
и![]() .
.
Неравенство (33) в данном случае имеет вид:
![]() . (42)
. (42)
При
этом
![]() в том и только в том случае, когда
в том и только в том случае, когда![]() .
(Если же
.
(Если же![]() ,
то
,
то![]() .)
.)
Подставив формулы (39) и (40) в правую часть неравенства (42), получим
![]() . (43)
. (43)
Заметим,
что в координатной плоскости
![]() график функции
график функции![]() представляет собой прямую, проходящую
через точки
представляет собой прямую, проходящую
через точки![]() и
и![]() .
.
Следовательно,
из соотношений (42) и (43) вытекает, что при
![]() точка
точка![]() расположена левее точки
расположена левее точки![]() ,
лежащей на отрезке
,
лежащей на отрезке![]() ,
в случае, когда
,
в случае, когда![]() ,
а в случае, когда
,
а в случае, когда![]() ,
точка
,
точка![]() лежит
на отрезке
лежит
на отрезке![]() .
.
Таким
образом, график множества инвестиционных
возможностей представляет собой кривую,
расположенную слева от отрезка ![]() ,
в случае, когда
,
в случае, когда![]() ,
и отрезок
,
и отрезок![]() в
случае, когда
в
случае, когда![]() .
.



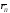

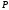



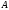

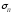

В случае, когда количество видов финансовых активов в инвестиционных портфелях больше двух, стандартное отклонение доходности портфеля не определяется однозначно ожидаемой доходностью портфеля. Следовательно, в этом случае график множества инвестиционных возможностей представляет собой двухмерную фигуру.

![]()
![]()


![]()
Напомним, что в теории инвестиционного портфеля основные характеристики портфеля – это ожидаемая доходность и стандартное отклонение доходности. Рационально действующий инвестор будет стараться построить портфель с большей ожидаемой доходностью и меньшим риском.





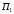

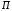


В
данном примере (см. рис.) рационально
действующий инвестор портфелю
![]() предпочтет любой из портфелей
предпочтет любой из портфелей![]() ,
,![]() ,
,![]() .
Однако какой именно портфель из портфелей
.
Однако какой именно портфель из портфелей![]() ,
,![]() ,
,![]() предпочтет инвестор сказать трудно.
предпочтет инвестор сказать трудно.
Итак, рационально действующий инвестор попытается построить такой портфель, для которого нельзя улучшить ни одну из его характеристик, не ухудшив при этом другую. Такие портфели называются эффективными.
Дадим строгое определение эффективного портфеля.
Портфель
![]() с ожидаемой доходностью
с ожидаемой доходностью![]() и стандартным отклонением доходности
и стандартным отклонением доходности![]() называется эффективным, если не существует
портфель
называется эффективным, если не существует
портфель![]() с ожидаемой доходностью
с ожидаемой доходностью![]() и стандартным отклонением доходности
и стандартным отклонением доходности![]() ,
такой, что либо
,
такой, что либо![]() и при этом
и при этом![]() ,
либо
,
либо![]() и при этом
и при этом![]() .
.
Замечание 10. Понятие эффективности инвестиционного портфеля является частным случаем понятия эффективности по Парето.
Отметим,
что эффективный портфель не единственен.
В примере, изображенном на рисунке,
любой из портфелей
![]() ,
,![]() ,
,![]() является эффективным.
является эффективным.
Множество
векторов
![]() характеристик
всех эффективных портфелей называется
эффективной границей множества
инвестиционных возможностей. Обозначим
эффективную границу через
характеристик
всех эффективных портфелей называется
эффективной границей множества
инвестиционных возможностей. Обозначим
эффективную границу через![]() .
.
Эффективная
граница
![]() представляет собой часть границы
множества инвестиционных возможностей,
расположенную между самой верхней и
самой левой точкой множества инвестиционных
возможностей.
представляет собой часть границы
множества инвестиционных возможностей,
расположенную между самой верхней и
самой левой точкой множества инвестиционных
возможностей.
