
- •1. Общее представление об экономико-математическом моделировании
- •1.1. Определение экономико-математической модели
- •1.2. Классификация экономико-математических моделей
- •1.3. Основные этапы экономико-математического моделирования
- •2. Основы финансовой арифметики
- •2.1. Простой процент
- •Наращенная сумма при простом проценте
- •Текущая стоимость при простом проценте
- •Номинальная годовая процентная ставка
- •3. Математически методы анализа последовательностей платежей
- •3.1. Текущая стоимость последовательности платежей
- •3.2. Будущая стоимость последовательности платежей
- •3.3. Стоимость последовательности платежей в произвольный момент времени
- •4. Моделирование инвестиционных проектов
- •4.1. Дисконтирование денежных потоков инвестиционного проекта
- •4.2. Модель с постоянным процентным ростом свободных денежных потоков
- •4.3. Задача оптимального финансирования проекта
- •4.4. Задача оптимального выбора инвестиционных проектов
- •4.5. Анализ чувствительности денежных потоков проекта
- •4.6. Анализ безубыточности проекта
- •4.7. Влияние инфляции на денежные потоки проекта
- •4.8. Анализ финансового риска инвестиционного проекта
- •4.9. Имитационное моделирование денежных потоков проекта
- •5. Математические методы анализа платежей облигаций
- •5.1. Платежи облигаций
- •5.2. Доходность к погашению облигации
- •5.3. Текущая стоимость облигации
- •5.4. Продолжительность облигации
- •5.5. Чистые доходности
- •5.6. Использование чистых доходностей для оценки рыночной стоимости купонных облигаций
- •5.7. Синтетические бескупонные облигации
- •5.8. Описание оценки рыночной стоимости облигации в общем случае
- •5.9. Условия существования имитирующего портфеля и однозначности оценки рыночной стоимости облигации
- •5.10. «Чистые» коэффициенты дисконтирования, их нахождение и использование для оценки рыночной стоимости облигации
- •5.11. Нахождение чистых доходностей методом наименьших квадратов
- •5.12. Форвардные доходности
- •6. Моделирование процентного риска
- •6.1. Продолжительность и выпуклость портфеля облигаций
- •6.2. Чувствительность текущей стоимости портфеля облигаций к изменению доходности
- •6.3. Чувствительность собственного капитала финансовой организации к изменению доходности облигаций
- •6.4. Иммунизация будущих платежей от процентного риска
- •7. Моделирование кредитного риска
- •7.1. Использование линейной модели вероятности для оценки кредитного риска
- •8. Теория инвестиционного портфеля
- •8.1. Инвестиционный портфель и его основные характеристики
- •8.2. Диверсификация риска
- •8.3. Множество инвестиционных возможностей
- •8.4. Оптимизация инвестиционного портфеля
- •8.5. Множество инвестиционных возможностей при наличии безрисковой доходности
- •8.6. Оптимизация инвестиционного портфеля при наличии безрискового актива
- •8.7. Рыночная модель
- •8.8. Разложение общего риска финансового актива на систематическую и собственную составляющие
- •8.9. Модель оценки финансовых активов
- •9. Математические методы анализа финансовых производных
- •9.1. Основные виды финансовых производных
- •9.2. Рыночная стоимость форвардного контракта
- •9.3. Соотношение между рыночной стоимостью форвардного контракта и форвардной ценой базового актива
- •9.4. Форвардные контракты на покупку валюты
- •9.5. Форвардные контракты на процентные ставки
- •9.6. Фьючерсные контракты
- •9.7. Микрохеджирование с помощью фьючерсных контрактов
- •9.8. Макрохеджирование с помощью фьючерсных контрактов
5.11. Нахождение чистых доходностей методом наименьших квадратов
На
практике обычно количество видов
облигаций m
намного превышает количество n
моментов времени, в которые выплачиваются
платежи облигаций. В таких случаях чаще
всего система уравнений (42) не имеет
точного решения
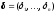 .
Однако можно найти приближенное решение
этой системы.
.
Однако можно найти приближенное решение
этой системы.
Приближенной
решение системы (42) состоит в подборе
таких значений
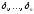 ,
чтобы сумма квадратов отклонений левых
частей уравнений системы (42) от правых
частей уравнений этой системы была
минимальна, т.е. минимизируется
,
чтобы сумма квадратов отклонений левых
частей уравнений системы (42) от правых
частей уравнений этой системы была
минимальна, т.е. минимизируется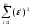 ,
где
,
где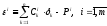 .
.
Замечание.
Поскольку (исходя из экономического
смысла) коэффициенты дисконтирования
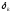 не должны увеличиваться с увеличением
сроков платежей
не должны увеличиваться с увеличением
сроков платежей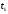 ,
,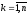 ,
обычно
,
обычно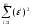 минимизируется при ограничении:
минимизируется при ограничении: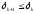 ,
,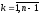 .
.
С
помощью полученных таким образом
коэффициентов дисконтирования
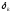 чистые доходности
чистые доходности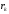 находятся по формуле (31).
находятся по формуле (31).
5.12. Форвардные доходности
Вначале
рассмотрим понятие форвардных доходностей
на примере. Предположим, что инвестор
хочет вложить деньги в облигации на два
года. Пусть на финансовом рынке имеются
однолетние и двухлетние бескупонные
облигации с доходностями
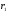 и
и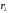 ,
соответственно. Тогда инвестор может
вложить деньги в облигации на два года
следующими двумя способами:
,
соответственно. Тогда инвестор может
вложить деньги в облигации на два года
следующими двумя способами:
Вложить деньги в двухлетние бескупонные облигации.
Вложить деньги в однолетние бескупонные облигации (на один год). Затем, в начале второго года, реинвестировать доход в бескупонные облигации со сроком погашения в конце второго года.
Обозначим
начальный капитал инвестора через P.
Тогда при первой инвестиционной стратегии
доход инвестора в конце второго года
составит
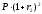 д.е.
д.е.
При
второй инвестиционной стратегии доход
инвестора в конце первого года составит
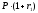 д.е. Поскольку в начале второго года всю
эту сумму (в соответствии со второй
инвестиционной стратегией) инвестор
вкладывает в бескупонные облигации со
сроком погашения в конце второго года,
доход инвестора составит
д.е. Поскольку в начале второго года всю
эту сумму (в соответствии со второй
инвестиционной стратегией) инвестор
вкладывает в бескупонные облигации со
сроком погашения в конце второго года,
доход инвестора составит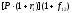 д.е., где
д.е., где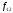 – доходность бескупонных облигаций со
сроком погашения в конце второго года,
найденная с помощью рыночной цены таких
облигаций в начале второго года. (Заметим,
что доходность
– доходность бескупонных облигаций со
сроком погашения в конце второго года,
найденная с помощью рыночной цены таких
облигаций в начале второго года. (Заметим,
что доходность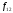 не известна в начале первого года.) Итак,
при второй инвестиционной стратегии
доход инвестора в конце второго года
составит
не известна в начале первого года.) Итак,
при второй инвестиционной стратегии
доход инвестора в конце второго года
составит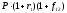 д.е.
д.е.
Под
форвардной доходностью
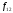 понимают такое значение доходности
понимают такое значение доходности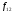 ,
при котором первая и вторая инвестиционная
стратегии обеспечивают одинаковый
доход в конце второго года, т.е. при
котором
,
при котором первая и вторая инвестиционная
стратегии обеспечивают одинаковый
доход в конце второго года, т.е. при
котором
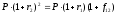 .
(44)
.
(44)
Итак,
форвардная доходность
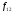 определяется из уравнения (44). Решив это
уравнение, получим:
определяется из уравнения (44). Решив это
уравнение, получим:
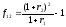 . (45)
. (45)
Пример
12. В условиях примера 8 требуется найти
форвардную доходность
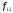 .
.
Решение.
В результате решения примера 8 мы
получили:
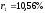 ,
,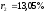 .
.
Подставив
эти значения в формулу (45), получим:
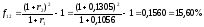 .
.
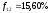 означает,
что если вложить деньги в однолетние
бескупонные облигации с доходностью
означает,
что если вложить деньги в однолетние
бескупонные облигации с доходностью
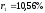 ,
а затем, в начале второго года,
реинвестировать доход в бескупонные
облигации со сроком погашения в конце
второго года и с доходностью
,
а затем, в начале второго года,
реинвестировать доход в бескупонные
облигации со сроком погашения в конце
второго года и с доходностью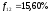 ,
то полученный в конце второго года доход
будет равен доходу, полученному при
вложении денег в двухлетние бескупонные
облигации с доходностью
,
то полученный в конце второго года доход
будет равен доходу, полученному при
вложении денег в двухлетние бескупонные
облигации с доходностью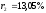 .
.
В случае, если на финансовом рынке отсутствуют бескупонные облигации, то при определении форвардной доходности используются доходности синтетических бескупонных облигаций (чистые доходности).
Пример
13.
В условиях примера 11 требуется найти
форвардную доходность
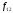 .
.
Решение.
В результате решения примера 11 мы
получили значения для чистых доходностей:
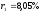 ,
,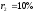 .
Найдем форвардную доходность
.
Найдем форвардную доходность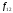 по формуле (45):
по формуле (45):
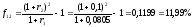 .
.
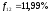 означает,
что если вложить деньги в однолетние
синтетические бескупонные облигации
с доходностью
означает,
что если вложить деньги в однолетние
синтетические бескупонные облигации
с доходностью
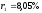 ,
а затем, в начале второго года,
реинвестировать доход в синтетические
бескупонные облигации со сроком погашения
в конце второго года и с доходностью
,
а затем, в начале второго года,
реинвестировать доход в синтетические
бескупонные облигации со сроком погашения
в конце второго года и с доходностью ,
то полученный в конце второго года доход
будет равен доходу, полученному при
вложении денег в двухлетние синтетические
бескупонные облигации с доходностью
,
то полученный в конце второго года доход
будет равен доходу, полученному при
вложении денег в двухлетние синтетические
бескупонные облигации с доходностью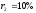 .
.
Данное
выше определение форвардной доходности
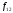 естественным образом обобщается на
случай
естественным образом обобщается на
случай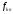 .
А именно, форвардная доходность
.
А именно, форвардная доходность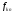 – это такое значение доходности
бескупонных облигаций со сроком погашения
в конце периода времениn,
найденная с помощью рыночной цены таких
облигаций в начале периода
– это такое значение доходности
бескупонных облигаций со сроком погашения
в конце периода времениn,
найденная с помощью рыночной цены таких
облигаций в начале периода
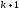 ,
которое обеспечивает одинаковые доходы
для следующих двух инвестиционных
стратегий:
,
которое обеспечивает одинаковые доходы
для следующих двух инвестиционных
стратегий:
Вложить деньги в бескупонные облигации со сроком погашения в конце периода n.
Вложить деньги в бескупонные облигации со сроком погашения в конце периода k. Затем, в начале периода
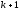 реинвестировать доход в бескупонные
облигации со сроком погашения в конце
периодаn.
реинвестировать доход в бескупонные
облигации со сроком погашения в конце
периодаn.
В
соответствии с данным определением,
форвардная доходность
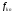 находится из уравнения:
находится из уравнения:
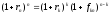 , (46)
, (46)
где
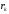 – доходность бескупонных облигаций со
сроком погашения в конце периодаk,
а
– доходность бескупонных облигаций со
сроком погашения в конце периодаk,
а
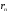 – доходность бескупонных облигаций со
сроком погашения в конце периодаn.
– доходность бескупонных облигаций со
сроком погашения в конце периодаn.
В случае, если на финансовом рынке отсутствуют бескупонные облигации, то при определении форвардной доходности используются доходности синтетических бескупонных облигаций (чистые доходности).
Решив уравнение (46), получим:
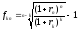 . (47)
. (47)
Иногда
при определении форвардных доходностей
удобно использовать аппарат, разработанный
в случае непрерывной капитализации
процента. Дадим определение (непрерывно
капитализируемой) форвардной доходности
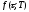 .
Форвардная доходность
.
Форвардная доходность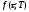 – это такое значение (непрерывно
капитализируемой) доходности бескупонных
облигаций со сроком погашения в момент
времениT,
найденная с помощью рыночной цены таких
облигаций в момент времени
– это такое значение (непрерывно
капитализируемой) доходности бескупонных
облигаций со сроком погашения в момент
времениT,
найденная с помощью рыночной цены таких
облигаций в момент времени
 ,
которое обеспечивает одинаковые доходы
для следующих двух инвестиционных
стратегий:
,
которое обеспечивает одинаковые доходы
для следующих двух инвестиционных
стратегий:
Вложить деньги в бескупонные облигации со сроком погашения в момент времени T.
Вложить деньги в бескупонные облигации со сроком погашения в момент времени
 и реинвестировать доход (полученный в
момент времени
и реинвестировать доход (полученный в
момент времени )
в бескупонные облигации со сроком
погашения в момент времениT.
)
в бескупонные облигации со сроком
погашения в момент времениT.
В
соответствии с данным определением,
форвардная доходность
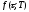 находится из уравнения:
находится из уравнения:
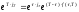 ,
(48)
,
(48)
где
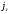 – непрерывно капитализируемая доходность
бескупонных облигаций со сроком погашения
в момент времени
– непрерывно капитализируемая доходность
бескупонных облигаций со сроком погашения
в момент времени ,
а
,
а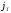 – непрерывно капитализируемая доходность
бескупонных облигаций со сроком погашения
в момент времениT.
– непрерывно капитализируемая доходность
бескупонных облигаций со сроком погашения
в момент времениT.
Очевидным образом уравнение (48) сводится к следующему уравнению:
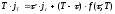 . (49)
. (49)
Решив это уравнение, получим:
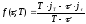 . (50)
. (50)
Пример 14. Пусть на финансовом рынке имеются бескупонные облигации, до погашения которых осталось три месяца и пять месяцев. Номинальная стоимость облигаций – 100 д.е. Рыночная цена облигаций, до погашения которых осталось три месяца – 98,01 д.е., а рыночная цена облигаций до погашения которых осталось пять месяцев – 96,54 д.е. Требуется найти форвардную цену бескупонных облигаций, до погашения которых осталось пять месяцев, на конец третьего месяца.
Решение.
Итак,
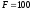 д.е.,
д.е.,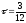 года,
года,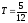 года,
года,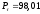 д.е.,
д.е.,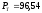 д.е.
д.е.
Вначале
найдем непрерывно капитализируемые
доходности
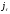 и
и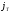 по формуле (22).
по формуле (22).
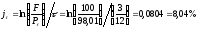 ,
,
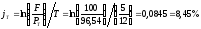 .
.
Найдем
непрерывно капитализируемую форвардную
доходность
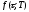 по формуле (50):
по формуле (50):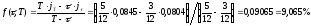 .
.
