
- •1. Общее представление об экономико-математическом моделировании
- •1.1. Определение экономико-математической модели
- •1.2. Классификация экономико-математических моделей
- •1.3. Основные этапы экономико-математического моделирования
- •2. Основы финансовой арифметики
- •2.1. Простой процент
- •Наращенная сумма при простом проценте
- •Текущая стоимость при простом проценте
- •Номинальная годовая процентная ставка
- •3. Математически методы анализа последовательностей платежей
- •3.1. Текущая стоимость последовательности платежей
- •3.2. Будущая стоимость последовательности платежей
- •3.3. Стоимость последовательности платежей в произвольный момент времени
- •4. Моделирование инвестиционных проектов
- •4.1. Дисконтирование денежных потоков инвестиционного проекта
- •4.2. Модель с постоянным процентным ростом свободных денежных потоков
- •4.3. Задача оптимального финансирования проекта
- •4.4. Задача оптимального выбора инвестиционных проектов
- •4.5. Анализ чувствительности денежных потоков проекта
- •4.6. Анализ безубыточности проекта
- •4.7. Влияние инфляции на денежные потоки проекта
- •4.8. Анализ финансового риска инвестиционного проекта
- •4.9. Имитационное моделирование денежных потоков проекта
- •5. Математические методы анализа платежей облигаций
- •5.1. Платежи облигаций
- •5.2. Доходность к погашению облигации
- •5.3. Текущая стоимость облигации
- •5.4. Продолжительность облигации
- •5.5. Чистые доходности
- •5.6. Использование чистых доходностей для оценки рыночной стоимости купонных облигаций
- •5.7. Синтетические бескупонные облигации
- •5.8. Описание оценки рыночной стоимости облигации в общем случае
- •5.9. Условия существования имитирующего портфеля и однозначности оценки рыночной стоимости облигации
- •5.10. «Чистые» коэффициенты дисконтирования, их нахождение и использование для оценки рыночной стоимости облигации
- •5.11. Нахождение чистых доходностей методом наименьших квадратов
- •5.12. Форвардные доходности
- •6. Моделирование процентного риска
- •6.1. Продолжительность и выпуклость портфеля облигаций
- •6.2. Чувствительность текущей стоимости портфеля облигаций к изменению доходности
- •6.3. Чувствительность собственного капитала финансовой организации к изменению доходности облигаций
- •6.4. Иммунизация будущих платежей от процентного риска
- •7. Моделирование кредитного риска
- •7.1. Использование линейной модели вероятности для оценки кредитного риска
- •8. Теория инвестиционного портфеля
- •8.1. Инвестиционный портфель и его основные характеристики
- •8.2. Диверсификация риска
- •8.3. Множество инвестиционных возможностей
- •8.4. Оптимизация инвестиционного портфеля
- •8.5. Множество инвестиционных возможностей при наличии безрисковой доходности
- •8.6. Оптимизация инвестиционного портфеля при наличии безрискового актива
- •8.7. Рыночная модель
- •8.8. Разложение общего риска финансового актива на систематическую и собственную составляющие
- •8.9. Модель оценки финансовых активов
- •9. Математические методы анализа финансовых производных
- •9.1. Основные виды финансовых производных
- •9.2. Рыночная стоимость форвардного контракта
- •9.3. Соотношение между рыночной стоимостью форвардного контракта и форвардной ценой базового актива
- •9.4. Форвардные контракты на покупку валюты
- •9.5. Форвардные контракты на процентные ставки
- •9.6. Фьючерсные контракты
- •9.7. Микрохеджирование с помощью фьючерсных контрактов
- •9.8. Макрохеджирование с помощью фьючерсных контрактов
5.7. Синтетические бескупонные облигации
Часто на финансовом рынке отсутствуют бескупонные облигации заданного качества для заданного срока погашения. Тем не менее методика оценки рыночной стоимости облигаций, описанная выше, может быть использована.
В случае отсутствия бескупонных облигаций под чистыми доходностями понимаются доходности так называемых синтетических бескупонных облигаций. Синтетическая бескупонная облигация – это инвестиционная стратегия, состоящая в приобретении и продаже купонных облигаций, генерирующая только один денежный поток в будущем. Размер этого будущего денежного потока соответствует номиналу бескупонной облигации. А размер денежного потока, генерируемого инвестиционной стратегией в настоящем, (взятый со знаком «плюс») соответствует текущей цене бескупонной облигации.
Пример 11. Пусть на финансовом рынке имеются двухлетние пятипроцентные и пятнадцатипроцентные облигации с номинальными стоимостями 100 д.е. (и с купонным периодом – один год). Цены этих облигаций, соответственно, равны 91,41 д.е. и 108,93 д.е. Требуется построить однолетние и двухлетние синтетические бескупонные облигации с номинальной стоимостью 100 д.е. , найти их цены и соответствующие чистые доходности.
Решение.
Пусть
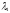 – количество приобретаемых (если
– количество приобретаемых (если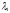 положительно) либо продаваемых (если
положительно) либо продаваемых (если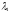 отрицательно) двухлетних пятипроцентных
облигаций, а
отрицательно) двухлетних пятипроцентных
облигаций, а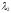 – количество приобретаемых (если
– количество приобретаемых (если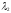 положительно) либо продаваемых (если
положительно) либо продаваемых (если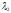 отрицательно) двухлетних
пятнадцатипроцентных облигаций.
отрицательно) двухлетних
пятнадцатипроцентных облигаций.
Очевидно,
что инвестиционная стратегия генерирует
в конце первого года денежный поток,
равный
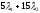 д.е.,
а в конце второго года –
д.е.,
а в конце второго года –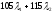 д.е.
д.е.
Для
однолетней синтетической бескупонной
облигации
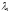 и
и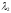 находятся из системы уравнений:
находятся из системы уравнений:
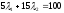 ,
,
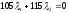 .
.
Решив
эту систему уравнений, получим:
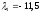 и
и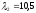 .
Таким образом, однолетняя синтетическая
бескупонная облигация состоит в продаже
11,5 двухлетних пятипроцентных облигаций
и в покупке 10,5 двухлетних пятнадцатипроцентных
облигаций. Цена однолетней синтетической
бескупонной облигации равна:
.
Таким образом, однолетняя синтетическая
бескупонная облигация состоит в продаже
11,5 двухлетних пятипроцентных облигаций
и в покупке 10,5 двухлетних пятнадцатипроцентных
облигаций. Цена однолетней синтетической
бескупонной облигации равна:
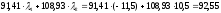 д.е.
д.е.
Теперь мы можем найти чистую доходность для одного года:
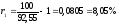 .
.
Для
двухлетней синтетической бескупонной
облигации
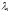 и
и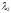 находятся из системы уравнений:
находятся из системы уравнений:
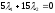 ,
,
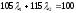 .
.
Решив
эту систему уравнений, получим:
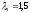 и
и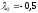 .
Таким образом, двухлетняя синтетическая
бескупонная облигация состоит в покупке
1,5 двухлетних пятипроцентных облигаций
и в продаже 0,5 двухлетней пятнадцатипроцентной
облигации. Цена двухлетней синтетической
бескупонной облигации равна:
.
Таким образом, двухлетняя синтетическая
бескупонная облигация состоит в покупке
1,5 двухлетних пятипроцентных облигаций
и в продаже 0,5 двухлетней пятнадцатипроцентной
облигации. Цена двухлетней синтетической
бескупонной облигации равна:
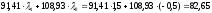 д.е.
д.е.
Найдем чистую доходность для двух лет:
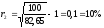 .
.
Чистые доходности можно найти также из системы уравнений, в которой суммы платежей имеющихся на рынке облигаций, дисконтированных с помощью искомых чистых доходностей (соответствующих срокам платежей), приравниваются ценам облигаций. В условиях примера 11 такая система уравнений имеет вид
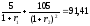 ,
,
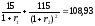 .
.
Решив
эту систему уравнений, получим:
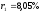 ,
,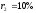 .
.
Заметим, что значения чистых доходностей, полученные в результате решения системы уравнений, совпадают со значениями, полученными с помощью синтетических бескупонных облигаций.
Записанную
выше систему уравнений (относительно
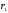 и
и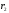 )
удобно свести к системе линейных
уравнений следующим образом. Введем
коэффициенты дисконтирования
)
удобно свести к системе линейных
уравнений следующим образом. Введем
коэффициенты дисконтирования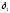 и
и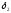 по формулам:
по формулам: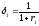 ,
,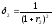 .
Тогда систему уравнений можно записать
в виде:
.
Тогда систему уравнений можно записать
в виде:
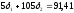 ,
,
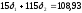 .
.
Решив
эту систему уравнений относительно
коэффициентов дисконтирования
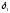 и
и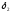 ,
получим:
,
получим: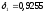 ,
,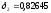 .
Теперь с помощью найденных коэффициентов
дисконтирования
.
Теперь с помощью найденных коэффициентов
дисконтирования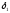 и
и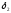 определим чистые доходности
определим чистые доходности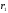 и
и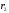 из уравнений:
из уравнений:
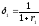 ,
,
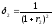 .
.
Получим:
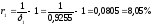 ,
,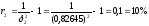 .
.
Используем найденные чистые доходности для дисконтирования платежей двухлетней десятипроцентной облигации (с купонным периодом – один год):
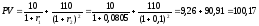 д.е.
д.е.
Покажем,
что полученное значение
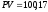 д.е. совпадает с ценой портфеля, состоящего
из двухлетних пятипроцентных и
пятнадцатипроцентных облигаций,
имитирующего платежи данной купонной
облигации.
д.е. совпадает с ценой портфеля, состоящего
из двухлетних пятипроцентных и
пятнадцатипроцентных облигаций,
имитирующего платежи данной купонной
облигации.
Обозначим через
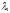 количество двухлетних пятипроцентных
облигаций в портфеле, а через
количество двухлетних пятипроцентных
облигаций в портфеле, а через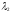 количество двухлетних пятнадцатипроцентных
облигаций в портфеле. Очевидно, что
такой портфель генерирует в конце
первого года денежный поток, равный
количество двухлетних пятнадцатипроцентных
облигаций в портфеле. Очевидно, что
такой портфель генерирует в конце
первого года денежный поток, равный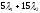 д.е.,
а в конце второго года –
д.е.,
а в конце второго года –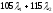 д.е.
Поскольку денежные потоки портфеля
должны совпадать с платежами данной
купонной облигации, должны выполняться
равенства:
д.е.
Поскольку денежные потоки портфеля
должны совпадать с платежами данной
купонной облигации, должны выполняться
равенства:
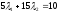 ,
,
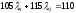 .
.
Решив
эту систему уравнений, получим:
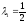 ,
,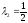 .
Цена такого портфеля равна:
.
Цена такого портфеля равна:
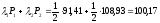 д.е.
д.е.
Итак,
цена портфеля, состоящего из двухлетних
пятипроцентных и пятнадцатипроцентных
облигаций, имитирующего платежи данной
купонной облигации, совпадает с найденным
выше значением
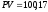 д.е.
д.е.
