
- •1. Общее представление об экономико-математическом моделировании
- •1.1. Определение экономико-математической модели
- •1.2. Классификация экономико-математических моделей
- •1.3. Основные этапы экономико-математического моделирования
- •2. Основы финансовой арифметики
- •2.1. Простой процент
- •Наращенная сумма при простом проценте
- •Текущая стоимость при простом проценте
- •Номинальная годовая процентная ставка
- •3. Математически методы анализа последовательностей платежей
- •3.1. Текущая стоимость последовательности платежей
- •3.2. Будущая стоимость последовательности платежей
- •3.3. Стоимость последовательности платежей в произвольный момент времени
- •4. Моделирование инвестиционных проектов
- •4.1. Дисконтирование денежных потоков инвестиционного проекта
- •4.2. Модель с постоянным процентным ростом свободных денежных потоков
- •4.3. Задача оптимального финансирования проекта
- •4.4. Задача оптимального выбора инвестиционных проектов
- •4.5. Анализ чувствительности денежных потоков проекта
- •4.6. Анализ безубыточности проекта
- •4.7. Влияние инфляции на денежные потоки проекта
- •4.8. Анализ финансового риска инвестиционного проекта
- •4.9. Имитационное моделирование денежных потоков проекта
- •5. Математические методы анализа платежей облигаций
- •5.1. Платежи облигаций
- •5.2. Доходность к погашению облигации
- •5.3. Текущая стоимость облигации
- •5.4. Продолжительность облигации
- •5.5. Чистые доходности
- •5.6. Использование чистых доходностей для оценки рыночной стоимости купонных облигаций
- •5.7. Синтетические бескупонные облигации
- •5.8. Описание оценки рыночной стоимости облигации в общем случае
- •5.9. Условия существования имитирующего портфеля и однозначности оценки рыночной стоимости облигации
- •5.10. «Чистые» коэффициенты дисконтирования, их нахождение и использование для оценки рыночной стоимости облигации
- •5.11. Нахождение чистых доходностей методом наименьших квадратов
- •5.12. Форвардные доходности
- •6. Моделирование процентного риска
- •6.1. Продолжительность и выпуклость портфеля облигаций
- •6.2. Чувствительность текущей стоимости портфеля облигаций к изменению доходности
- •6.3. Чувствительность собственного капитала финансовой организации к изменению доходности облигаций
- •6.4. Иммунизация будущих платежей от процентного риска
- •7. Моделирование кредитного риска
- •7.1. Использование линейной модели вероятности для оценки кредитного риска
- •8. Теория инвестиционного портфеля
- •8.1. Инвестиционный портфель и его основные характеристики
- •8.2. Диверсификация риска
- •8.3. Множество инвестиционных возможностей
- •8.4. Оптимизация инвестиционного портфеля
- •8.5. Множество инвестиционных возможностей при наличии безрисковой доходности
- •8.6. Оптимизация инвестиционного портфеля при наличии безрискового актива
- •8.7. Рыночная модель
- •8.8. Разложение общего риска финансового актива на систематическую и собственную составляющие
- •8.9. Модель оценки финансовых активов
- •9. Математические методы анализа финансовых производных
- •9.1. Основные виды финансовых производных
- •9.2. Рыночная стоимость форвардного контракта
- •9.3. Соотношение между рыночной стоимостью форвардного контракта и форвардной ценой базового актива
- •9.4. Форвардные контракты на покупку валюты
- •9.5. Форвардные контракты на процентные ставки
- •9.6. Фьючерсные контракты
- •9.7. Микрохеджирование с помощью фьючерсных контрактов
- •9.8. Макрохеджирование с помощью фьючерсных контрактов
5.5. Чистые доходности
В
финансовом анализе важную роль играют
так называемые чистые доходности (англ.
pure
yield).
Чистая доходность – это доходность к
погашению бескупонной облигации ,т.е.
облигации, не выплачивающей купонные
платежи ( ).
Чистые доходности играют важную роль
для оценки рыночной стоимости облигаций.
).
Чистые доходности играют важную роль
для оценки рыночной стоимости облигаций.
Поскольку
в случае бескупонной облигации
 ,
уравнение (4) принимает вид:
,
уравнение (4) принимает вид:
 . (17)
. (17)
Решив это уравнение, получим следующую формулу для нахождения чистой доходности:
 . (18)
. (18)
Отметим, что чистая доходность, найденная по формуле (18) – это эффективная доходность для заданного промежутка времени.
Пример 8. Пусть рыночные цены однолетней и двухлетней бескупонных облигаций с номинальными стоимостями 100 д.е. равны, соответственно, 90,45 д.е. и 78,24 д.е. Требуется найти эффективные годовые чистые доходности для одного года и для двух лет.
Решение.
Итак,
 ,
д.е.,
,
д.е., д.е.,
д.е., д.е.
(где
д.е.
(где – цена однолетней бескупонной облигации,
– цена однолетней бескупонной облигации, – цена двухлетней бескупонной облигации).
Обозначим через
– цена двухлетней бескупонной облигации).
Обозначим через чистую доходность для одного года, а
через
чистую доходность для одного года, а
через чистую доходность для двух лет. Для
нахождения
чистую доходность для двух лет. Для
нахождения и
и воспользуемся формулой (18).
воспользуемся формулой (18).
 ,
,
 .
.
В случае, когда срок до погашения бескупонной облигации состоит из нецелого числа периодов времени, уравнение (17) имеет вид:
 . (19)
. (19)
Решив это уравнение, получим:
 . (20)
. (20)
Пример 9. Пусть рыночная цена бескупонной облигации с номинальной стоимостью 100 д.е., до погашения которой остался один месяц, равна 99,32 д.е. Требуется найти эффективную годовую чистую доходность для одного месяца.
Решение.
Итак,
 д.е.,
д.е., д.е.,
д.е., года. Для нахождения чистой доходности
воспользуемся формулой (20):
года. Для нахождения чистой доходности
воспользуемся формулой (20):
 .
.
 означает,
что вложение денег в бескупонные
облигации, до погашения которых остался
один месяц, эквивалентно вложению денег
в банк на один месяц при эффективной
годовой процентной ставке 8,53%.
означает,
что вложение денег в бескупонные
облигации, до погашения которых остался
один месяц, эквивалентно вложению денег
в банк на один месяц при эффективной
годовой процентной ставке 8,53%.
Обозначим
через
 чистую доходность для срокаt.
Последовательность чистых доходностей
чистую доходность для срокаt.
Последовательность чистых доходностей
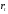 (при разных срокахt)
называют временной структурой чистых
доходностей.
(при разных срокахt)
называют временной структурой чистых
доходностей.
Поскольку временную структуру чистых доходностей удобно изображать графически, временную структуру чистых доходностей часто называют кривой чистых доходностей.
Кривая чистых доходностей:
rt


t

В случае, когда чистые доходности постоянны (т.е. не зависят от срока t), говорят, что временная структура чистых доходностей – плоская.
Отметим, что часто бывает удобно пользоваться непрерывно капитализируемыми чистыми доходностями. Такая доходность (обозначаемая в дальнейшем j) в соответствии с формулой (22) главы 1 определяется уравнением:
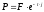 . (21)
. (21)
Решив это уравнение, получим:
 . (22)
. (22)
Пример 10. В условиях примера 9 требуется найти непрерывно капитализируемую чистую доходность.
Решение.
Итак,
 д.е.,
д.е., д.е.,
д.е., года. Для нахождения непрерывно
капитализируемой чистой доходности
воспользуемся формулой (22).
года. Для нахождения непрерывно
капитализируемой чистой доходности
воспользуемся формулой (22).
 .
.
5.6. Использование чистых доходностей для оценки рыночной стоимости купонных облигаций
Покажем,
как используются чистые доходности для
дисконтирования платежей облигаций. В
результате решения задачи примера 8 мы
нашли чистые доходности для одного года
и для двух лет:
 ,
, .
Используем эти чистые доходности для
дисконтирования платежей двухлетней
десятипроцентной облигации (с купонным
периодом – один год). Платежи двухлетней
десятипроцентной облигации с номинальной
стоимостью 100 д.е. (и с купонным периодом
– один год) равны 10 д.е. в конце первого
года и 110 д.е. в конце второго года. Для
дисконтирования платежей купонной
облигации используются чистые доходности,
соответствующие срокам платежей. Таким
образом,
.
Используем эти чистые доходности для
дисконтирования платежей двухлетней
десятипроцентной облигации (с купонным
периодом – один год). Платежи двухлетней
десятипроцентной облигации с номинальной
стоимостью 100 д.е. (и с купонным периодом
– один год) равны 10 д.е. в конце первого
года и 110 д.е. в конце второго года. Для
дисконтирования платежей купонной
облигации используются чистые доходности,
соответствующие срокам платежей. Таким
образом,
 д.е.
д.е.
Покажем,
что полученное значение
 д.е. совпадает с ценой портфеля, состоящего
из однолетних и двухлетних бескупонных
облигаций, имитирующего платежи данной
купонной облигации.
д.е. совпадает с ценой портфеля, состоящего
из однолетних и двухлетних бескупонных
облигаций, имитирующего платежи данной
купонной облигации.
Обозначим
через
 количество однолетних бескупонных
облигаций в портфеле, а через
количество однолетних бескупонных
облигаций в портфеле, а через количество двухлетних бескупонных
облигаций в портфеле. Очевидно, что
такой портфель генерирует в конце
первого года денежный поток, равный
количество двухлетних бескупонных
облигаций в портфеле. Очевидно, что
такой портфель генерирует в конце
первого года денежный поток, равный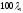 д.е., а в конце второго года –
д.е., а в конце второго года – д.е.
д.е.
Поскольку денежные потоки портфеля должны совпадать с платежами данной купонной облигации, должны выполняться равенства:
 ,
,
 .
.
Из
этих уравнений получаем:
 ,
, .
Таким образом, портфель, имитирующий
платежи данной купонной облигации,
должен состоять из
.
Таким образом, портфель, имитирующий
платежи данной купонной облигации,
должен состоять из однолетней бескупонной облигации и
однолетней бескупонной облигации и двухлетних бескупонных облигаций. Цена
такого портфеля равна
двухлетних бескупонных облигаций. Цена
такого портфеля равна
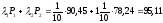 д.е.
д.е.
Замечание.
Мы получили нецелые количества бескупонных
облигаций в имитирующем портфеле:
 ,
, ,
и затем использовали эти нецелые
количества для нахождения цены портфеля.
На практике, нельзя приобрести дробную
часть облигации.
,
и затем использовали эти нецелые
количества для нахождения цены портфеля.
На практике, нельзя приобрести дробную
часть облигации. и
и означает, что портфель, состоящий из
одной однолетней бескупонной облигации
и 11 двухлетних бескупонных облигаций
генерирует такие же денежные потоки
как у 10 двухлетних купонных облигаций.
означает, что портфель, состоящий из
одной однолетней бескупонной облигации
и 11 двухлетних бескупонных облигаций
генерирует такие же денежные потоки
как у 10 двухлетних купонных облигаций.
Итак, цена портфеля, состоящего из однолетних и двухлетних бескупонных облигаций, имитирующего платежи данной купонной облигации, совпадает с текущей стоимостью купонной облигации, найденной с помощью чистых доходностей. Оказывается, это не случайное совпадение. В дальнейшем мы покажем, что (при выполнении некоторых естественных условий) текущая стоимость купонной облигации (найденная с помощью чистых доходностей) всегда совпадает с ценой имитирующего портфеля.
Очевидно, что на эффективном финансовом рынке цена такого портфеля должна совпадать с ценой купонной облигации.
