- •1. Общее представление об экономико-математическом моделировании
- •1.1. Определение экономико-математической модели
- •1.2. Классификация экономико-математических моделей
- •1.3. Основные этапы экономико-математического моделирования
- •2. Основы финансовой арифметики
- •2.1. Простой процент
- •Наращенная сумма при простом проценте
- •Текущая стоимость при простом проценте
- •Номинальная годовая процентная ставка
- •3. Математически методы анализа последовательностей платежей
- •3.1. Текущая стоимость последовательности платежей
- •3.2. Будущая стоимость последовательности платежей
- •3.3. Стоимость последовательности платежей в произвольный момент времени
- •4. Моделирование инвестиционных проектов
- •4.1. Дисконтирование денежных потоков инвестиционного проекта
- •4.2. Модель с постоянным процентным ростом свободных денежных потоков
- •4.3. Задача оптимального финансирования проекта
- •4.4. Задача оптимального выбора инвестиционных проектов
- •4.5. Анализ чувствительности денежных потоков проекта
- •4.6. Анализ безубыточности проекта
- •4.7. Влияние инфляции на денежные потоки проекта
- •4.8. Анализ финансового риска инвестиционного проекта
- •4.9. Имитационное моделирование денежных потоков проекта
- •5. Математические методы анализа платежей облигаций
- •5.1. Платежи облигаций
- •5.2. Доходность к погашению облигации
- •5.3. Текущая стоимость облигации
- •5.4. Продолжительность облигации
- •5.5. Чистые доходности
- •5.6. Использование чистых доходностей для оценки рыночной стоимости купонных облигаций
- •5.7. Синтетические бескупонные облигации
- •5.8. Описание оценки рыночной стоимости облигации в общем случае
- •5.9. Условия существования имитирующего портфеля и однозначности оценки рыночной стоимости облигации
- •5.10. «Чистые» коэффициенты дисконтирования, их нахождение и использование для оценки рыночной стоимости облигации
- •5.11. Нахождение чистых доходностей методом наименьших квадратов
- •5.12. Форвардные доходности
- •6. Моделирование процентного риска
- •6.1. Продолжительность и выпуклость портфеля облигаций
- •6.2. Чувствительность текущей стоимости портфеля облигаций к изменению доходности
- •6.3. Чувствительность собственного капитала финансовой организации к изменению доходности облигаций
- •6.4. Иммунизация будущих платежей от процентного риска
- •7. Моделирование кредитного риска
- •7.1. Использование линейной модели вероятности для оценки кредитного риска
- •8. Теория инвестиционного портфеля
- •8.1. Инвестиционный портфель и его основные характеристики
- •8.2. Диверсификация риска
- •8.3. Множество инвестиционных возможностей
- •8.4. Оптимизация инвестиционного портфеля
- •8.5. Множество инвестиционных возможностей при наличии безрисковой доходности
- •8.6. Оптимизация инвестиционного портфеля при наличии безрискового актива
- •8.7. Рыночная модель
- •8.8. Разложение общего риска финансового актива на систематическую и собственную составляющие
- •8.9. Модель оценки финансовых активов
- •9. Математические методы анализа финансовых производных
- •9.1. Основные виды финансовых производных
- •9.2. Рыночная стоимость форвардного контракта
- •9.3. Соотношение между рыночной стоимостью форвардного контракта и форвардной ценой базового актива
- •9.4. Форвардные контракты на покупку валюты
- •9.5. Форвардные контракты на процентные ставки
- •9.6. Фьючерсные контракты
- •9.7. Микрохеджирование с помощью фьючерсных контрактов
- •9.8. Макрохеджирование с помощью фьючерсных контрактов
4.7. Влияние инфляции на денежные потоки проекта
В данном параграфе будет исследовано влияние инфляции на денежные потоки, чистую текущую стоимость и внутреннюю доходность проекта.
Уровень
инфляции за некоторый период времени
определяется следующим образом. Пусть
потребительская корзина состоит из m
видов благ (т.е. товаров и услуг). Обозначим
через
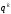 количество
единицk-го
блага в потребительской корзине, через
количество
единицk-го
блага в потребительской корзине, через
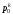 –
рыночную цену единицыk-го
блага в начале периода времени и через
–
рыночную цену единицыk-го
блага в начале периода времени и через
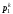 –
рыночную цену единицыk-го
блага в конце периода. Очевидно, что
цены
–
рыночную цену единицыk-го
блага в конце периода. Очевидно, что
цены
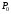 и
и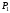 потребительской корзины в начале и в
конце периода времени равны, соответственно:
потребительской корзины в начале и в
конце периода времени равны, соответственно:
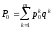 и
(77)
и
(77)
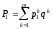 .
(78)
.
(78)
Уровень инфляции i за период времени определяется по формуле:
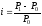 .
(79)
.
(79)
Пример 13. Пусть потребительская корзина состоит из трех яблок и двух апельсин. Цена яблока составляла четыре денежных единицы в начале года и за год возросла до шести денежных единиц. Цена апельсина составляла девять денежных единиц в начале года и за год увеличилась до двенадцати денежных единиц. Определить годовой уровень инфляции.
Решение.
В данном примере потребительская корзина
состоит из благ двух видов – яблок и
апельсин. Пусть индекс
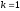 соответствует яблокам, а
соответствует яблокам, а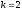 –
апельсинам. Тогда
–
апельсинам. Тогда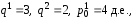
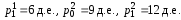 ,
и цены потребительской корзины в начале
и в конце года равны, соответственно:
,
и цены потребительской корзины в начале
и в конце года равны, соответственно:
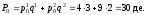 ,
,
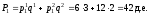
Теперь можно найти годовой уровень инфляции:
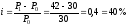 .
.
Пусть
r
– эффективная банковская процентная
ставка за период времени. Тогда сумма
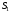 ,
наращенная за период времени при
начальном капитале
,
наращенная за период времени при
начальном капитале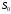 ,
равна:
,
равна:
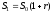 .
(80)
.
(80)
В дальнейшем процентную ставку r будем называть номинальной.
Очевидно,
что в начале периода за начальный капитал
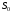 можно
купить
можно
купить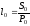 потребительских корзин. В конце периода
за наращенную сумму
потребительских корзин. В конце периода
за наращенную сумму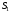 можно
купить
можно
купить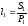 потребительских корзин. Реальная
процентная ставка
потребительских корзин. Реальная
процентная ставка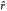 определяется по формуле:
определяется по формуле:
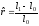 (81)
(81)
и показывает на сколько процентов больше потребительских корзин можно купить в конце периода за наращенную сумму, чем в начале периода за начальный капитал.
Реальная процентная ставка учитывает инфляцию в отличие от номинальной процентной ставки.
Найдем взаимосвязь между реальной процентной ставкой, номинальной процентной ставкой и уровнем инфляции. Из приведенных выше формул следует, что
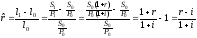 .
(82)
.
(82)
Итак, реальная процентная ставка определяется с помощью номинальной процентной ставки и уровня инфляции по формуле:
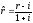 .
(83)
.
(83)
Пример 14. Пусть годовая номинальная процентная ставка равна 45%, а годовой уровень инфляции составляет 40 %. Найти реальную процентную ставку.
Решение.
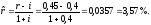
Покажем как можно учесть инфляцию при анализе проекта, рассмотренного в двух предыдущих параграфах.
Можно
считать, что при годовом уровне инфляции
i
цена pk
единицы продукции в конце k-го
года равняется
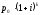 ,
где
,
где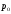 – цена единицы продукции в начальный
момент времени. Например, если
– цена единицы продукции в начальный
момент времени. Например, если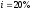 и
и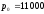 д.е., то цена автомобиля в конце третьего
года составит
д.е., то цена автомобиля в конце третьего
года составит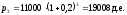 Аналогичным образом увеличатся переменные
и постоянные издержки, и денежный поток
вk-м
году будет вычисляться по формуле
Аналогичным образом увеличатся переменные
и постоянные издержки, и денежный поток
вk-м
году будет вычисляться по формуле
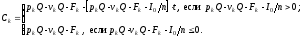 (84)
(84)
Считая,
что годовой уровень инфляции равен 20%,
и в начальный момент времени цена единицы
продукции, удельные переменные издержки
и постоянные издержки соответствуют
значениям, приведенным в примере 7 (т.е.
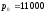 д.е. ,
д.е. ,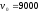 д.е. и
д.е. и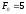 млн. д.е.), по формуле (84) можно определить
годовые свободные денежные потоки с
первого по пятый годы:C1
= 14000 тыс. д.е., C2
= 16160 тыс. д.е., C3
= 18752 тыс. д.е., C4
= 21862 тыс. д.е., C5
= 25595 тыс. д.е.
млн. д.е.), по формуле (84) можно определить
годовые свободные денежные потоки с
первого по пятый годы:C1
= 14000 тыс. д.е., C2
= 16160 тыс. д.е., C3
= 18752 тыс. д.е., C4
= 21862 тыс. д.е., C5
= 25595 тыс. д.е.
В этом случае временная диаграмма денежных потоков проекта выглядит следующим образом:
Денежные
потоки -40000 14000 16160 18752 21862
25595 
(в
тыс. д.е.)





Годы 0 1 2 3 4 5
Определим внутреннюю норму прибыли проекта. Уравнение (4) в данном случае имеет вид
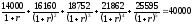 .
.
Решив это уравнение (например, с помощью встроенной финансовой функции ВНДОХ табличного процессора Excel), получим IRR = 33,93%.
IRR = 33,93% – это номинальная внутренняя доходность проекта. Реальная внутренняя норма прибыли проекта находится по формуле (83):
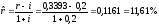 .
.
Отметим, что при нахождении чистой текущей величины проекта также учитывается инфляция. А именно, инфляция влияет на внутреннюю доходность альтернативных проектов (вспомним, что внутренняя доходность альтернативных проектов используется в качестве ставки дисконтирования денежных потоков проекта).
Из формулы (83) следует, что номинальная процентная ставка находится с помощью реальной процентной ставки и уровня инфляции следующим образом:
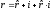 .
(85)
.
(85)
Эту
формулу можно использовать для определения
ставки дисконтирования свободных
денежных потоков проекта. Например,
если реальная (т.е. без учета инфляции)
доходность альтернативных проектов
равна 14%, а годовой уровень инфляции –
20%, то ставка дисконтирования равна
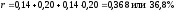 ,
и чистая текущая стоимость проекта
составит
,
и чистая текущая стоимость проекта
составит