1.Матрица – прямоугольная таблица чисел, содержащая m строк одинаковой длины(или n столбцов одинаковой длины).

a11 a12 … an1

A= a21 a22 … an2

… … … …

am 1 am2 … amn

a1i a2i …ain-i=1,m – i-тая строка

a1j a2j … amj-j= 1,n – j-тый столбец

Элементы, стоящие по диагонали, идущей из верхнего левого угла, образуют главную диагональ; из верхнего правого – побочную.

Матрицы равны между собой, если равны их соответствующие элементы.

Матрица, у которой число строк равно числу столбцов, называется квадратной.

Матрица размера n·n - матрица n-го порядка.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю – диагональная.

Диагональная матрица у которой каждый элемент главной диагонали равен единице, единичная.

Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.

Матрица, все элементы которой равны нулю, - нулевая.( обозначается буквой О)

Матрица, содержащая один столбец или одну строку – вектор.

2.Умножение матрицы на число

Пусть задана матрица А=aij i=1,m; j=1,n; α принадлежит R. Чтобы умножить матрицу А на число α, нужно кадый Эл-т матрицы умножить на это число α .

С=(αaij)

Сложение матриц

Пусть заданы А=aij и В=bij одинаковой размерности i=1,m; j=1,n. Тогда суммой двух этих матриц называется матрица С=сij. Другими словами, нужно сложить соответствующие эл-ты. Кратко: С=А+В

Св-ва:

1. А+В=В+А

2. А+(В+С)=(А+В)+С

3. А+0=А

4. А-А=0

5. 1·А=А

6. α·(А+В)=αА+αВ

7. (α+β)·А=αА+βА

8. α·(βА)=(βα)·А

3.Умножение матриц

2 Матр а и в соглас-е, если число строк матр а равно числу столбцов матр в, и наоборот.

Оп-ция умн-я матриц определена только для соглас. матриц.

Кв матрицы одного и того же порядка и одной и той же размерности всегда согласованны.

Пусть задана матр А=aik i=1,m; k=1,n и матр В=bkj k=1,m; j=1,n. Тогда произв-ем А на В наз. матр С такая, что сik=ai1·b1k+ ai2·b2k +…+ ain·bnk, где i=1,m; k=1,n, т.е. эл-т i-той строки и k-того столбца матрицы произв-ия С равен ∑ произв-ий эл-ов i-той строки матр А на соответствующие эл-ты k-того столбца матр В.

Если выполняется равенство АВ=ВА, то матрицы А и В наз. перестановочными (коммутирующими)

Матр,получ. из данной заменой кажд ее строки столбц с тем же номером,наз. транспон-ой к данной.

Св-ва умножения:

1.А·(ВС)=(АВ)С

2. А(В+С)=АВ+ВС

3. (А+В)С=АС+ВС

4. α(АВ)=(αА)В

Св-ва транспонирования:

1.(А+В)^т=А^т+В^т

2. (АВ)^т=В·А^т

3. (А^т) ^т= А

Квадратная матрица А, которая не меняется при транспонировании, - симметричная.

Если матрица симметрична, то эл-ты, равноудаленные от главной диагонали, совпадают.

А= 2 5 -2

5 -7 3

-2 3 1

4.Опред-ль 1,2,3 порядков.

Квадратной матрице А порядка n можно сопоставить число det A, называемое ее определителем следующим образом:

1. n=1. A=(a₁); det A=a₁

2. n=2.

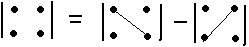
3. n=3.

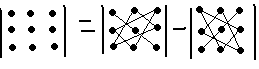
5.Свойства определителей.

1) Если к.-л. строка или столбец в матрице состоит из одних нолей, то det

этой матрицы равен 0

2)При транспонировании матрицы её определитель не изменяется: (detА =detА')

3) При перестановке местами 2-х строк или столбцов матрицы её

определитель меняет свой знак на противоположный

4) Если квадратная матрица содержит 2 одинаковых строки или столбца, то её определитель равен 0.

5)Если 2 строки или 2 столбца матрицы пропорциональны, то её det равен 0.

6) Определитель матрицы не изменяется если к элементам одной строки (или столбца) прибавить элементы другой строки (или столбца), умноженные на одно и то же число

7) Общий множитель строки или столбца можно выносить за знак определителя

8) Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель можно представить в виде суммы 2-х определителей по формуле, например,

Доказательство – проверкой.

9) det верхней треуг. матрицы = произведению диагональных эл-тов.

10) det A*B=detA*detB

6.Обратная матрица

Обр матр — такая матр A^-1, при умн-и на кот исходная матрица A даёт в результате единичную матрицу E:

AA⁻¹ = A⁻¹A = E

Теорема : для того, чтобы для кв.м.А сущ-ла обр, дост-но чтобы опр-ль этой м. был отличен от 0.(Кв матр обратима тогда и только тогда, когда она невырожденная, т.е. её опр-ль не равен 0. Для некв матриц обр матриц не сущ-т.)

Доказательство:

Необходимость. Пусть для матрицы A существует обратная матрица A^-1.

detA^-1*A=detE => detA≠ 0.

Достаточность.

по м.А строим А^*

где А^* - м. алгебраических дополнений А^*

транспонируем полученную матрицу: (А^*)^Т=

найдем А* (А^*)^Т=С, Заметим, что все диагональные элементы матрицы C будут равны 1. Действительно, например,

следовательно А* (А^*)^Т=detA*E => =>

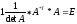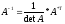
Сформ-м правило нах-я обр матр на примере матр А.