Тема 1 вступ в опір матеріалів

1.1. Три задачі опору матеріалів

Опір матеріалів є загальноінженерною дисципліною, що вирішує три задачі:

1. Викладення методів розрахунку конструкцій на міцність. Міцність  здатність елементів конструкцій і деталей машин чинити опір зовнішнім навантаженням, не руйнуючись.

2. Викладення методів розрахунку елементів конструкцій і деталей машин на жорсткість. Жорсткість  здатність елементів конструкцій і деталей машин чинити опір зовнішнім навантаженням без суттєвих деформацій. Деформація  зміна форми і розмірів конструкції при дії навантаження.

3. Викладення методів розрахунку стиснутих елементів конструкцій і деталей машин на стійкість. Стійкість  здатність конструкції та її елементів зберігати певну початкову форму пружної рівноваги.

1.2. Розрахункова схема. Три групи схематизації

Розрахунковою схемою конструкції є реальний об'єкт, позбавлений несуттєвих особливостей з погляду опору матеріалів. До числа суттєвих факторів розрахункової схеми відносять: геометрію об'єкта, його форму і розміри; фізичні характеристики матеріалу; навантаження, що прикладаються до об'єкта.

Відповідно до наявності основних факторів розрахункової схеми розрізняють три групи схематизації:

1. Схематизація геометрії об'єкта

За своєю геометрією всі об'єкти можуть бути розділені на наступні типи:

а) Брус (Рис.1.1,а) і стержень (Рис.1.1,б) ( елементи кронструкції, у яких два поперчних розміри істотно менші за третій (довжину).

Рис.1.1

б) Пластинка (Рис. 1.2,а) і оболонка (Рис.1.2,б) ( елемент конструкції, у якого два розміри істотно менші за третій (товщину);

Рис.1.2

в) Масив (Рис.1.3) або тривимірне тіло (усі три розміри елемента конструкції порівняні за величиною).

Рис.1.3

2. Схематизація фізичних властивостей матеріалу

В опорі матеріалів приймають наступні гіпотези:

а) гіпотеза суцільності матеріалу;

б) гіпотеза однорідності матеріалу;

в) гіпотеза про абсолютну пружність матеріалу (гіпотеза лінійної деформівності);

г) гіпотеза про ізотропність матеріалу;

д) гіпотеза про природну ненапруженість.

3. Схематизація навантажень

Відповідно до цієї групи схематизації розрізняють такі навантаження:

а) зосереджена сила;

б) зосереджена пара сил;

в) розподілене навантаження заданої інтенсивності;

г) розподілений момент заданої інтенсивності.

1.3. Метод перерізів. Внутрішні силові фактори

На відміну від теоретичної механіки опір матеріалів оперує з деформованими тілами. Отже, однією з задач опору матеріалів є визначення внутрішніх сил, що виникають в конструкції, навантаженої зовнішніми силами.

Для визначення внутрішніх зусиль в опорі матеріалів застосовують метод перерізів. Розглянемо довільне тіло, що зазнає дії зовнішніх сил у вигляді активних і реактивних сил і знаходиться у стані рівноваги (Рис.1.4).

Рис.1.4

Розсічемо думкою це тіло перерізом перпендикулярним до поздовжньої осі тіла і розглянемо кожну з частин тіла окремо (Рис.1.5).

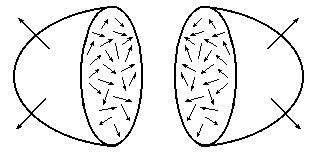
Рис.1.5

В перерізі ми виявимо безліч довільно спрямованих у просторі сил взаємодії між частками тіла. Безпосередньо урахувати всі ці сили при визначенні внутрішніх силових факторів, що діють в перерізі, неможливо. Тому скористаємося теоремою про зведення просторової системи сил до довільного центру. Виберемо в якості такого центру центр ваги перерізу і замінимо всі сили, що діють в перерізі головним вектором, прикладеним в центрі зведення , і головним моментом системи сил відносно цього центру. Головний вектор і головний момент системи сил, що діють на ліву частину тіла, позначимо відповідно і (Рис.1.6). Головний вектор і головний момент системи сил, що діють на праву частину тіла, позначимо через і . Кожна з цих пар сил щодо частини тіла, до якої вони прикладені, є силами зовнішніми і одночасно для всього тіла в цілому ці сили є силами внутрішніми. За третім законом Ньютона про дію і рівну протидію , .

Рис.1.6

Зведемо тепер до головного вектора і головного моменту зовнішні сили, що діють на кожну з частин тіла, і позначимо їх так: і  головний вектор і головний момент зовнішніх сил, що прикладені до лівої частини тіла; і  головний вектор і головний момент зовнішніх сил, що діють на праву частину тіла (Рис.1.6). Центром зведення вважатимемо центр ваги перерізу.

Під дією зовнішніх і внутрішніх сил кожна з частин тіла буде перебувати у стані рівноваги. Умови рівноваги виглядатимуть для лівої частини тіла так: , ; для правої частини тіла: , . Зважаючи на те, що , , маємо: ; . І навпаки: ; .

Таким чином, скориставшись методом перерізів, отримуємо наступне правило для визначення головного вектора і головного моменту всіх сил, що діють у перерізі: головний вектор і головний момент усіх внутрішніх сил, що діють у розглянутому перерізі на частину тіла, що залишилася, дорівнюють відповідно головному векторові і головному моментові всіх зовнішніх сил, що прикладені до відкинутої частини тіла.

Головний вектор і головний момент усіх внутрішніх сил можна розкласти на складові. Складовими головного вектора є: поздовжня сила  проекція головного вектора на вісь ;  проекції поперечної сили на осі , що лежать у площині поперечного перерізу (Рис.1.7). Складовими головного моменту усіх внутрішніх сил є: згинальні моменти відносно осей , крутний момент  проекція головного моменту на вісь (Рис.1.7).

Рис.1.7

Таким чином, усього існує шість внутрішніх силових факторів, для визначення яких у теоретичній механіці (Розділ “Статика”) існують шість рівнянь рівноваги.

Серед усіляких видів деформації розрізняють чотири види простої деформації:

1.Осьове розтягання та стискання (Рис.1.8)  з усіх внутрішніх силових факторів відмінною від нуля є тільки поздовжня сила ( ).

Рис.1.8

2. Зсув (Рис.1.9)  з усіх внутрішніх силових факторів відмінними від нуля є проекції поперечної сили ( або ).

Рис.1.9

3. Кручення (Рис.1.10)  з усіх внутрішніх силових факторів відмінним від нуля є тільки крутний момент ( ).

Рис.1.10

4. Плоске поперечне згинання (Рис.1.11)  з усіх внутрішніх силових факторів відмінними від нуля є проекція поперечної сили і проекція згинального моменту .

Рис.1.11

1.4.Напруження у точці. Інтегральні залежності між внутрішніми силовими факторами і напруженнями у точці

Напруженням у точці називається міра інтенсивності внутрішніх сил:

, (1.1)

де  повне напруження у точці;  частина головного вектора , що припадає на площу поперечного перерізу .

Вектор повного напруження у точці можна розкласти на складові: нормальне напруження  проекцію повного вектора напруження на нормаль до перерізу; дотичне напруження  проекцію повного вектора напруження на площину поперечного перерізу. Тут  проекції вектора дотичного напруження відповідно на осі і .

Між внутрішніми силовими факторами і напруженнями існують інтегральні залежності (Рис.1.12):

; (1.2)

; (1.3)

; (1.4)

; (1.5)

; (1.6)

. (1.7)

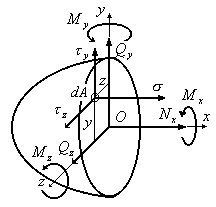
Рис.1.12

Наведені інтегральні залежності встановлюють лише якісний зв'язок між напруженнями і внутрішніми зусиллями. Визначити напруження, що входять у вирази (1.2)(1.7), можна лише у тому випадку, якщо буде відомий закон розподілу напружень по площі поперечного перерізу.