Тема 2 осьове розтягання та стикання

2.1. Визначення поздовжньої сили

При осьовому розтяганні та стисканні виникає єдиний внутрішній силовий фактор  поздовжня сила . Для визначення величини поздовжньої сили використовується метод перерізів. Розсікаючи стержень перерізом (Рис.2.1,а) і розглядаючи рівновагу відсіченої частини (Рис.2.1,б), маємо наступне правило: величина поздовжньої сили чисельно дорівнює алгебраїчній сумі проекцій на поздовжню вісь стержня всіх зовнішніх сил, що діють з одного боку від розглядуваного перерізу.

Рис.2.1

Знак поздовжньої сили буде додатним, якщо поздовжня сила діє від перерізу (Рис.2.2,а), і від’ємним, якщо поздовжня сила діє до перерізу.

а) б)

Рис.2.2

Проілюструємо це правило на прикладі.

Приклад 2.1. Визначити величину поздовжньої сили на кожній з ділянок стержня, зображеного на рис.2.3,а. Побудувати діаграму розподілення поздовжніх зусиль уздовж стержня. Впливом власної ваги стержня знехтувати.

Рішення:

1. Випливаючи з викладеного вище правила, поздовжню силу на ділянці 1 знайдемо, сумуючи проекції на поздовжню вісь стержня всі зовнішні сили, що діють з одного боку від перерізу I-I:

40кН

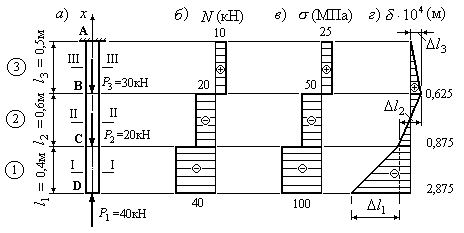
Рис.2.3

2. На другій ділянці величина поздовжньої сили дорівнює:

40+20=20кН

3. На третій ділянці стрержня поздовжня сила дорівнюватиме:

40+20+30=10кН

У кожнім з розглянутих випадків знак поздовжнього зусилля визначається напрямком зовнішньої сили: від перерізу  “+”, до перерізу  “”.

На рис.2.3,б наведена діаграма розподілення поздовжньої сили уздовж стержня.

2.2. Нормальні напруження при осьовому розтяганні та стисканні

При осьовому розтяганні та стисканні поздовжня сила і нормальні напруження зв'язані наступної интегральною залежністю:

. (2.1)

Щоб визначити за допомогою цієї формули нормальне напруження , необхідно знати закон розподілу нормальних напружень по площі поперечного перерізу при осьовому розтяганні та стисканні. Такий закон встановлюється гіпотезою плоских перерізів (гіпотезою Бернуллі):перерізи, що були плоскими до деформації залишаються плоскими в процесі деформації.

З цієї гіпотези випливає, що нормальні напруження, що діють у поперечних перерізах стержня при осьовому розтяганні та стисканні, є величиною сталою (). Роз’язуючи інтеграл (2.1) при сталому значенні нормальних напружень, отримуємо наступний вираз для поздовжньої сили:

, (2.2)

звідки:

. (2.3)

Напруження визначаються в системі одиниць SI у (Па).

Розглянемо приклад визначення напружень у поперечних перерізах стержня, наведеного на рис.2.3.

Приклад 2.2. Знайти величину нормальних напружень на кожній ділянці стержня, наведеного на рис.2.3,а, якщо площа поперечного перерізу уздовж всього стержня стала і дорівнює см². Побудувати діаграму розподілення нормальних напружень уздовж стержня. Впливом власної ваги стержня знехтувати.

Рішення:

1. Скористаємося виразом (2.3) і визначимо напруження на першій ділянці стержня:

100 МПа

2. На другій ділянці нормальне напруження знайдемо з виразу:

50 МПа

3. На третій ділянці:

25МПа

4. На рис.2.3,в наведена діаграма розподілення нормальных напружень уздовж стержня.