12.9. Кручення з розтяганням. Загальний випадок згинання, розтягання і кручення
При
цьому виді складного опору також виникає
в небезпечних точках перерізу елементів
конструкцій складний напружений стан.
У зв'язку з цим цей вид деформації можна
також віднести до другої групи видів
складного опору. Так само, як і при
згинанні з крученням оцінку міцності
виконують з застосуванням теорій
міцності. Однак, на відміну від згинання
з крученням при крученні з розтяганням
зведений момент не обчислюють, тому що
нормальні напруження, що виникають у
перерізі елемента конструкції,
обчислюються за іншою формулою (
).
У зв'язку з цим трохи змінюється методика
визначення розрахункових напружень.
Так само, як при згинанні з крученням,
складний вид деформації розкладається
на два простих – розтягання і кручення.
Для кожного з цих видів деформації
будуються епюри розподілу внутрішніх
силових факторів, відшукується небезпечний
переріз і для небезпечних точок перерізу
знаходяться нормальні і дотичні
напруження від кожного внутрішнього
силового фактора окремо і підставляютьсябезпосередньо
у вираз для розрахункових напружень.
Наприклад, при використанні теорії
найбільших дотичних напружень формула
для розрахункових напружень набуває
вигляду:
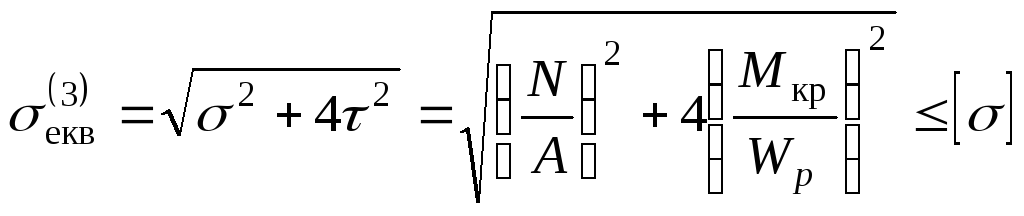. (12.41)
За четвертою теорією міцності ця формула має вигляд:
. (12.41)
Наведені
вище формули зручно використовувати
при вирішенні задачі перевірки напружень,
коли відомі значення внутрішніх силових
факторів
і
.
Розв’язуючи
задачу проектувального розрахунку,
коли розміри поперечного перерізу
невідомі, доводиться або заздалегідь
задаватися значеннями розмірів перерізу
при відомій його формі, або робити так,
як роблять при позацентровому розтяганні
або стисканні: нехтують впливом одного
з внутрішніх силових факторів, наприклад,
поздовжньої сили. Потім обчислюють
розміри поперечного перерізу, беруть
трохи завищені результати, а потім за
формулами (12.40), (12.41) виконують перевірку
напружень.
Ще складнішою є задача визначення величини допустимого навантаження, тому що на відміну від згинання з крученням при цьому виді деформації внутрішні силові фактори викликаються різними зовнішніми силами.
Таким чином, ми розглянули розрахунок елементів конструкцій і деталей машин, що зазнають складного опору різних видів, які належать двом групам: першій групі, коли в небезпечних точках поперечного перерізу виникає лінійний напружений стан і застосовується принцип прямого додавання напружень, викликаних різними силовими факторами (просторове і косе згинання, згинання з розтяганням і стисканням, позацентрове розтягання і стискання), і другий, коли в небезпечних точках перерізу виникає складний напружений стан, і для оцінки міцності необхідно застосовувати теорії міцності (згинання з крученням, кручення з розтяганням). В обох випадках складний вид деформації розкладається на ряд простих, в обох випадках будуються епюри розподілу внутрішніх силових факторів і знаходиться небезпечний переріз, визначаються небезпечні точки і напруження в цих точках від кожного з внутрішніх силових факторів окремо. І тільки на останньому етапі одержання розрахункових напружень методики розрахунку відрізняються способом оцінки міцності.
Крім розглянутих вище видів складного опору існує загальний випадок спільної дії згинання, розтягання і кручення, коли в поперечних перерізах елемента конструкції виникають усі шість внутрішніх силових факторів. Небезпечних точок у цьому випадку може бути декілька (Рис.12.32).
На рис.12.32,а наведений загальний випадок згинання, розтягання і кручення стержня прямокутного поперечного перерізу. Небезпечних точок тут дві: точки А і точка С. У точці А виникає лінійний напружений стан (Рис.12.32,б). Умова міцності набуває вигляду (12.6).
У точці С виникає плоский напружений стан (Рис.12.32,в). Максимальні дотичні напруження діють у точці С і можуть бути знайдені за допомогою формули (6.44), нормальні напруження в точці С можна визначити за допомогою формули (12.2).
Рис.12.32
Оцінку міцності в точці С можна виконати з застосуванням теорії найбільших дотичних напружень і енергетичної теорії, підставляючи знайдені в точці С нормальні і дотичні напруження безпосередньо у формули (12.41) або (12.42).