12.8. Згинання з крученням

Різні деталі машин, такі як розподільні вали, осі моторних вагонів електропоїздів і трамваїв, колінчаті вали зазнають одночасно дії згинання і кручення. При цьому тиск зубів на шестірні, натяг ременів, власна вага вала і шківів викликають у поперечних перерізах вала наступні внутрішні силові фактори: згинальні моменти і, крутний момент, поперечні сили. Впливом поперечних сил при згинанні з крученням, зазвичай, нехтують. Таким чином, у будь-якому поперечному перерізі виникають нормальні напруження від згинання у двох площинах і дотичні напруження від кручення.

Перш, ніж приступати до безпосереднього розрахунку валів на згинання з крученням, необхідно знайти небезпечний переріз і встановити вид напруженого стану, що виникає в деталі.

Розглянемо ламаний стержень круглого поперечного перерізу, затиснений на одному кінці і вільний на іншому (Рис.12.26,а).

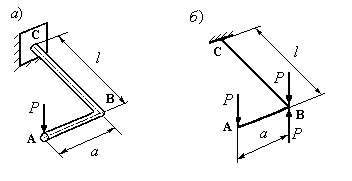
Рис.12.26

Розрахункова схема ламаного стержня наведена на рис.12.26,б.

Щоб знайти небезпечний переріз, розкладемо складний вид опору, яким є згинання з крученням, на два простих: плоске поперечне згинання і кручення. Для цього прикладемо в точці В дві рівні за величиною і протилежно спрямовані сили . Дві з цих сил створять пари сил з моментом. Таким чином, елемент ламаного стержня АВ зазнає плоского поперечного згинання, а елемент ВС зазнає згинання з крученням. Побудуємо епюри згинальних та крутних моментів для елемента стержня ВС (Рис.12.27,а).

Навантажимо елемент ВР тільки силою (Рис.12.27,б) і побудуємо епюру згинальних моментів від цієї сили(Рис.12.27,в).

Далі навантажимо елемент ВС тільки зовнішнім моментом (Рис.12.27,г), обчислимо крутний моменті побудуємо епюру крутних моментів (Рис.12.27,д).

Рис.12.27

Аналізуючи вид епюр, наведених на рис.12.27,в і 12.27,д, дістаємо висновку, що найбільш небезпечним є переріз С, тому що в цьому перерізі виникають найбільший згинальний момент і найбільший крутний момент.

Знайдемо тепер небезпечні точки в перерізі С (Рис.12.28,а). Для цього обчислимо в цьому перерізі максимальні нормальні напруження від згинання і найбільші дотичні напруження від крученняі побудуємо епюри розподілу нормальних (Рис.12.28,б) і дотичних напружень (Рис.12.28,в).

Небезпечними точками в перерізі С є точки D і К. При згинанні нормальні напруження визначаються за формулою:

.

Рис.12.28

Максимальні нормальні напруження виникають у найбільш віддалених точках поперечного перерізу. Такими точками є точки D і К. Напруження в цих точках знайдемо, скорставшись формулою:

(12.37)

Дотичні напруження від кручення визначаються з формулою:

.

Найбільші дотичні напруження виникають також у найбільш віддалених точках поперечного перерізу D і К. Для визначення максимальних дотичних напружень скористаємося формулою:

. (12.38)

Таким чином, при згинанні з крученням у поперечних перерізах в одній точці, найбільш віддаленої від центра ваги перерізу одночасно виникають максимальне нормальне і максимальне дотичне напруження. На рис.12.28,г показано, як діють ці напруження в точці D, на рис.12.28,д – те ж саме для точки К.

Напружений стан наведений на рисунках 12.28,в і 12.28,д, є складним. Принцип простого додавання напружень у цьому випадку не може бути застосований. Тому згинання з крученням і відноситься до другої групи видів складного опору. Для оцінки міцності у випадку виникнення складного напруженого стану застосовуються теорії міцності.

У даному випадку при згинанні з крученням у небезпечному поперечному перерізі С виникає плоский напружений стан. Застосуємо для оцінки міцності третю теорію міцності – теорію найбільших дотичних напружень. Розрахункові або еквівалентні напруження обчислимо за формулою:

.

Підставимо в наведену формулу максимальні нормальне і дотичне напруження (12.37), 12.38). Одержимо:

. (12.39)

При виводі формули (12.39) приймалося для круглого перерізу . Цю умову після нескладних перетворень можна одержати з умови інваріантності суми моментів інерції відносно двох взаємно перпендикулярних осей.

Буквою у формулі (12.39) позначений так званий зведений момент, який відповідно до третьої теорії міцності має вигляд:

. (12.40)

Відповідно до четвертої (енергетичної) теорією міцності зведений момент записується таким чином:

. (12.40)

Слід зазначити, що додавання моментів під коренем при обчисленні зведеного моменту не має ніякого фізичного змісту. Це все є лише результатом застосування тієї або іншої теорії міцності.

Розглянемо кілька прикладів розрахунку елементів конструкцій, які зазнають згинання з крученням.

Приклад 12.10. Порожнистий сталевий вал, у якого внутрішній діаметр складає 0,6 від зовнішнього, у небезпечному перерізі зазнає дії згинального моментукНм і крутного моментукНм. Визначити зовнішній і внутрішній діаметри вала при допустимому напруженніМПа. Використати теорію найбільших дотичних напружень.

Розв’язок:

1. За формулою (12.39) знайдемо зведений момент за третьою теорією міцності:

кНм.

2. З умови міцності (12.38) визначаємо необхідний момент опору перерізу:

см³.

3. Позначимо відношення внутрішнього діаметра до зовнішнього літерою і складемо вираз для осьового моменту опору поперечного перерізу вала:

.

Звідки знаходимо зовнішній діаметр перерізу

сммм.

4. Визначаємо внутрішній діаметр вала мм.

Приклад 12.11. Визначити найбільше розрахункове напруження в сталевому стержні АВ круглого поперечного перерізу діаметром мм, навантаженому двома однаковими вантажамикН, прикладеними, як показано на рис.12.29,а. Чому дорівнюватиме найбільше розрахункове напруження в стержні, якщо один з вантажів буде знятий? Використати четверту теорію міцності.

Рис.12.29

Розв’язок:

1. Знайдемо розрахункове напруження в стержні АВ для випадку, коли обидва вантажі діють на стержень. Для цього складемо розрахункову схему. Вантажі однакові і симетрично прикладені, діють в одному напрямку. Отже, стержень АВ зазнає деформацію плоского поперечного згинання. Розрахункова схема стержня наведена на рис.12.29,б. Епюра згинальних моментів наведена на рис.12.29,в, з якої видно, що небезпечним перерізом є переріз В. Максимальне напруження в цьому перерізі знайдемо, скориставшись формулою:

МПа.

Це напруження і буде розрахунковим.

Рис.12.30

2. Знімемо лівий вантаж (Рис.12.30,а). У цьому випадку стержень АВ буде згинатися силою кН і одночасно скручуватися моментомкНм. Розрахункова схема наведена на рис.12.30,б.

Розкладемо складний вид деформації на два простих. Спочатку навантажимо стержень АВ силою (Рис.12.30,в) і побудуємо епюру згинальних моментів (Рис.12.30,г). Потім навантажимо стержень АВ зовнішнім моментомі побудуємо епюру крутних моментів (Рис.12.30,е).

3. Аналізуючи епюри згинальних і крутних моментів, встановлюємо небезпечний переріз. Таким перерізом є переріз В: кНм;кНм.

4. Визначаємо зведений момент, використовуючи четверту теорію міцності:

кНм

і визначаємо розрахункове напруження

МПа.

Приклад 12.12. З умови міцності за теорією найбільших дотичних напружень визначити найбільшу допустиму величину вантажу , яку можна підняти за допомогою ворота (Рис.12.31,а). Вал ворота круглого поперечного перерізу діаметроммм. Допустиме напруження для матеріалуМПа.

Рис.12.31

Розв’язок:

1. Складемо розрахункову схему (Рис.12.31,б). З розрахункової схеми випливає, що вал зазнає деформації згинання від сили і кручення моментом. У зв'язку з цим розкладаємо складний вид опору на два простих – плоске поперечне згинання і кручення.

2. Зображуємо вал як балку (Рис.12.31,в), навантажуємо її силою посередині прольоту і будуємо епюру згинальних моментів (Рис.12.31,г). Максимальний згинальний моментвиникає в перерізі В.

3. Зображуємо вал і навантажуємо його тільки зовнішніми моментами (Рис.12.31,д) і будуємо епюру крутних моментів (Рис.12.31,е).

Крутний момент , має сталу величину і діє тільки на ділянці вала АВ.

4. Визначаємо небезпечний переріз. З епюр згинальних і крутних моментів івипливає, що небезпечним перерізом є переріз В:;.

5. Обчислюємо зведений момент для небезпечного перерізу, використовуючи третю теорію міцності:

.

6. З умови міцності за третьою теорією знаходимо максимальну допустиму величину вантажу :

, звідки кН.