
- •Тема 2 внутренние силовые факторы изгиба
- •2.1.Плоский поперечный изгиб. Поперечная сила и изгибающий момент
- •2.2. Дифференциальные зависимости при изгибе
- •2.3. Следствия из дифференциальных зависимостей
- •2.4. Построение эпюр поперечных сил и изгибающих моментов по “характерным”сечениям
- •2.5 Тесты к теме №2 “Внутренние силовые факторы изгиба”
2.4. Построение эпюр поперечных сил и изгибающих моментов по “характерным”сечениям
Дифференциальные зависимости между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом и изложенные выше следствия из этих зависимостей позволяют не только контролировать правильность построения эпюр внутренних силовых факторов при изгибе, но и строить эпюры поперечных сил и изгибающих моментов по “характерным” сечениям. Этот метод существенно отличается от аналитического метода, так как в результате его применения нельзя получить уравнения распределения внутренних силовых факторов в пределах рассматриваемого участка изгибаемого элемента конструкции. С помощью этого метода можно получить лишь численные значения поперечной силы и изгибающего момента в том или ином сечении. Однако такой подход в сочетании с использованием следствий из дифференциальных зависимостей между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом позволяет быстро и качественно строить эпюры различной сложности. “Характерными” будем называть поперечные сечения, расположенные бесконечно близко к границам участка изгибаемого элемента конструкции.
Рассмотрим применения этого метода на примере.
Пример
2.8. Построить
эпюры поперечных сил
![]() и изгибающих моментов
и изгибающих моментов![]() для изображенной на рис.2.16,а балки по
методу“характерных”
сечений.
для изображенной на рис.2.16,а балки по
методу“характерных”
сечений.
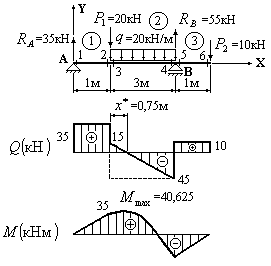
Рис.2.16
Решение:
1. Определяем опорные реакции. Для этого составим два уравнения равновесия:
![]() ;
(а)
;
(а)
![]() .
(б)
.
(б)
Из
уравнения (а) находим величину реакции
![]() :
:
![]() кН.
кН.
Из
уравнения (б) находим величину реакции
![]() :
:
![]() кН.
кН.
Выполняем
проверку. Для этого составим уравнение
проекций всех сил, действующих на балку,
на вертикальную ось
![]() :
:
![]() .
.
2. Разбиваем балку на участки и проставляем “характерные” сечения 1 6 на границах участков.
3. Определяем величины для поперечной силы в каждом из “характерных” сечений:
![]() кН;
кН;
![]() кН;
кН;![]() кН;
кН;
![]() кН;
кН;
![]() кН;
кН;![]() кН.
кН.
Откладываем от базисной линии найденные значения для поперечной силы в каждом из “характерных” сечений и соединяем полученные точки, руководствуясь следствиями из дифференциальных зависимостей между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом.
На участке №1 распределенная нагрузка отсутствует. Следовательно, на основании первого следствия из дифференциальных зависимостей поперечная сила будет постоянной. Соединяем точки, соответствующие значениям поперечной силы, найденным в сечениях №1 и №2, горизонтальной прямой. На втором участке действует распределенная нагрузка постоянной интенсивности. Следовательно, на основании следствия №2 из дифференциальных зависимостей поперечная сила должна меняться по линейному закону. Поэтому соединяем точки соответствующие значениям поперечной силы, найденным в сечениях №3 и №4 наклонной прямой. На участке №3 распределенная нагрузка так же, как и на участке №1, отсутствует. Следовательно, на основании первого следствия из дифференциальных зависимостей поперечная сила будет постоянной. Соединяем точки, соответствующие значениям поперечной силы, найденным в сечениях №5 и №6 горизонтальной прямой.
При
построении эпюры поперечных сил следует
обращать внимание на возможные скачки
в тех сечениях, в которых приложены
сосредоточенные силы. Так, в сечениях
№2 и №3 значения для поперечной силы
отличаются на величину силы
![]() .
В сечениях №4 и №5 значения для поперечной
силы отличаются на величину реакции
.
В сечениях №4 и №5 значения для поперечной
силы отличаются на величину реакции![]() .
В сечении №6 также наблюдается скачок
на величину силы
.
В сечении №6 также наблюдается скачок
на величину силы![]() в направлении ее действия при построении
эпюры слева направо.
в направлении ее действия при построении
эпюры слева направо.
4. Находим значения для изгибающих моментов в “характерных” сечениях:
![]() ;
;
![]() кНм;
кНм;![]() кНм;
кНм;
![]() кНм;
кНм;
![]() кНм;
кНм;![]() .
.
Откладываем от базисной линии найденные значения для изгибающих моментов в “характерных” сечениях и соединяем полученные точки, руководствуясь следствиями из дифференциальных зависимостей между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом.
На участке №1 распределенная нагрузка отсутствует. Следовательно, на основании первого следствия из дифференциальных зависимостей изгибающий момент будет меняться по линейному закону. Соединяем точки, соответствующие значениям изгибающих моментов, найденным в сечениях №1 и №2, наклонной прямой. На втором участке действует распределенная нагрузка постоянной интенсивности. Следовательно, на основании следствия №2 из дифференциальных зависимостей изгибающий момент должен меняться по закону квадратной параболы. При этом на основании следствия №4 выпуклость на эпюре изгибающих моментов должна быть обращена навстречу распределенной нагрузке, т.е. вверх. Соединяем точки, соответствующие значениям изгибающих моментов, найденным в сечениях №3 и №4 параболой, обращенной выпуклостью вверх. На участке №3 распределенная нагрузка так же, как и на участке №1, отсутствует. Следовательно, на основании первого следствия из дифференциальных зависимостей изгибающий момент будет меняться по линейному закону. Поэтому соединяем точки, соответствующие значениям изгибающих моментов, найденных в сечениях №5 и №6 наклонной прямой. Скачков на эпюре изгибающих моментов не наблюдается, так как отсутствуют сосредоточенные моменты, приложенные к балке. Следует обратить внимание, что в сечениях, в которых имеются скачки на эпюре поперечных сил, на эпюре изгибающих моментов должны быть изломы.
Найдем
величину максимального изгибающего
момента
![]() .
На втором участке балки поперечная сила
меняет знак, пересекая базисную линию.
Сечение, в котором поперечная сила равна
нулю, также считается“характерным”.
В этом сечении изгибающий момент
достигает экстремальной величины на
рассматриваемом участке. Для рассматриваемой
балки изгибающий момент будет максимальным
на основании дифференциальной зависимости
(2.15), так как интенсивность распределенной
нагрузки
.
На втором участке балки поперечная сила
меняет знак, пересекая базисную линию.
Сечение, в котором поперечная сила равна
нулю, также считается“характерным”.
В этом сечении изгибающий момент
достигает экстремальной величины на
рассматриваемом участке. Для рассматриваемой
балки изгибающий момент будет максимальным
на основании дифференциальной зависимости
(2.15), так как интенсивность распределенной
нагрузки
![]() .
.
Для определения
максимального изгибающего момента
сначала определим координату сечения,
в котором момент максимален. Для этого
на эпюре поперечных сил сформируем два
треугольника (контур одного из
треугольников показан пунктиром). Один
из рассматриваемых треугольников имеет
неизвестный катет длиной
![]() ,
который и следует определить. Выделенные
треугольники подобны по трем углам.
Составим пропорцию:
,
который и следует определить. Выделенные
треугольники подобны по трем углам.
Составим пропорцию:![]() ,
решая которую относительно
,
решая которую относительно![]() ,
получим
,
получим![]() м.
м.
Максимальный изгибающий момент можно определить двумя способами:
1.
Помещая начало координат в точке А балки
на левом ее конце, вычислим координату
сечения, в котором изгибающий момент
достигает максимальной величины:
![]() м,
составляем выражение для изгибающего
момента в указанном сечении и подставляем
в это выражение координату
м,
составляем выражение для изгибающего
момента в указанном сечении и подставляем
в это выражение координату![]() м.
Получим:
м.
Получим:
![]() кНм.
кНм.
2.
Используя следствие №5 из дифференциальных
зависимостей между интенсивностью
распределенной нагрузки, поперечной
силой и изгибающим моментом, максимальный
изгибающий момент найдем, прибавив к
значению изгибающего момента в сечении
№3 площадь эпюры поперечной силы
![]() на участке длиной
на участке длиной![]() м:
м:
![]() кНм.
кНм.
Последний способ определения изгибающих моментов в некоторых случаях может оказаться предпочтительнее, так как существенно экономит время.
Пример
2.8. Используя
метод “характерных”
сечений, построить эпюры распределения
поперечных[
сил
![]() ,
изгибающих моментов
,
изгибающих моментов![]() и продольных сил
и продольных сил![]() для
статически определимой рамы, изображенной
на рис. 2.17.
для
статически определимой рамы, изображенной
на рис. 2.17.
Решение:
1.Определяем опорные реакции:
![]() ;
(а)
;
(а)
![]() ;
(б)
;
(б)
![]() .
(в)
.
(в)
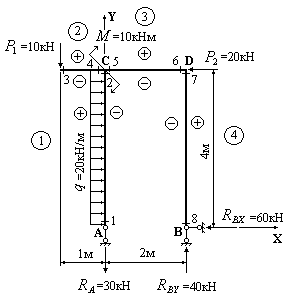
Рис.2.17
Из
уравнения (а) находим реакцию
![]() :
:
![]() кН.
кН.
Из
уравнения (б) находим реакцию
![]() :
:
![]() кН.
кН.
Из
уравнения (в) находим реакцию
![]() :
:
![]() кН.
кН.
Реакции получились положительными. Следовательно, их направления выбраны верно.
Выполним
проверку. Для этого составим сумму
проекций всех сил на ось
![]() .
Эта сумма должна тождественно равняться
нулю:
.
Эта сумма должна тождественно равняться
нулю:
![]() .
.
2. Расставляем реакции, разбиваем раму на участки, выбираем точку наблюдения, расставляем знаки на каждом участке для поперечных сил и изгибающих моментов и расставляем номера “характерных” сечений таким образом, чтобы нумерация сечений производилась слева направо. При этом знак «+» должен находиться над участком, знак «» – под участком.
3. Определяем значения поперечных сил в “характерных” сечениях рамы:
![]() ;
;
![]() кН;
кН;
![]() кН;
кН;![]() кН;
кН;
![]() кН;
кН;
![]() кН;
кН;![]() кН;
кН;![]() кН.
кН.
Строим эпюру поперечных сил (Рис.2.18):

Рис.2.18
4. Определяем значения для изгибающих моментов в “характерных”сечениях рамы:
![]() ;
;![]() кНм;
кНм;![]() ;
;![]() кНм;
кНм;
![]() кНм;
кНм;![]() кНм;
кНм;
![]() кНм;
кНм;![]() .
.
Строим эпюру изгибающего момента (Рис.2.19):

Рис.3.19
5. Выполняем статическую проверку. Статическая проверка состоит а кинематической проверке расновесия узлов рамы. Вырежем сечениями №2, №4 и №5 первый узел С и изобразим его на рис. 2.20,а. Приложим к узлу моменты, характеризующие влияние отброшенной части рамы на узел. Эти моменты численно равны значениям изгибающих моментов соответственно в сечениях №2, №4 и №5. Направление действия этих моментов определяется правилом знаков для изгибающего момента. Значения моментов на рис 2.20 приведены в кНм.

Рис.2.20
Рассматривая равновесие узла С, выделенного из рамы сечениями №2, №4 и №5, составляем уравнение для суммы моментов относительно центра узла. В данном случае следует учитывать, что на узел С действует внешний заданный момент М.
![]() . (а)
. (а)
Как видно из уравнения (а) узел С находится в равновесии. Выполним проверку узла D, выделенного из рамы сечениями №6 и №7 (Рис.2.20,б). Составим сумму моментов, действующих на узел D:
![]() .
(б)
.
(б)
Как видно из уравнения (б) узел Dтакже находится в равновесии.
6. Определяем
величину продольной силы в стержнях
рамы. Для этого вырежем сечениями №2,
№4 и №5 узел Cи изобразим
его на рис. 2.21,а. Приложим к узлуC
продольные усилия![]() и поперечные силы
и поперечные силы![]() ,
характеризующие влияние отброшенной
части рамы на узел. Эти усилия численно
равны значениям соответственно продольных
и поперечных сил в сечениях №2, №4 и №5.
Направление действия этих усилий
определяется правилом знаков для
продолных усилий и поперечных сил.
Значения поперечных сил на рис 2.21
приведены в кН.
,
характеризующие влияние отброшенной
части рамы на узел. Эти усилия численно
равны значениям соответственно продольных
и поперечных сил в сечениях №2, №4 и №5.
Направление действия этих усилий
определяется правилом знаков для
продолных усилий и поперечных сил.
Значения поперечных сил на рис 2.21
приведены в кН.
Составим суммы
проекций сил, приложенных к узлу
C, на оси![]() и
и![]() :
:
![]() (в)
(в)
![]() (г)
(г)

Рис.2.21
Рассматривая
уравнение (в), обнаруживаем, что в этом
уравнении две неизвестных продольных
силы
![]() и
и![]() .
Решить это уравнение относительно
усилий
.
Решить это уравнение относительно
усилий![]() и
и![]() невозможно. Найдем сначала усилие
невозможно. Найдем сначала усилие![]() ,
рассмотрев равновесие участка рамы,
ограниченного сечениями №3 и №4
(Рис.2.22).
,
рассмотрев равновесие участка рамы,
ограниченного сечениями №3 и №4
(Рис.2.22).

Рис.2.22
Составим для
изображенного на рис.2.22 стержня условие
равновесия приложенных к стержню сил,
на ось
![]() :
:
![]() ,
(д)
,
(д)
откуда
![]() .
.
Но усилие
![]() ,
так как в сечение №3 отсутствуют силы,
действующие вдоль участка стержня 3-4
(Рис.2.17). Следовательно,усилие
,
так как в сечение №3 отсутствуют силы,
действующие вдоль участка стержня 3-4
(Рис.2.17). Следовательно,усилие![]() .
Теперь можно определить остальные
продольные усилия, действующие в узле
C. Из уравнения (в) находим:
.
Теперь можно определить остальные
продольные усилия, действующие в узле
C. Из уравнения (в) находим:
![]() кН.
кН.
Из уравнения
(г) найдем усилие
![]() :
:
![]() кН.
кН.
Найдем продольные
усилия в сечениях №6 и №7. Для этого
составим уравнения равновесия сил,
приложенных к узлу Dна
горизонтальную и вертикальную оси
координат Х и Y (Рис.2.21,б). При
составлении этих уравнений не следует
забывать, что к узлуD приложена
сосредоточенная сила![]() .
.
![]() ;
(е)
;
(е)
![]() .
(ж)
.
(ж)
Из уравнения (е) находим продольную силу в сечении №6:
![]() кН.
кН.
Из уравнения (ж) находим продольную силу в сечении №7:
![]() кН.
кН.
Откладываем
найденные значения для продольной силы
и строим эпюру продольных усилий
![]() (Рис.2.23).
(Рис.2.23).

Рис.2.23
Приведенные примеры построения эпюр поперечных сил и изгибающих моментов для балок и эпюр поперечных сил, изгибающих моментов и продольных усилий для рам позволяют получить наглядное представление о преимуществах и недостатках метода “характерных”сечений. К числу преимуществ этого метода можно отнести простоту определения внутренних силовых факторов. К числу недостатков – отсутствие аналитических законов распределения внутренних силовых факторов по длине элементов конструкции. Однако, использования дифференциальных зависимостей между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом для анализа поведения распределения внутренних усилий и следствий из них в значительной мере компенсирует последний недостаток. Сделанный вывод позволяет рекомендовать метод построения эпюр распределения внутренних силовых факторов по“характерным’сечениям в учебную практику.
