
- •1. Границя послідовності
- •1.1. Числова послідовність
- •1.2. Обмежені й необмежені послідовності
- •1.3. Монотонні послідовності
- •1.4. Число е
- •2. Границя функції
- •Геометричний зміст границі функції у точці
- •Геометричний зміст границі функції у нескінченності
- •2.1. Властивості нескінченно малих функцій
- •2.2. Порівняння нескінченно малих функцій
- •2.3. Властивості еквівалентних нескінченно малих
- •2.4. Теореми про границі
- •3. Методичні рекомендації
- •4. Індивідуальні завдання Знайти границі
1.4. Число е
Розглянемо
послідовність {xn}
=
![]() .
.
Якщо послідовність {xn} монотонна й обмежена, то вона має кінцеву границю.
За формулою бінома Ньютона:
![]()
або, що те ж саме
![]()
Покажемо, що послідовність {xn} – зростаюча. Дійсно, запишемо вираз xn+1 і зрівняємо його з виразом xn:
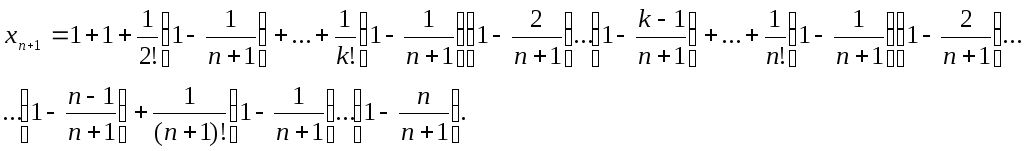
Кожен доданок у виразі xn+1 більший відповідного значення xn, і, крім того, в xn+1 додається ще один позитивний доданок. Таким чином, послідовність {xn} зростаюча.
Доведемо тепер, що при будь-якому n її члени не перевершують трьох:
xn < 3.
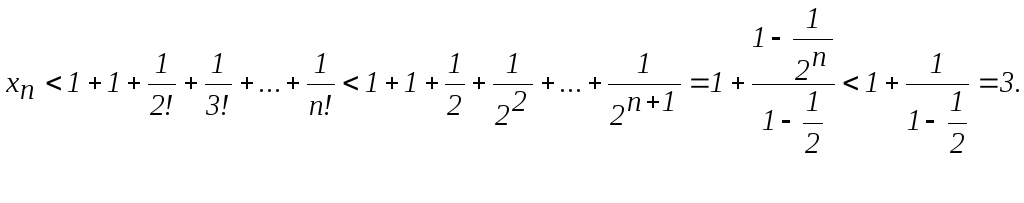
геометрична прогресія
Отже, послідовність
![]() – монотонно зростаюча та обмежена
зверху, тобто має кінцеву границю. Цю
границю прийнято позначати буквоюе.
– монотонно зростаюча та обмежена
зверху, тобто має кінцеву границю. Цю
границю прийнято позначати буквоюе.
![]() .
.
З нерівності
![]() треба, щобе
3. Відкидаючи в рівності для {xn}
всі члени, починаючи із четвертого,
маємо:
треба, щобе
3. Відкидаючи в рівності для {xn}
всі члени, починаючи із четвертого,
маємо:
![]() ,
,
переходячи до границі, одержуємо
![]() .
.
Таким чином, число е укладене між числами 2,5 й 3. Якщо взяти більшу кількість членів ряду, то можна одержати більш точну оцінку значення числа е.
Можна показати, що число е ірраціональне і його значення дорівнює 2,71828...
Аналогічно
можна показати, що
![]() ,
розширивши вимоги до х до будь-якого
дійсного числа:
,
розширивши вимоги до х до будь-якого
дійсного числа:
Припустимо:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Знайдемо
![]()
Число е є основою натурального логарифма.
![]()
Рис. 1.3
![]()
Вище наданий графік функції y = lnx.
2. Границя функції
Поняття границі функції є узагальненим поняттям границі послідовності, тому що границю послідовності можна розглядати як границю функції xn = f(n) цілочисельного аргументу n.
Визначення.
Число А називається
границею функції
![]() у точці
у точці![]() (або при
(або при![]() ),
якщо для будь-якого як завгодно малого
числа
),
якщо для будь-якого як завгодно малого
числа![]() можна знайти таке число
можна знайти таке число![]() ,
що для
,
що для![]() ,
які задовольняють нерівність
,
які задовольняють нерівність
![]()
виконується нерівність
![]() .
.
Якщо число А границя
функції в точці
![]() ,
то пишуть:
,
то пишуть:
![]() або
або
![]() при
при![]() .(2.2)
.(2.2)
Геометричний зміст границі функції у точці
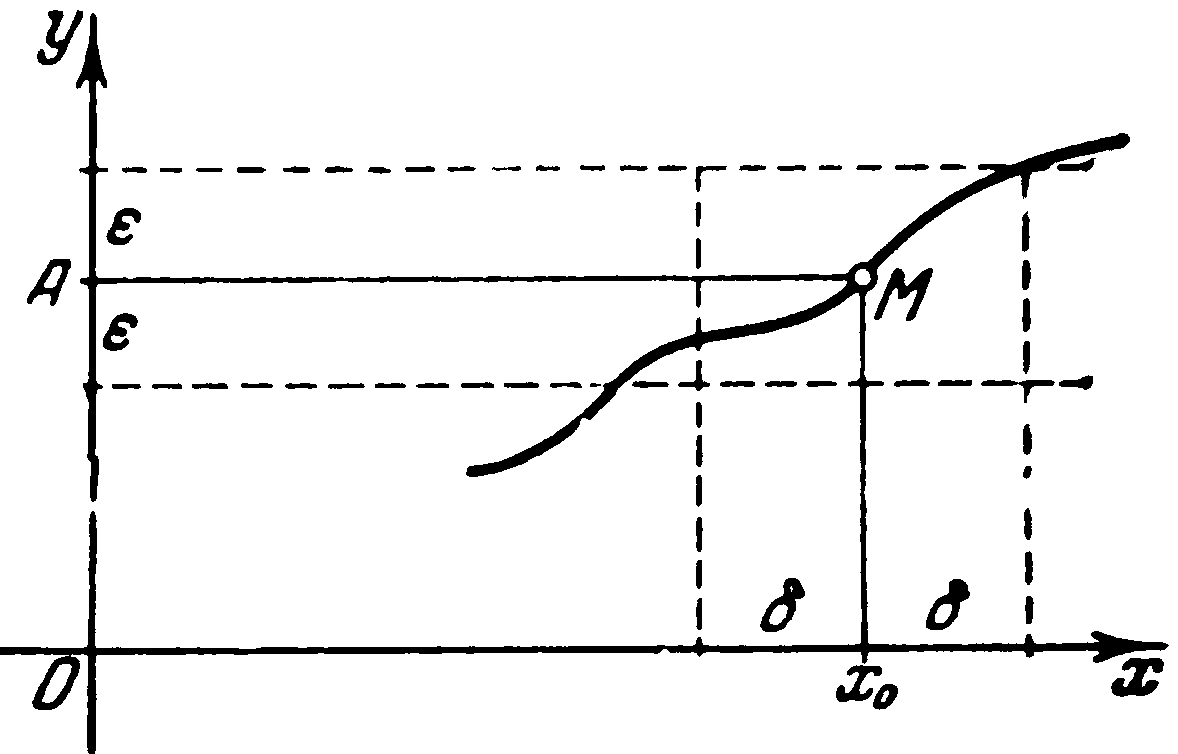
Рис. 2.1
ЗАУВАЖЕННЯ.
Визначення границі не вимагає існування
функції у самій точці
![]() ,
тому що розглянуті значення
,
тому що розглянуті значення![]() в деякій околиці точки
в деякій околиці точки![]() .
Інакше кажучи, розглядаючи
.
Інакше кажучи, розглядаючи
![]() ,ми
припускаємо, що
,ми
припускаємо, що
![]() ,
але не досягає значення
,
але не досягає значення![]() .
Тому наявність або відсутність границі
при
.
Тому наявність або відсутність границі
при![]() визначається поведінкою функції в
околиці точки
визначається поведінкою функції в
околиці точки![]() ,
але не пов’язане зі значенням функції
(або його відсутністю) у самій точці
,
але не пов’язане зі значенням функції
(або його відсутністю) у самій точці![]() .
.
Визначення.
Якщо f(x)
A1
при х
а тільки при x < a, то
![]() – називаєтьсяграницею
функції f(x) у точці х = а ліворуч,
а якщо f(x)
A2
при х
а тільки при x > a, то
– називаєтьсяграницею
функції f(x) у точці х = а ліворуч,
а якщо f(x)
A2
при х
а тільки при x > a, то
![]() називаєтьсяграницею
функції f(x) у точці х = а праворуч.
називаєтьсяграницею
функції f(x) у точці х = а праворуч.
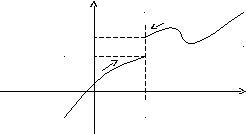 в
в
f(x)
А2
А1
0 a x
Рис. 2.2
Наведене вище визначення ставиться до випадку, коли функція f(x) не визначена в самій точці х = а, але визначена в деякій як завгодно малій околиці цієї точки.
Границі А1 й А2 називаються також однобічними границями функції f(x) у точці х = а. Також говорять, що А – кінцева границя функції f(x).
Визначення.
(у нескінченності)
Число А називають границею
функції
![]() при
при![]() ,
що прагне до
,
що прагне до![]() ,
якщо для
,
якщо для![]() ,
навіть як завгодно малого невід’ємного
числа
,
навіть як завгодно малого невід’ємного
числа![]() ,
знайдеться таке невід’ємне число
S=S(
,
знайдеться таке невід’ємне число
S=S(![]() ),
що для всіх таких
),
що для всіх таких![]() :
:![]() виконується нерівність
виконується нерівність![]() .
Позначають
.
Позначають
![]() . (2.3)
. (2.3)
