
- •Методичні вказівки та індивідуальні завдання
- •Відповідальний за випуск д.Г. Зеленцов, д-р техн. Наук
- •Основні питання програми дисципліни за темою «диференціальне числення функцій однієї змінної»
- •Орієнтовний перелік питань для підсумкового контролю знань
- •1. Визначення похідної. Диференціювання функцій
- •1.3. Таблиця похідних функцій:
- •2. Геометричне застосування похідної
- •3. Диференціювання функцій, заданих параметрично
- •5. Правило лопіталя
- •Список літератури
Орієнтовний перелік питань для підсумкового контролю знань
Похідна функції. Основні формули й правила диференціювання.
Механічна й геометрична інтерпретації похідної.
Теорема про зв’язок неперервності і диференційованості функції.
Похідна складної функції. Логарифмічна похідна.
Похідна оберненої функції. Похідна функції, що задана параметрично.
Диференціал функції. Геометричний зміст диференціала. Властивості диференціала.
Застосування диференціала до наближених обчислень.
Похідні та диференціали вищих порядків.
Правило Лопіталя щодо розкриття невизначеностей виду
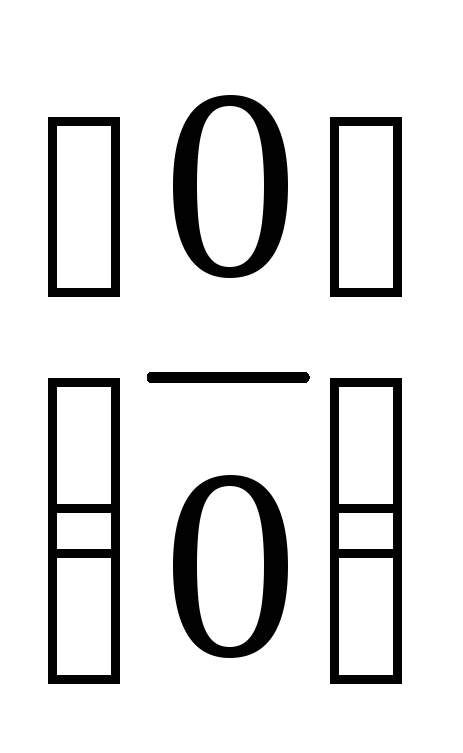 .
.Правило Лопіталя щодо розкриття невизначеностей виду
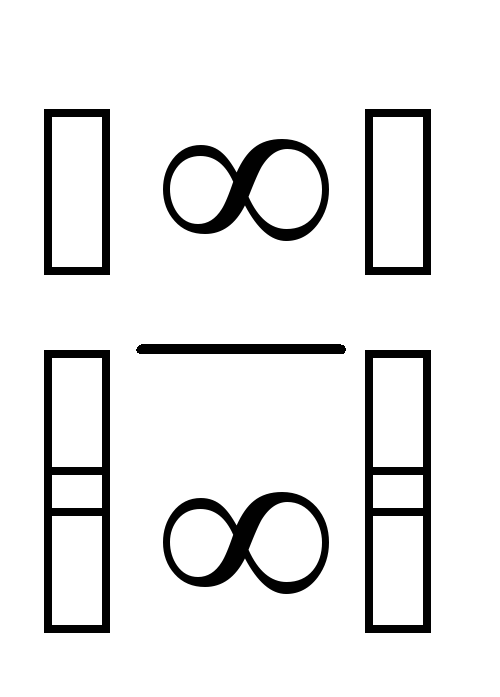 .
.Ознаки монотонності функції.
Екстремум функції. Необхідна й достатні умови існування екстремуму.
Умови опуклості та увігнутості кривої.
Точки перегину. Необхідна й достатня умови існування точок перегину.
Асимптоти графіка функції. Види асимптот.
1. Визначення похідної. Диференціювання функцій
1.1. Похідною
функції![]() називається границя відношення приросту
цієї функції до відповідного приросту
аргументу
називається границя відношення приросту
цієї функції до відповідного приросту
аргументу![]() ,
коли приріст аргументу прямує до нуля:
,
коли приріст аргументу прямує до нуля:
![]() .
.
Якщо ця границя
кінцева, то похідна існує, й функція
![]() називаєтьсядиференційованою в точці
називаєтьсядиференційованою в точці
![]() .
Похідна позначається також
.
Похідна позначається також![]() або
або![]() .
Операція відшукання похідної називаєтьсядиференціюванням функції.
.
Операція відшукання похідної називаєтьсядиференціюванням функції.
1.2.
Правила диференціювання функцій.
Нехай ![]() – стала,
– стала, ![]() ,
,
![]() – функції, що мають
похідні.
– функції, що мають
похідні.
|
1.
|
|
|
|
2.
|
|
|
|
3.
|
|
|
|
4.
|
|
|
5. Правило
диференціювання складної функції.Якщо функція![]() диференційована по
диференційована по![]() ,
а функція
,
а функція![]() – по
– по![]() ,
то складна функція
,
то складна функція![]() має похідну
має похідну![]() чи
чи![]() .
.
1.3. Таблиця похідних функцій:
|
Похідні основних елементарних функцій |
Похідні складних елементарних функцій,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.4. Похідні вищих
порядків.
Похідною
другого порядку (другою похідною)
від функції
![]() називається похідна від її похідної,
тобто
називається похідна від її похідної,
тобто
![]() .
.
Другу похідну
також позначають
![]() або
або![]() .
Похідна від похідної другого порядку
називаєтьсяпохідною
третього порядку
і так далі. Похідну
.
Похідна від похідної другого порядку
називаєтьсяпохідною
третього порядку
і так далі. Похідну ![]() -го
порядку позначають
-го
порядку позначають
![]() або
або![]() .
.
1.5. Приклади. Використовуючи правила диференціювання й таблицю похідних, знайдемо похідні наступних функцій:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
|
7)
|
|
|
Розв’язання
1) Перепишемо задану
функцію, надавши доданки у вигляді
степеня:
![]() .
Тоді застосувавши формулу 2
п. 1.2
правил диференціювання, а також формулу 1а
п. 1.3:
.
Тоді застосувавши формулу 2
п. 1.2
правил диференціювання, а також формулу 1а
п. 1.3:
![]() .
.
2) Записуємо задану
функцію у вигляді степеня:
![]() та обчислюємо похідну,
застосувавши
формулу 1а п. 1.3:
та обчислюємо похідну,
застосувавши
формулу 1а п. 1.3:
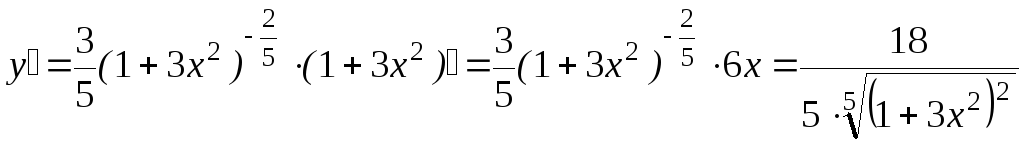 .
.
3) Застосувавши формулу 3 п. 1.2 правил диференціювання, а також формулу 1 та формулу 14 п 1.3, знаходимо:
![]() .
.
4) Диференціюючи
функцію
![]() як складну, знаходимо похідну:
як складну, знаходимо похідну:
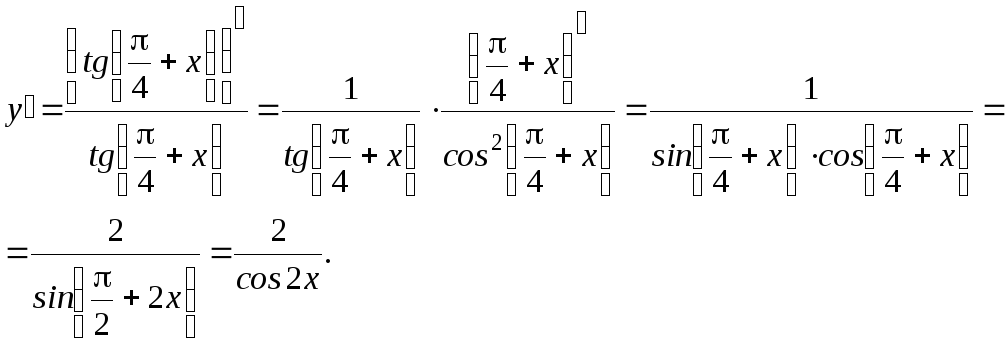
5) Відповідно до формули 4 п. 1.2 одержуємо:
![]() .
.
6) За аналогією із прикладом 3 знаходимо:
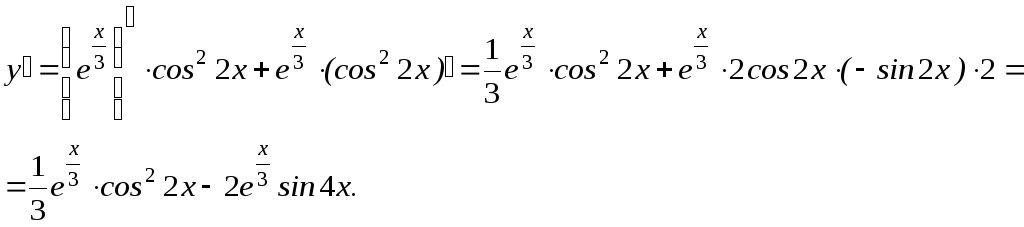
7) Так як дана функція – показникова, то відповідно до формули 5а п.1.3:
![]()
1.6. Степенево-показникова
функція.
Виведемо формулу для похідної
степенево-показникової функції
![]() ,
враховуючи, що
,
враховуючи, що![]() та
та![]() диференційовані функції та
диференційовані функції та![]() .
.
Логарифмуючи
рівність
![]() і диференціюючи обидві частини отриманої
рівності
і диференціюючи обидві частини отриманої
рівності![]() ,
знаходимо:
,
знаходимо:![]() .
Отже,
.
Отже,![]() . Таким чином, одержуємо
. Таким чином, одержуємо![]() .
.
Наприклад, знайти
похідну функції
![]() ,
де
,
де![]() .
.
Прологарифмуємо
задану функцію:
![]() .
Використовуючи основні властивості
логарифмів (
.
Використовуючи основні властивості
логарифмів (![]() ,
,![]() ,
,![]() ),
отримаємо:
),
отримаємо:![]() .
.
Продиференціюємо
отриману неявну функцію:
![]() .
Відповідно до формули 9а п.1.3 (для лівої
частини) та до формули 3 п.1.2 (для правої
частини), отримуємо:
.
Відповідно до формули 9а п.1.3 (для лівої
частини) та до формули 3 п.1.2 (для правої
частини), отримуємо:![]() ;
;![]() ;
;![]() .
Далі:
.
Далі:![]() .
Підставивши задану спочатку функцію в
останній вираз, отримаємо:
.
Підставивши задану спочатку функцію в
останній вираз, отримаємо:![]() .
.
Завдання 1. Знайти перші похідні функцій. У завданнях а) і б) додатково знайти другі похідні.
|
|
а) у =
б) у =
в) у = ( х + 2)
г) у =
д)
у = |
|
|
а) у =
б) у =
в) у =
г) у = ln
sin (2x
+ 5); и) у =
д)
у =
|
|
|
а) у =
б) у =
в) у = (ln x +1)2 cos 2x ; з) у = sin2 2x+ cos x ;
г) у = arcsin д)
у = 5 tg
x +
3 |
|
|
а) у =
б) у =
в) у =arcsin(3x2
+ 2); з) у = ( 2х + 5)
г) у =
д) у =
|
|
|
а) у =
б) у =
в) у = arctg
г) у = х
arccos
д) у =
|
|
|
а) у =
б) у =
в) у =
г) у =
д) у = ( х + х 2
) х ; к) у =
|
|
|
а) у =
б) у =
в) у =
г) у = arctg(ln x) +ln(sinx); и) у = ln 5( x 2 – 1);
д) у = 2
cos(4x+x2); к)
у =
|
|
|
а) у =
б) у = в) у = 3х arcsin 2x; з) у = (х2 + 2х + 2) е -х;
г) у =
д) у = 3
ctg
x
+ 8
|
|
|
a)
у =
б) у =
в) у =
г) у = ln
3 sin
(3x + 3); и) у =
д) у =
|
|
|
a)
у =
б) у =
в) у =
г) у = ln (2x3 +3x2 ); и) у = arctg 2 e x ;
д) у =
|
|
|
a)
у =
б) у = (5х + х
3 )
ln x
2; ж) у =
в) у =
г) у = arccos
д) у = 0,7
arctg
х; к) у =
|
|
|
а) у = 3х
5 –
б) у =
в) у = (х + 1)2
cos5x; з)
у = 23х + 7х 7
+
г) у = arctg(е2x
+ 3); и) у =
д) у =
|
|
|
a)
у =
б) у =
в) у =
г) у = х
arccos x
–
д) у =
|
|
|
а) у =
б) у =
в) у = (3 – sin 2 x) 3 ; з) у = х 2 ln(x 2 + 1);
г) у =
д)
у =
|
|
|
a)
у =
б) у =
в) у = (5 + х
3 ) 2
е –х; з) у =
г) у =
д)
у =
|
|
|
a)
у =
б) у =
в) у =
г) у = 2tg
3(x
3 + 2) ; и) у = arctg
2
д) у = 2 sin
3x; к) у
=
|
|
|
a)
у =
б) у = ln
ctg 3
x; ж) у =
в) у =
г) у = arctg(tg
2 x
+ 2 ); и) у =
д) у =
|
|
|
а) у
= 3x5
–
б) y = arcsin (3x3 + 4); ж) y = ln cos(5x 3 + 4); в) y = ( x+ 8) arctg 4x3 ; з) y = ( ctg 3x + 1 )5;
г) y =
д) y
= 4x
( 1 – 3ln x); к)
y = (cos
x )
|
|
|
a)
у = x7
–
б) у =
в) у =
г) у =
д) у = ln
2 sin3x; к)
у =
|
|
|
a)
у =
б) у =
в) у =
г) у =
arctg(7sin3x); и)
у =
д) у =
|
|
|
a)
у =
б) у =
в) у =
г) у =
д)
у =
|
|
|
а) у
=
б) у =
в) у = х
2
г) у =arctg
д) у =
|
|
|
a) y
=
б) у =
в) у =
г) у =
д) у =
|
|
|
a)
у =
б) у = tg
x +
в) у = х
3 ( х –
5 cos x
)2 з) у = arccos
г) у =
д)
у = 5 |
|
|
a)
у =
б) у =
в) у = arctg( x 2+e3x); з) у = (2х3 + 5)4 х 3; г) у = ln tg (5x+1); и) у = sin 5x+cos 3x 3; д)
у = 3ln3x; к)
у =
|
|
|
a) y
=
б) у = arctg
в) у =
г) у = х2
ctg2x
; и) у =
д) у = cos25x + 7x; к) у = (cos x )sin x.
|
|
|
а) y
=
б) у = tg
( x 2
+3); ж) у =
в) у =
г) у = ln
tg д)
у = х 2
arcsin (9x
+ 2) ; к) у =
|
|
|
а) у =
б) у =
в) у = (х + 5) 7 sin3x; з) у = (х+1) arccos (x 2 +1);
г) у =
д) у = 52ctg x ; к) у = (tg x)х.
|
|
|
а) у =
б) у =
в) у =
г) у = arctg 2 x + 6x2; и) у = ( х 3 + х 2 ) е –х; д)
у =
|
|
|
а) у =
б) у = 3х sin 5x + 8; ж) у =х (cos ln x + sin lnx);
в) у = (3 + sin
x) 2
x; з) у =
г) у =
д)
у =
|

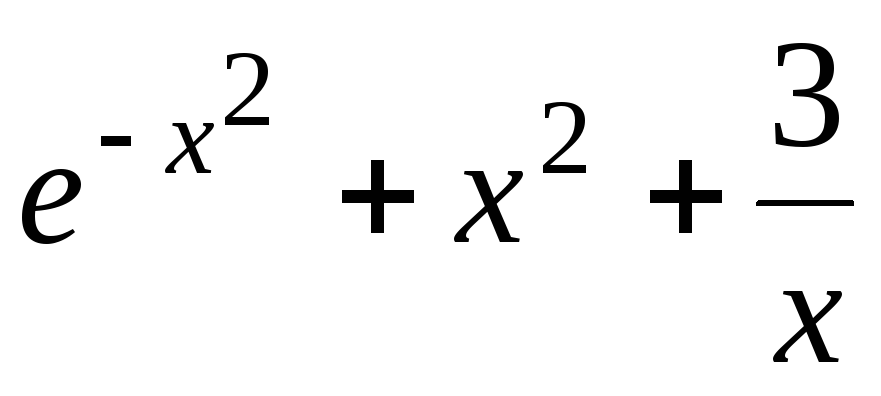 ;
;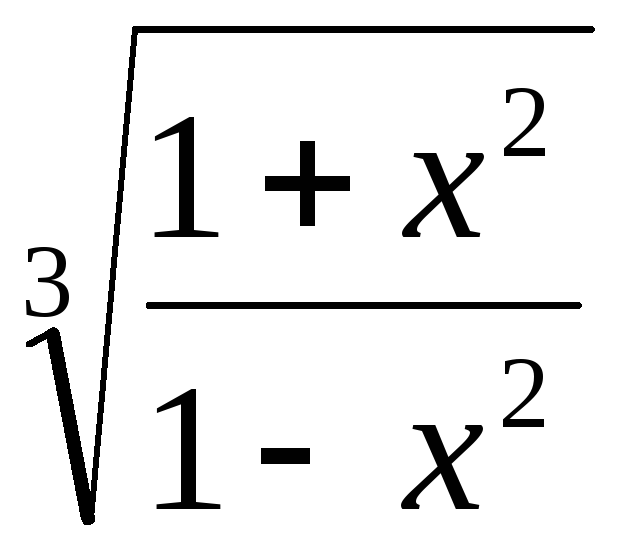 ; ж)
у =ln
; ж)
у =ln
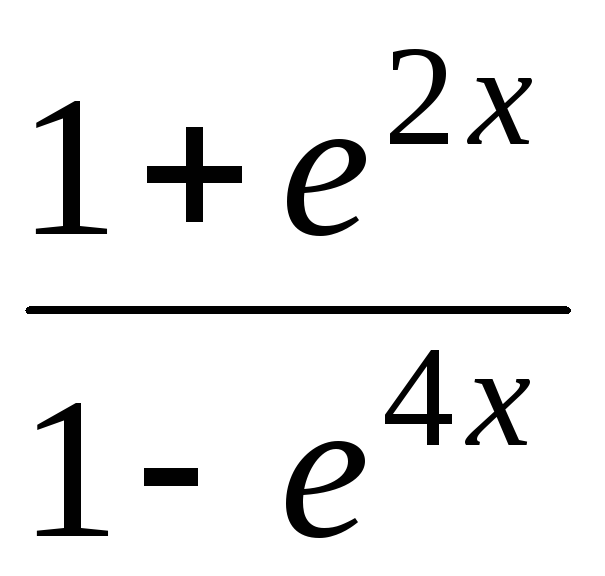 ;
;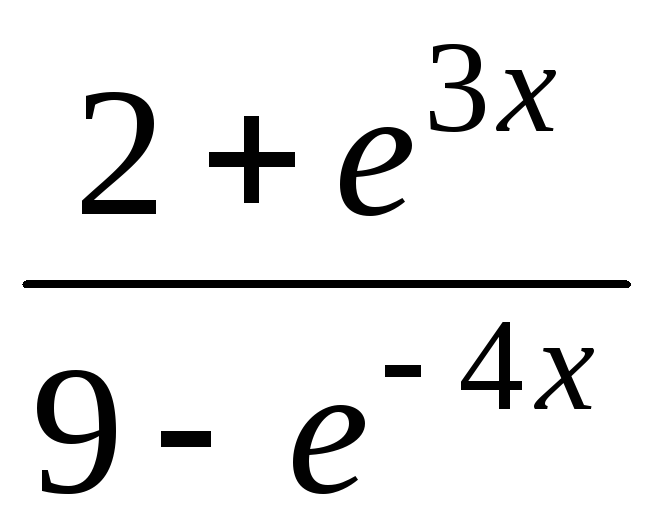 x2; ж)
у =
x2; ж)
у =