
- •Методичні вказівки
- •Затверджено на засіданні
- •Навчальне видання
- •Лабораторна робота №1 тема: Структурний аналіз механізму
- •А) б)
- •Лабораторна робота №2 тема: Дослідження головних кінематичних параметрів машини
- •Лабораторна робота №3 тема: Виготовлення зубчастих коліс методом обкатки
- •Лабораторна робота №4 тема: Обмірювання зубчастих коліс
- •Лабораторна робота №5 Тема: Зрівноваження обертальних ланок
- •Додаток
Лабораторна робота №5 Тема: Зрівноваження обертальних ланок
Мета роботи: динамічне зрівноваження складної обертальної ланки рахунковими методами (тобто на стадії проектування ланки) і перевірка зрівноваження на лабораторному пристрої ТММ-35.
Прилади:прилад ТММ-35, комплект противаг (масамиm= 40, 50, 60, 70 г), циркуль, лінійка, транспортир, калькулятор.
Теоретичні відомості
Ротором (за ДСТУ 19534-74) називають ланки механізмів, які виконують обертовий рух і утримуються при цьому своїми несучими поверхнями в опорах. Тому ротором є якір електродвигуна, колінчатий вал компресора, шпиндель токарського верстата, баланс годинника і т.п.
З теоретичної механіки відомо, що тиск тіла, що обертається, на його опори в загальному випадку складається із двох складових: статичної, викликаною дією заданих сил (сили ваги тіла й ін.), і динамічної, обумовленою прискореним рухом матеріальних часток, з яких складається обертове тіло (тобто ротор). Якщо динамічна складова не дорівнює нулю, то ротор у цьому випадку називають неврівноваженим.
При рівномірному обертанні ротора навколо осі Z (рис. 5.1) проекції динамічної складової визначаються в такий спосіб:
ХА + ХВ=ФХ,
YА+YВ=ФY,
-ХAа+ХBb = МФY,
YAa-YBb=MФX.
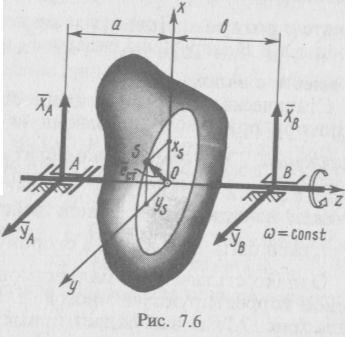
Рис. 5.1.
Як
видно, неврівноваженість чисельно
оцінюється за допомогою проекцій
головного вектора
![]() і головного моменту
і головного моменту
![]() відцентрових сил інерції ротора. Ці
проекції підраховуються за формулами:
відцентрових сил інерції ротора. Ці
проекції підраховуються за формулами:
![]() , (5.1)
, (5.1)
де, т – маса ротора;
xs, ys – проекції координати центра мас на вісі x і y;
Jyz і Jxz – відцентрові моменти інерції ротора щодо системи координат Oxyz (рис. 5.1).
Площина
Оху
проходить через центр мас S
ротора, а вся система координат Oxyz
обертається разом з ротором. Слід
відзначити, що в розглянутому динамічному
завданні головний момент сил інерції
ротора
![]() є векторною величиною.
є векторною величиною.
Як видно з рівнянь (5.1), неврівноваженість ротора зростає пропорційно квадрату його кутової швидкості. Тому якщо швидкохідні ротори (робочі колеса турбін, шліфувальні круги, магнітні барабани ЕОМ і багато інших) неврівноважені, то вони викликають динамічний тиск на свої опори, що викликають вібрацію стійки (станини) і її основи. Усунення цього шкідливого впливу називають балансуванням (зрівноважуванням) ротора. Рішення даного завдання відноситься до динамічного проектування машин.
Модуль головного вектора відцентрових сил інерції ротора, відповідно до рівнянь (5.1), можливо визначити як:
![]() .
.
У векторному виді запишемо
![]() ,
,
де r=еСТ – радіус-вектор центра мас S ротора, що координує його ексцентричне положення (рис. 5.1) і іменований ексцентриситетом маси ротора. Позначимо:
![]() . (5.2)
. (5.2)
Вектор
![]() називають головним
вектором дисбалансів
ротора. Очевидно, що
називають головним
вектором дисбалансів
ротора. Очевидно, що
![]() .
.
Модуль головного моменту відцентрових сил інерції ротора, відповідно до рівнянь (5.1), складе
![]() .
.
Де
величина
![]() називається головним
моментом дисбалансів
ротора:
називається головним
моментом дисбалансів
ротора:
![]() (5.3)
(5.3)
і
має векторне значення, тобто
![]() .
.
Надалі
неврівноваженість ротора кількісно
будемо характеризувати не через
![]() і
і
![]() ,
а через пропорційні їм головний вектор
,
а через пропорційні їм головний вектор
![]() і головний момент
і головний момент
![]() дисбалансів ротора.
дисбалансів ротора.
Види неврівноваженості ротора
Статична
неврівноваженість
властива такому ротору, центр мас S
якого не перебуває на його осі обертання,
але головна центральна вісь інерції
(вісь І–І)
якого паралельна осі обертання (рис.
5.2, а). У цьому випадку r0,
Jxz=Jyz=0.
Отже, відповідно до рівнянь (5.2)
і (5.3), статична неврівноваженість
виражається тільки головним вектором
![]() дисбалансів, у той час як головний момент
дисбалансів
дисбалансів, у той час як головний момент
дисбалансів
![]() .
Вектор
.
Вектор
![]() спрямований радіально й обертається
разом з ротором.
спрямований радіально й обертається
разом з ротором.
Прикладом
може слугувати одноколінчастий вал.
Опори А
і В
навантажені силами
![]() і
і
![]() ,
вектори яких обертаються разом з валом.
,
вектори яких обертаються разом з валом.
Статична неврівноваженість може бути усунута, якщо до ротора прикріпити додаткову масу mк яку називають коригувальною. Її треба розмістити таким чином, щоб
![]() .
.
Це
значить, що центр коригувальної маси
повинен перебувати на лінії дії OS
вектора
![]() ,
а вектор
,
а вектор
![]() повинен
бути спрямований убік, протилежну
вектору
повинен
бути спрямований убік, протилежну
вектору
![]() .
.
Однак
статичне балансування не завжди вдається
виконати однією коригувальною масою.
Так, конструкція одноколінчастого вала
(рис. 5.2, а) змушує застосувати дві маси,
розташовані в площинах корекції М
і N,
тому що простір між цими двома площинами
повинен бути повністю вільним для руху
шатуна. У цьому випадку вектор
![]() буде виражати сумарний вплив обох
коригувальних мас. Отже, число і
розташування площин корекції вибирають
згідно конструкції та призначенню
ротора.
буде виражати сумарний вплив обох
коригувальних мас. Отже, число і
розташування площин корекції вибирають
згідно конструкції та призначенню
ротора.
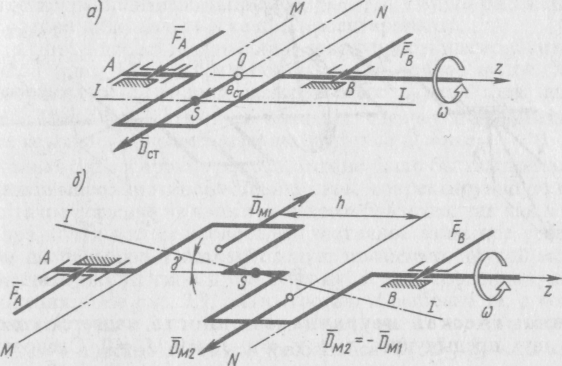
Рис. 5.2. Приклади статично (а) та моментно (б) неврівноваженого ротора
Моментна
неврівноваженість
має місце в тому випадку, коли центр мас
S
ротора перебуває на осі обертання, а
головна центральна вісь інерції І-І
ротора нахилена до осі обертання ротора
під кутом
(рис.
5.2, б). У цьому випадку r=0,
Jxz0,
Jyz0.
Отже згідно до (5.2),
![]() ,
так що моментна неврівноваженість
виражається тільки головним моментом
,
так що моментна неврівноваженість
виражається тільки головним моментом
![]() дисбалансів, тобто парою дисбалансів
дисбалансів, тобто парою дисбалансів
![]() ,
що обертається разом з ротором.
,
що обертається разом з ротором.
Прикладом
може слугувати двоколінчастий вал, для
якого MD=DM1h.
Опори А
і В
навантажені парою сил
![]() ,
вектори яких обертаються разом з валом.
,
вектори яких обертаються разом з валом.
Як
відомо пари врівноважуються тільки
парою, тому щоб усунути моментну
неврівноваженість необхідно застосувати
не менш чим дві коригувальні маси. Їх
розташування в площинах корекції і їх
величини повинні бути такими, щоб
дисбаланси коригувальних мас склали
саме пару. Момент
![]() цієї пари повинен дорівнювати
цієї пари повинен дорівнювати
![]() .
Виходить, що момент
.
Виходить, що момент
![]() повинен бути спрямований протилежно
моменту пари
повинен бути спрямований протилежно
моменту пари
![]() ,
тобто стосовно до положення ротора,
зображеному на рис. 5.2, б, – проти
годинникової стрілки.
,
тобто стосовно до положення ротора,
зображеному на рис. 5.2, б, – проти
годинникової стрілки.
Динамічна
неврівноваженість
є сукупністю двох попередніх, тобто
r0,
Jxz0,
Jyz0.
Отже,
динамічна неврівноваженість виражається
через
![]() і
і
![]() .
.
З
теоретичної механіки відомо, що така
система навантаження еквівалентна двом
перехресним векторам. Тому динамічна
неврівноваженість може бути виражена
також і іншим чином, а саме двома
перехресними векторами дисбалансів
![]() і
і
![]() ,
які розташовані у двох площинах,
перпендикулярні осі обертання, і
обертаються разом з ротором ("хрест
дисбалансів").
,
які розташовані у двох площинах,
перпендикулярні осі обертання, і
обертаються разом з ротором ("хрест
дисбалансів").
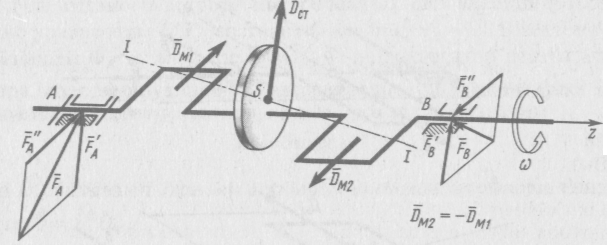
Рис. 5.3. Приклад динамічно неврівноваженого ротора
Прикладом
динамічно неврівноваженого ротора може
слугувати двоколінчастий вал з
ексцентрично закріпленим на ньому
круглим диском (рис. 5.3). Опори А
і В
навантажені перехресними силами
![]() і
і
![]() ,
вектори яких обертаються разом з валом.
,
вектори яких обертаються разом з валом.
Динамічну неврівноваженість можна усунути двома коригувальними масами, розташованими в площинах корекції, перпендикулярних осі обертання (див. нижче).
Із сказаного випливає, що ліквідація всякої неврівноваженості – і статичної, і моментної, і динамічної – має своїм результатом те, щоб головна центральна вісь інерції ротора співпадала з віссю його обертання, або аналітично:
![]() ,
,
![]() .
.
У цьому випадку ротор називають повністю врівноваженим. Відзначимо важливу властивість такого ротора: якщо ротор повністю збалансований для деякого значення кутової швидкості , то він збереже свою повну збалансованість при будь-якій іншій кутовій швидкості, як постійній, так і змінній.
Динамічне балансування роторів при проектуванні
Якщо експлуатація машини або приладу вимагає застосування повністю зрівноваженого ротора, а конструкція його така, що ротор неврівноважений (наприклад, рис. 5.2, 5.3), то зрівноваження такого ротора треба почати вже при проектуванні.
Нехай ротор являє собою сукупність декількох деталей 1, 2, 3 (рис. 5.4, а), що обертаються як одне ціле відносно вісі обертання Z. система неврівноважених мас m1, m2 i m3, розміщених у площинах 1, 2 і 3, задана координатами центрів мас Si всіх цих деталей (радіус-векторами r1, r2, r3 i кутами α1, α2, α3). Крім того положення площин А, 1, 2, 3 і В визначаються відповідно координатами z1=85 мм, z2=170 мм, z3=255 мм і l=340 мм (рис.5.4).
 Рис.
5.4. вал
з системою неврівноважених мас
Рис.
5.4. вал
з системою неврівноважених мас
Маючи у своєму розпорядженні ці відомості, можливо підрахувати дисбаланси неврівноважених мас за формулою
![]() . (5.4)
. (5.4)
Виконуючи врівноваження ротора, можна було б кожній неврівноваженій масі протиставити свою коригувальну масу. Однак таке рішення не є доцільним, тому що в системі ротора майже завжди відбувається часткове взаємне зрівноважування дисбалансів. Тому варто застосувати інший метод.
Призначимо
дві площини приведення А
і В,
перпендикулярні осі обертання z.
На рис. 5.4 площина А
віддалена від площини В
на відстань l.
Приведемо до площин А
і В
дисбаланси
![]() ,
,![]() ,
,![]() всіх
неврівноважених мас, тобто замінимо
кожен вектор дисбалансу двома, паралельними
йому і розташованими в площинах приведення
А
і В
(тобто застосуємо метод „замінюючих
мас”). Для цього використаємо формули:
всіх
неврівноважених мас, тобто замінимо
кожен вектор дисбалансу двома, паралельними
йому і розташованими в площинах приведення
А
і В
(тобто застосуємо метод „замінюючих
мас”). Для цього використаємо формули:
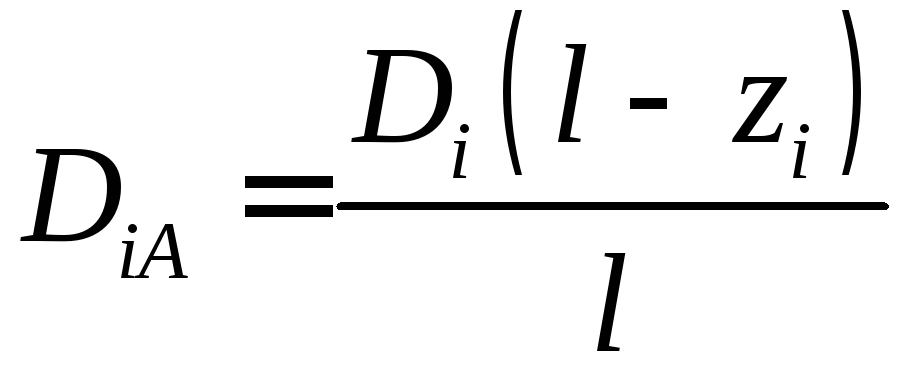 ,
,
![]() .
(5.5)
.
(5.5)
Використовуючи формули (5.5) стосовно до рис. 5.4 одержимо:
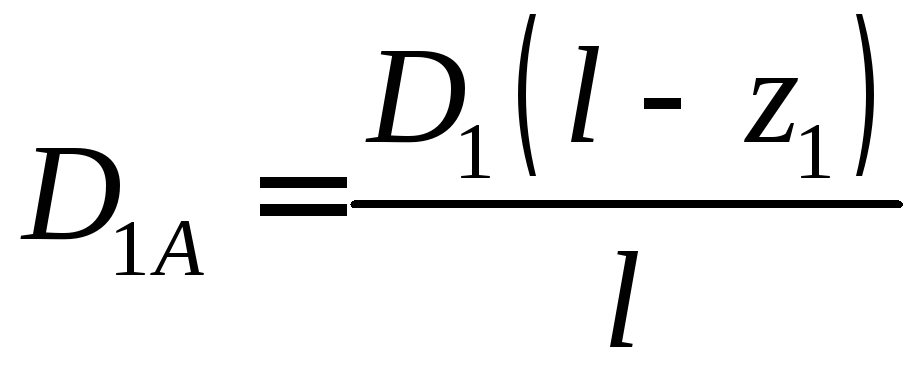 ;
;
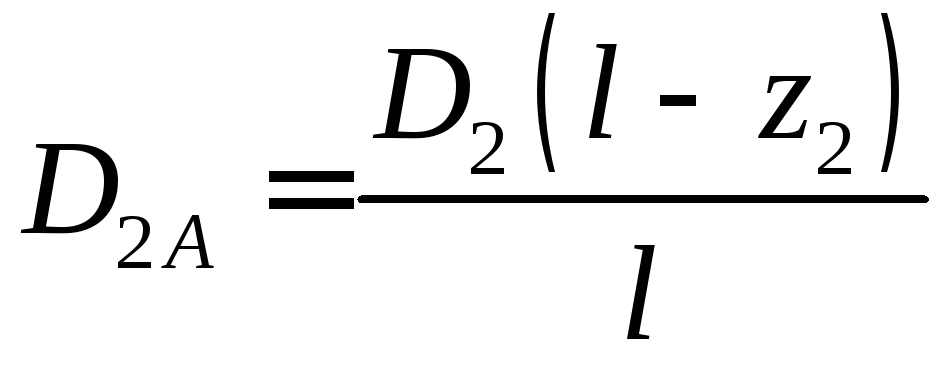 ;
;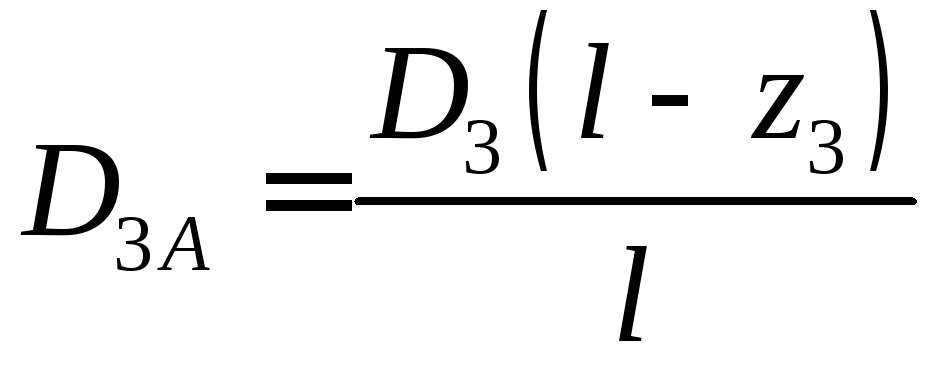 ; (5.6)
; (5.6)
![]() ;
;
![]() ;
;![]() . (5.7)
. (5.7)
У
результаті приведення просторову
систему дисбалансів
![]() ,
,![]() ,
,![]() можливо
замінити двома плоскими системами.
Складемо дисбаланси, розташовані в
кожній із площин.
можливо
замінити двома плоскими системами.
Складемо дисбаланси, розташовані в
кожній із площин.
Площина В:
![]() . (5.8)
. (5.8)
Підставимо рівняння (5.4) і (5.6) в рівняння (5.8):
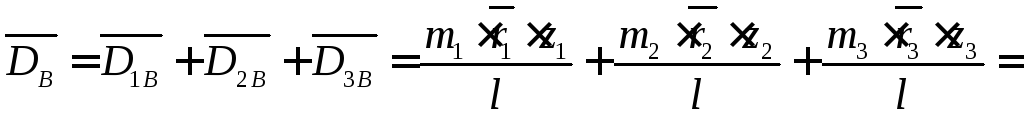
![]() . (5.9)
. (5.9)
Площина А:
![]() . (5.10)
. (5.10)
Підставимо рівняння (5.4) і (5.7) в рівняння (5.10):
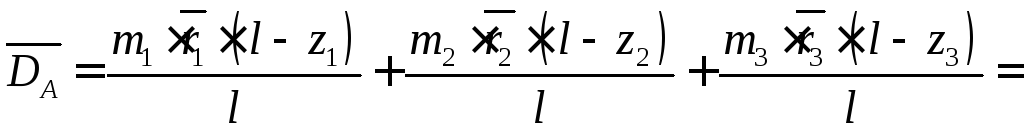
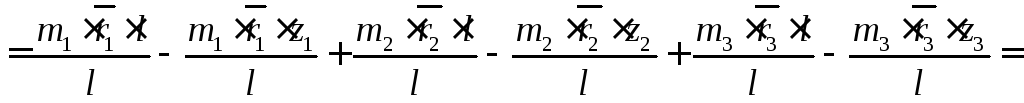
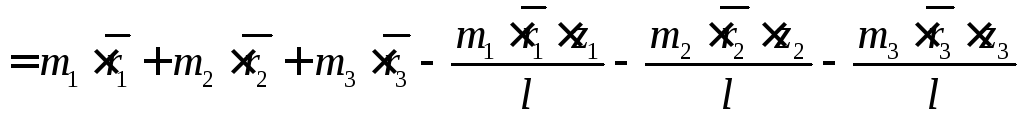 ,
,
згідно
з рівнянням (5.9) права частина рівняння
являє собою
![]() ,
тоді:
,
тоді:
![]() . (5.11)
. (5.11)
Таким
чином, неврівноваженість заданого
ротора можна представити двома
перехресними
векторами дисбалансів
![]() і
і
![]() ,
розташованими в площинах приведення А
і В.
Тому заданий ротор, як і всякий інший,
можливо збалансувати також двома
коректуючими масами. розмістимо
ці маси в площинах приведення А
і В.
Тоді вони будуть одночасно і площинами
корекції.
,
розташованими в площинах приведення А
і В.
Тому заданий ротор, як і всякий інший,
можливо збалансувати також двома
коректуючими масами. розмістимо
ці маси в площинах приведення А
і В.
Тоді вони будуть одночасно і площинами
корекції.
Умовами повного балансування будуть:
![]() ,
,
![]() . (5.12)
. (5.12)
Коригувальні маси дорівнюють:
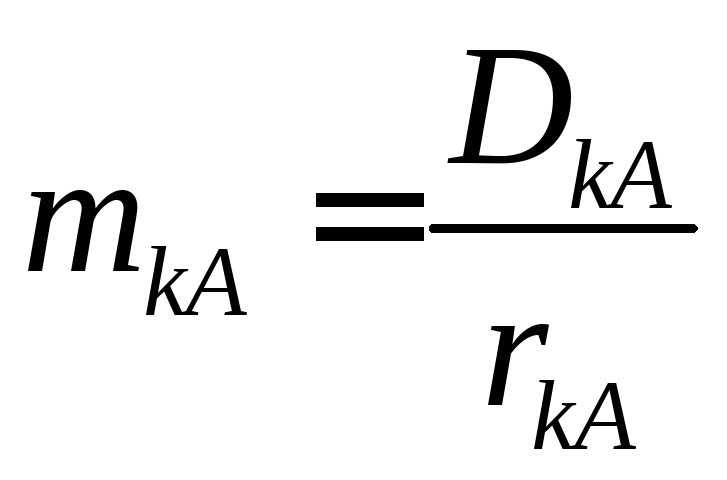 і
і
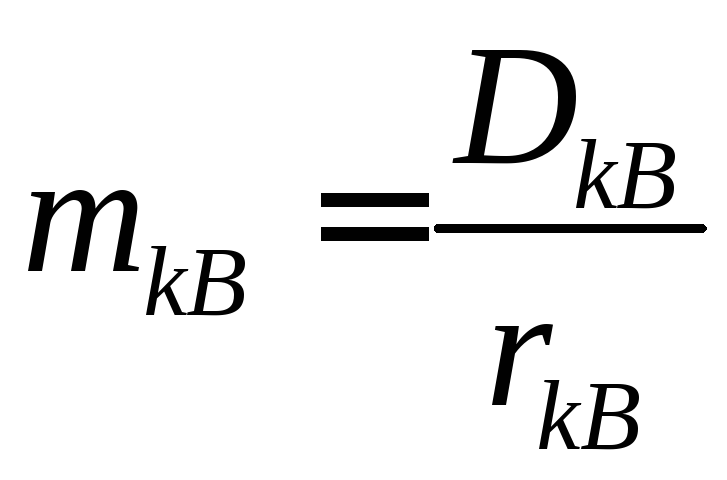 ,
(5.13)
,
(5.13)
де
![]() і
і
![]() – їх
ексцентриситети (рис. 5.4, а), призначувані
згідно конструктивним можливостям
ротора.
– їх
ексцентриситети (рис. 5.4, а), призначувані
згідно конструктивним можливостям
ротора.
Тоді згідно з рівняннями (5.10) і (5.12) з урахуванням (5.13) одержимо:
![]() ,
,
![]() ,
,
![]() ,
,
![]() . (5.14)
. (5.14)
Розрахувавши
три перші члени рівняння (5.14) (в обраному
масштабі) відкладемо відповідні відрізки
один за одним під своїми кутами (кути
вимірюємо від позитивного напрямку
вісі х).
Побудувавши многокутник векторів за
рівнянням (5.14) (рис. 5.5.), визначимо
замикаючий вектор многокутника
![]() (безпосереднім вимірюванням на
многокутнику (рис. 5.5)).
(безпосереднім вимірюванням на
многокутнику (рис. 5.5)).
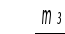
Рис. 5.5. Силовий многокутник побудований за рівнянням (5.14)
Поділивши
одержану величину на l
та задаючись масою балансира
![]() (з ряду 40, 50, 60 або 70 грам), визначаємо
радіус-вектор
(з ряду 40, 50, 60 або 70 грам), визначаємо
радіус-вектор![]() (який повинен бути в межах від 40 до 90 мм,
це пов’язано з параметрами приладуТММ-35).
(який повинен бути в межах від 40 до 90 мм,
це пов’язано з параметрами приладуТММ-35).
кутову
координату kB
варто взяти із планів дисбалансів (рис.
5.5), як кут виміряний проти годинникової
стрілки між позитивним напрямком вісі
х
та лінією, яка є продовженням вектора
![]() .
.
Для
визначення
![]() вирішимо рівняння (5.11) і (5.12) та з
урахуванням (5.13) одержимо:
вирішимо рівняння (5.11) і (5.12) та з
урахуванням (5.13) одержимо:
![]() ,
,
![]()
![]() . (5.15)
. (5.15)
Побудуємо
многокутник векторів за рівнянням
(5.15) (рис. 5.6),
визначимо замикаючий вектор
![]() .
.

Рис. 5.6. Многокутник векторів за рівнянням (5.15)
Безпосереднім
вимірюванням на многокутнику (рис. 5.6)
визначаємо вектор
![]() та задаючись величиною противаги
та задаючись величиною противаги![]() ,
визначимо радіус-вектор
,
визначимо радіус-вектор![]() .
.
кутову координату kA варто взяти із планів дисбалансів (рис. 5.6) аналогічно kB.
Усунення
неврівноваженості ротора полягає в
тому, що коригувальні маси
![]() і
і
![]() повинні бути розміщені в площинах
корекції А
и В
у місцях, обумовлених координатами kA,
повинні бути розміщені в площинах
корекції А
и В
у місцях, обумовлених координатами kA,
![]() иkB,
иkB,
![]() .
.
Відзначимо,
що замість коригувальних мас (противаг)
можна застосувати так звані "антипротиваги".
Це значить, що на лінії дії вектора
![]() розміщається не коригувальна маса, а
діаметрально протилежно їй з ротора
віддаляється відповідна кількість
матеріалу (віддаляється, як говорять,
"важке місце" ротора). Те ж саме
можна зробити й в іншій площині корекції.
Звичайно, можливість застосування
такого прийому безпосередньо визначається
конструкцією ротора.
розміщається не коригувальна маса, а
діаметрально протилежно їй з ротора
віддаляється відповідна кількість
матеріалу (віддаляється, як говорять,
"важке місце" ротора). Те ж саме
можна зробити й в іншій площині корекції.
Звичайно, можливість застосування
такого прийому безпосередньо визначається
конструкцією ротора.
Розрахунок коригувальних мас можна виконати і аналітично.
Для цього спроектуємо вектори рівняння (5.14) на вісь х, одержимо:
![]() . (5.16)
. (5.16)
з
(5.16) визначимо значення
![]() .
.
Спроектуємо вектори рівняння (5.14) на вісь у, одержимо:
![]() . (5.17)
. (5.17)
Визначимо
з (5.17) значення
![]() .
.
Кутова координата kB визначається в градусах, як:
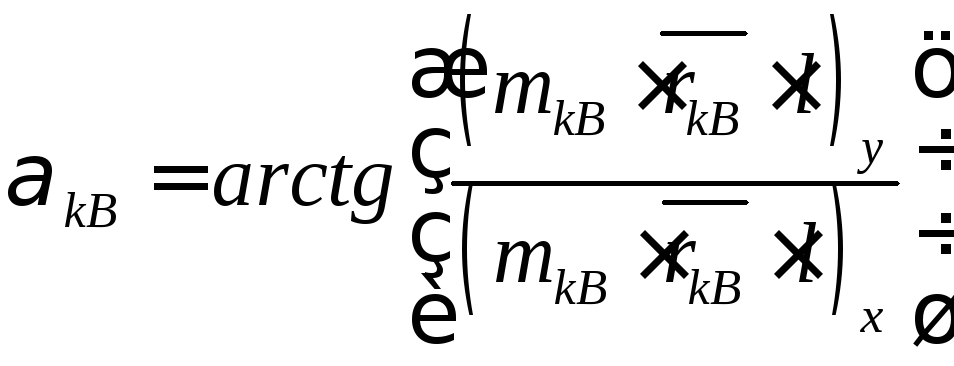 . (5.18)
. (5.18)
Радіус-вектор
![]() можливо розрахувати за формулою:
можливо розрахувати за формулою:
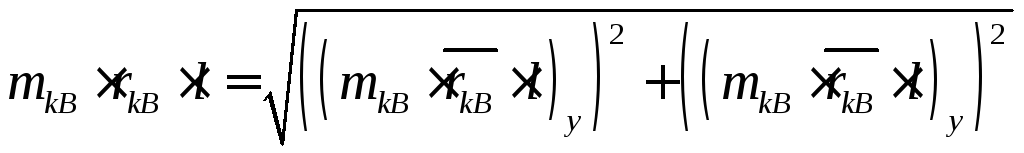 , (5.19)
, (5.19)
якщо
поділити одержану по (5.19) величину на l
та обрану масу
![]() .
.
Кутову
координату kA
та радіус-вектор
![]() можливо визначити аналогічно kB,
можливо визначити аналогічно kB,
![]() ,
якщо спроектувати на вісі рівняння
(5.15) задавшись коригувальною масою
,
якщо спроектувати на вісі рівняння
(5.15) задавшись коригувальною масою
![]() .
.
Послідовність виконання роботи:
І) Виконати теоретичні розрахунки. Для цього:
За вказівкою викладача накреслити схему установки, аналогічно рис. 5.5.
записати до звіту масу і координати неврівноважених мас згідно до табл.5.1.
Таблиця 5.1
Розрахункові дані для врівноваження
|
Назва площини |
mi, грам |
rі, мм |
αі, градуси |
zі, мм |
|
А |
|
|
|
0 |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
В |
|
|
|
|
Розрахувати величини
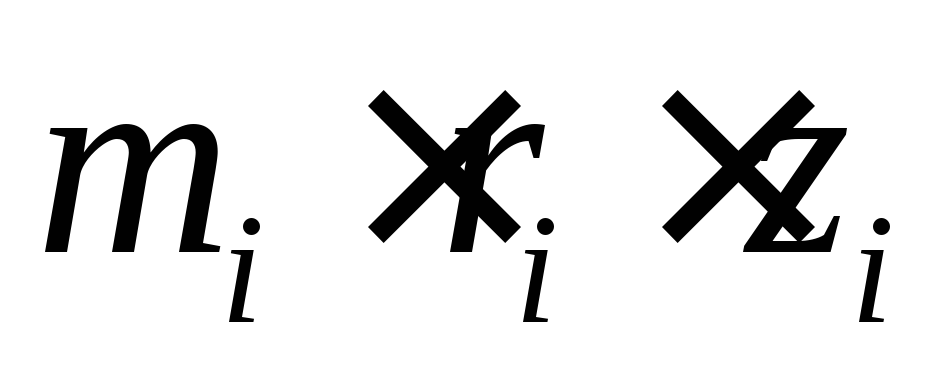 і побудувати многокутник векторів, у
обраному масштабі
і побудувати многокутник векторів, у
обраному масштабі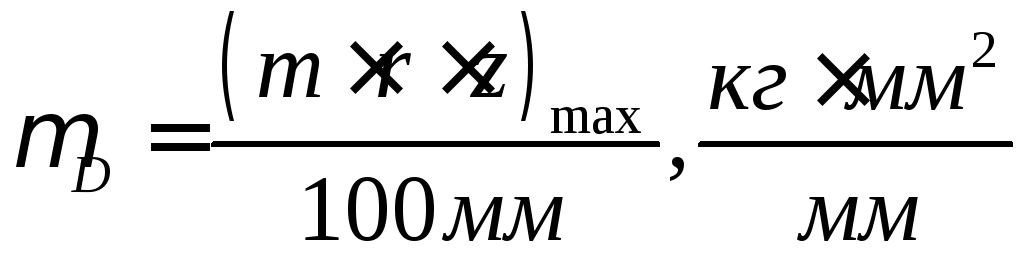 (див. рис. 5.6). За допомогою якого визначаємо
(див. рис. 5.6). За допомогою якого визначаємо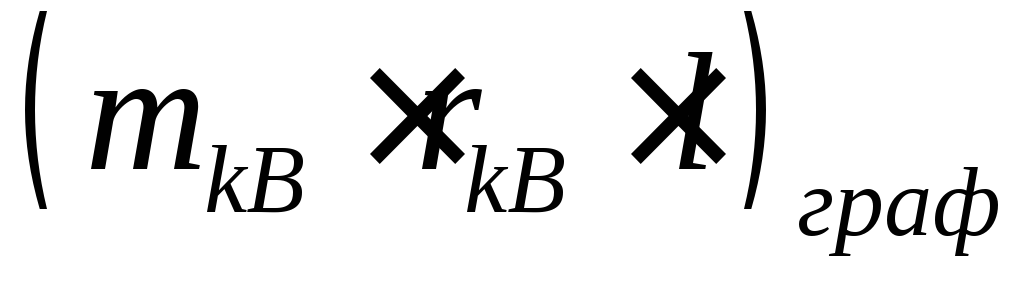 та з урахуванням масштабного коефіцієнта
знаходимо
та з урахуванням масштабного коефіцієнта
знаходимо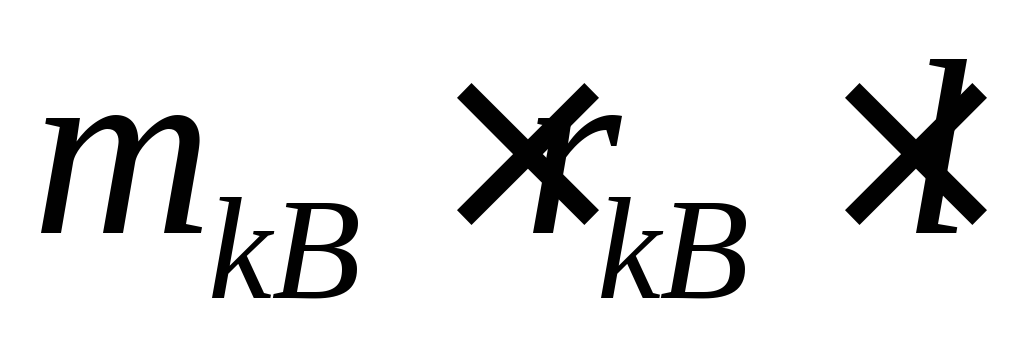 .
Задаючись масою противаги
.
Задаючись масою противаги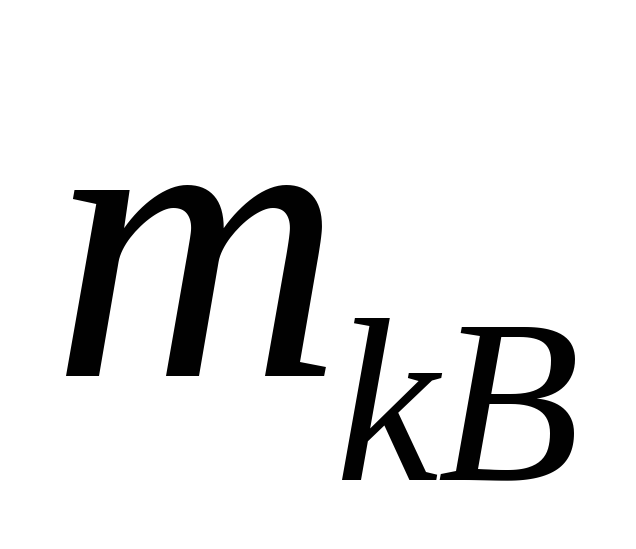 за формулою:
за формулою: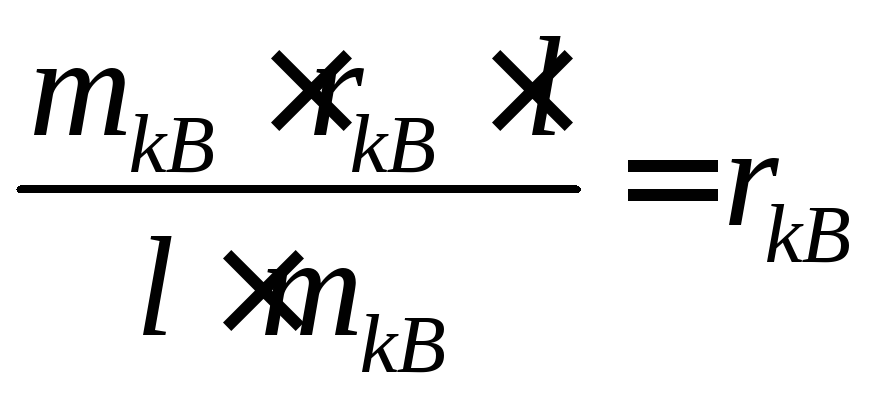 визначають
визначають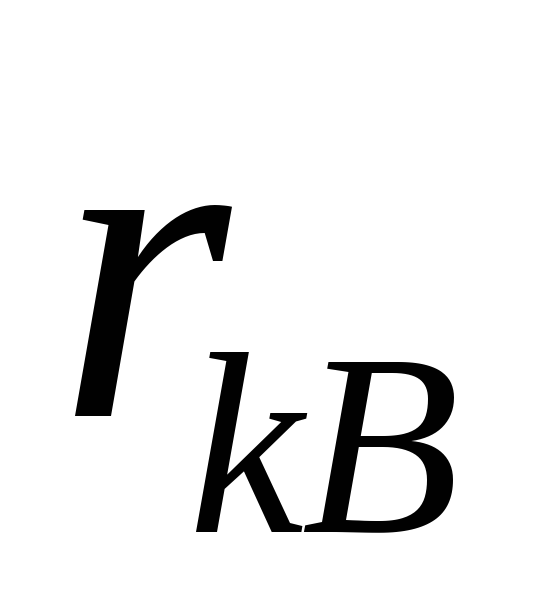 і вимірюють кутαkB
з плану дисбалансів.
і вимірюють кутαkB
з плану дисбалансів.Розрахувати величини
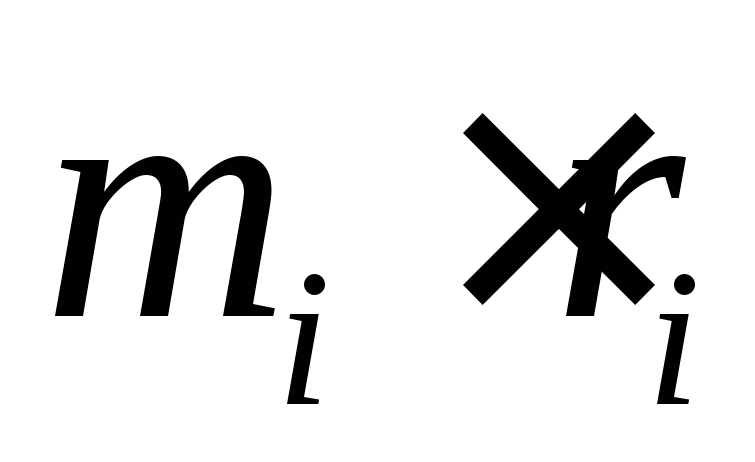 і побудувати многокутник векторів у
обраному масштабі
і побудувати многокутник векторів у
обраному масштабі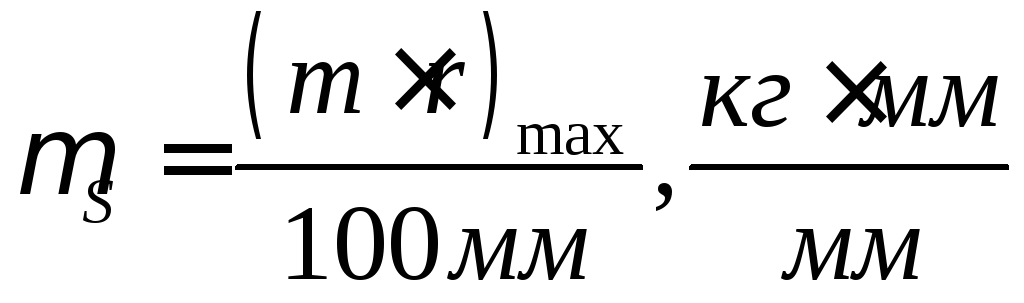 (див. рис. 5.7). Визначаємо
(див. рис. 5.7). Визначаємо та задаючись вагою
та задаючись вагою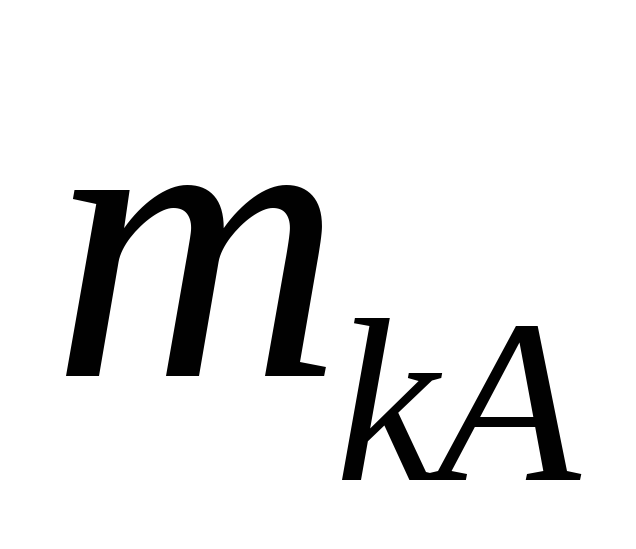 противаги, знаходимо її координату
противаги, знаходимо її координату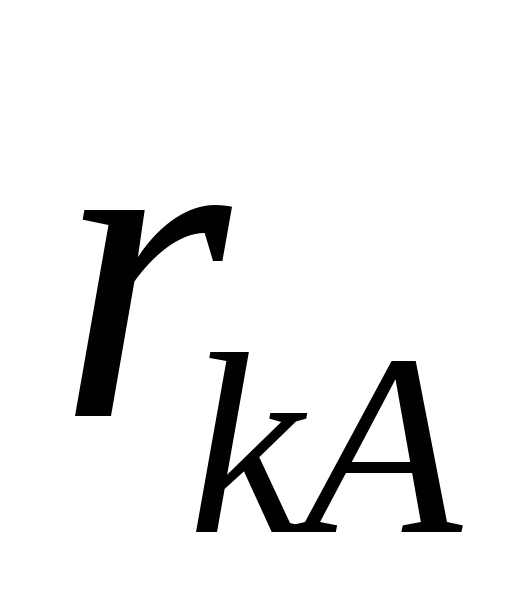
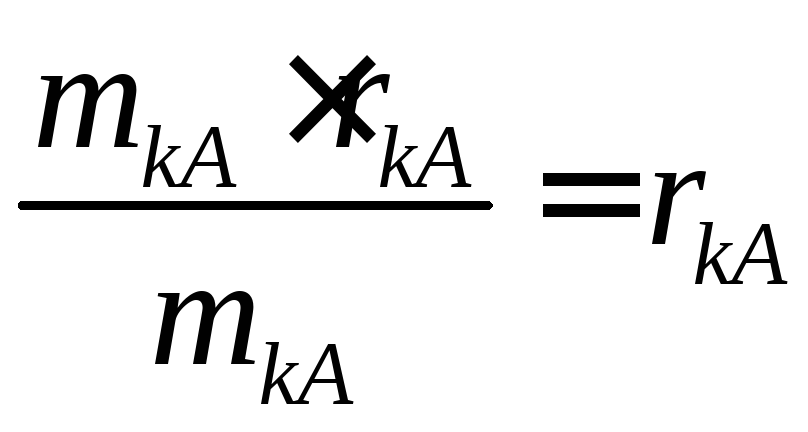 таαkА
(з плану дисбалансів).
таαkА
(з плану дисбалансів).Остаточно заповнюють табл.5.1.
ІІ) На приладі ТММ –35 виконати перевірку розрахунків. Для цього:
На приладі поставити (виставити) задані маси у відповідних площинах зі своїми координатами.
Встановити знайдені противаги масами
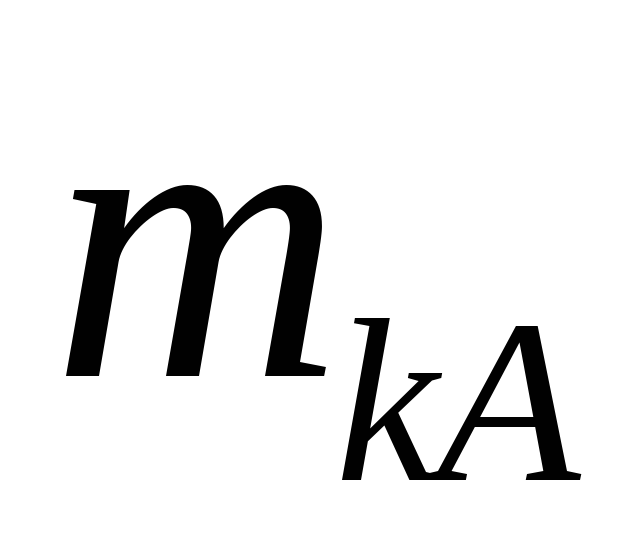 i
i
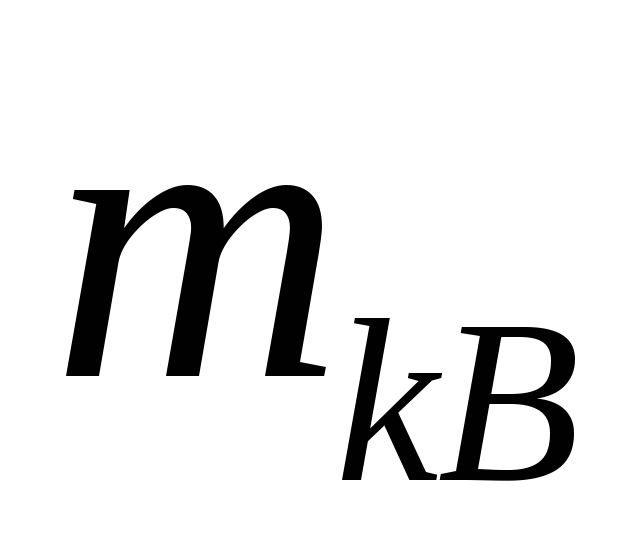 зі своїми координатами в площинах
виправлення А
і В.
зі своїми координатами в площинах
виправлення А
і В.Перевірити статистичну зрівноваженість обертальної ланки на установці, тобто при повороті обертальної ланки на будь-який кут вона повинна знаходитись у стані рівноваги, а не обертаючись шукати його.
Перевірити динамічну зрівноваженість – при розгоні і гальмуванні ланки незачеплений кінець валу не повинен мати коливання.
За результатами роботи скласти звіт і подати на перевірку викладачеві.
Зміст звіту
Схема пристрою.
Таблиця 5.1.
Векторні рівняння та розрахунки до них, визначення масштабних коефіцієнтів.
Побудовані в масштабі плани дисбалансів відносно площин В та А.
Висновки.
Контрольні питання
Поняття ротору.
Що називають неврівноваженістю?
Головний вектор та головний момент дисбалансів?
Види неврівноваженості роторів.
Умови статичної неврівноваженості та її усунення.
Умови моментної неврівноваженості та її усунення.
Умови динамічної неврівноваженості та її усунення.
Список літератури
Теория механизмов и механика машин. // Под ред. Фролова К.В. – М.: Высшая школа, 1998. – с. 189–206.
Аротоболевский И.И. Теория механизмов и машин. – М.:Наука, 1988. – с. 275–300.
Кожевников С.Н. Теория механизмов и машин. – М.:Машиностроение, 1964. – с. 545–575.
