
Пособие ТОКН
.pdf
2.6. Учет процессов старения
Учет влияния влажности, давления и ряда других внешних воздействий производится аналогично учету температуры. Несколько отличным способом производится учет старения за счет необратимого характера происходящих при этом изменений значений входных параметров. Под старением понимается коррозия, «усталость» металла, износ и др. Остановимся на этом подробнее.
Как и при учете температурных воздействий, будем считать, что на рассматриваемом интервале времени 0 ÷T характер изменения входного параметра описывается линейной моделью
xi (t) = xi0 (1 + KCX i τ) , |
(2.19) |
где KCX i , i =1,2,…,n, – коэффициент старения.
Поскольку по форме модели (2.13) и (2.19) совпадают, мы можем, не проводя выкладки, записать ряд соотношений:
коэффициент старения выходного параметра
KCY = ∑Bi KCX i ;
характеристики поля разброса коэффициента старения выходного параметра
E(KCY ) = ∑Bi E(KCYi ), |
l(KCY ) = ∑Bi2 δ2 (KCYi ) ; |
вклад временной составляющей погрешности
yy Σ = yy пр + yy t + yy τ;
расчет характеристик поля рассеивания с учетом всех составляющих
E y Σ = E y пр + E y t + E y τ, ly Σ = ly2 пр + ly2 t + ly2 τ , |
(2.20) |
где
E y τ = E(КСY ) τ, |
ly τ = l(КСY ) τ. |
Разница между температурой и старением состоит в одном: температурные изменения обратимы (если температура не превышает некоторой критической), старение необратимо, оно постоянно изменяет параметры элементов.
Как нетрудно видеть, учет старения приводит к дополнительному, причем необратимому, смещению координаты середины поля рассеивания, что дополнитель-
61
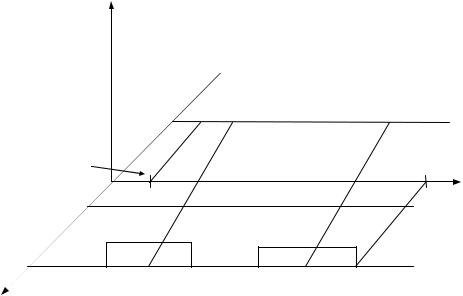
но его расширяет. Графическая иллюстрация совместного влияния трех рассмотренных погрешностей приведена на рис. 2.9; для простоты показаны равномерные законыраспределенияпогрешностей, аненормальные, какэтодолжнобыть.
Если принять в качестве границ поля рассеивания минимальное и максимальное возможные значения погрешностей выходного параметра, то расчет значений этих границ рекомендуется проводить в следующем порядке:
по формуле (2.20) рассчитываются четыре значения величины Ety,τΣ для следующих комбинаций температуры и времени (t,τ) : (t1,0) , (t2 ,0) , (t1,T ) , (t2 ,T ) ;
по формуле (2.20) рассчитываются четыре значения величины lty,τΣ для пе-
речисленных выше комбинаций температуры и времени (t,τ) ;
рассчитываются верхние и нижние границы поля рассеивания погрешности выходного параметра для перечисленных выше комбинаций:
l+t,τ = Ety,τΣ + lty,τΣ, |
l−t,τ = Ety,τΣ − lty,τΣ; |
определяются верхние и нижние границы поля рассеивания погрешности выходного параметра:
l+t,τ = max{l+t1 ,0 , l+t2 ,0 , l+t1 ,T , l+t2 ,T }, l−t,τ = min{l−t1 ,0 , l−t2 ,0 , l−t1 ,T , l−t2 ,T }.
На рис. 2.9 приведены значения этих границ для случая TKY > 0 и KCY > 0 .
ϕ( yy)
|
|
|
τ = 0 |
|
|
τ =T |
||
|
|
|
|
|
|
|||
t1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|||
lt,τ |
|
|
|
|
|
|
lt,τ |
|
|
|
|
|
|
|
|||
− |
|
|
|
|
|
|
+ |
|
200 |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
t2
t
Рис. 2.9. Совместный учет температуры и старения
62

2.7. Методы достижения заданной точности выходного параметра (синтез допусков)
Рассматриваемая ниже общая задача, обычно называемая задачей синтеза допусков, формулируется следующим образом: для заданного устройства и допуска на выходной параметр требуется определить номинальные значения параметров элементов и допуски на них. Нетрудно видеть, что эта задача не имеет однозначного решения, что позволяет нам из множества возможных решений выбрать в некотором смысле наилучшее (оптимальное). В зависимости от дополнительных условий существует несколько методов решения этой задачи. Рассмотрим их.
2.7.1. Метод полной взаимозаменяемости Суть метода состоит в том, что заданная точность выходного параметра у
всех изделий партии достигается за счет использования элементов с заданными допусками без отбора и подгонки. Таким образом, при замене любого элемента изделия на однотипный ему элемент значение выходного параметра должно сохраняться в пределах его поля допуска. Реализация этого метода предполагает, что систематическая погрешность выходного параметра отсутствует, т.е. Ey = 0 , а все возможные значения выходного параметра входят в поле допуска,
т.е. выполняется условие
δy ≥ l y = 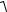 ∑Bi2 δi2
∑Bi2 δi2
(предполагается, что разброс выходного параметра рассчитывается по методу квадратичного сложения), а допуск на выходной параметр задан и равен δy .
Из этого условия ясно, что задача имеет множество решений и из них можно выбрать оптимальное. Существует много различных критериев оптимальности, в том или ином отношении характеризующих качество решения задачи синтеза. Мы рассмотрим стоимостной критерий, предполагая, что стоимость i-го параметра обратно пропорциональна его допуску:
c |
= ai |
+b , |
i=1,2,…,n, |
i |
δi |
i |
|
где ai и bi – коэффициенты, которые при необходимости можно найти методом
наименьших квадратов, располагая данными о точностных и стоимостных характеристиках элементов. Суммарная стоимость устройства – это просто сумма стоимостей отдельных элементов плюс общие затраты на изготовление устройства (сборка, регулировка и т.п.):
n |
|
ai |
|
|
|
C = ∑i =1 |
( |
|
|
+bi ) + c0 . |
(2.21) |
δ |
i |
||||
|
|
|
|
|
|
63

Таким образом, задача синтеза допусков приведена к следующей оптимизационной задаче: требуется минимизировать стоимость (2.21) при ограничении
δy ≥ 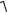 ∑Bi2 δi2 .
∑Bi2 δi2 .
Нетрудно показать (см. упражнение 8), что последнее неравенство можно заменить в нашем случае на равенство
δy = ∑Bi2 δi2 . |
(2.22) |
Полученная задача называется задачей условной оптимизации: требуется найти минимум функции (2.21) при условии (2.22). Для ее решения предлагается использовать метод множителей Лагранжа; сформулируем его в виде теоремы, которая дается без доказательства.
Теорема. Для нахождения экстремума функции
y = f (x1, x2 ,..., xn )
при ограничении
ϕ(x1, x2 ,..., xn ) = 0
строится функция Лагранжа
Φ(x1, x2 ,..., xn ) = f (x1, x2 ,..., xn ) + λϕ(x1, x2 ,..., xn ) ,
где λ – неопределенный множитель Лагранжа, и решается задача безусловной оптимизации функции Φ .
Для использования этой теоремы в нашем случае предварительно в целях упрощения вычислений возведем обе части равенства (2.22) в квадрат:
δ2y = ∑Bi2 δi2 .
Запишем функцию Лагранжа:
n |
a |
i |
|
+ λ(∑Bi2 δi2 −δ2y ) . |
Φ(δ1, δ2 ,..., δn ) = ∑( |
|
+bi ) + c0 |
||
|
|
|||
i =1 |
δi |
|
||
Для определения точки минимума этой функции найдем частные производные по допускам δ1,δ2 ,...,δn и множителю λ, приравняем их нулю и решим по-
64
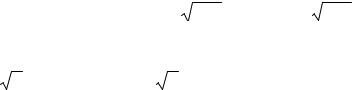
лученную систему уравнений. Можно показать (упражнение 9), что это решение и будет являться решением исходной задачи. Проделаем необходимые выкладки:
|
∂Φ |
= − |
ai |
+ 2λB2 |
δ |
i |
= 0 , |
|
|
|
(2.23) |
|||
|
|
|
|
|
|
|
||||||||
|
∂δi |
|
δi2 |
i |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
∂Φ |
= ∑Bi2 δi2 −δ2y |
|
= 0 . |
|
|
|
(2.24) |
|||||
|
|
∂λ |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение системы уравнений в общем виде весьма громоздко, потому |
||||||||||||||
ограничимся частным случаем, когда n = 2 , |
B1 =1/ 2 , B1 =1/ 3 , a1 = 4 , a2 = 6 . |
|||||||||||||
В этом случае из (2.23) и (2.24) следует δ |
|
= 2 3 1/ λ |
и δ |
2 |
= 3 3 |
1/ λ , что в |
||||||||
итоге дает |
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
δ1 = 2 δy , |
δ2 = (3/ 2) δy . |
|
|
|
|
|||||||||
Сравнивая полученный результат с коэффициентами влияния B1 =1/ 2 и B1 =1/ 3 , можно сделать вывод о том, что чем меньше коэффициент влияния,
тем больше допуск на соответствующий параметр, что хорошо согласуется с интуитивным понимаем того, как входные параметры влияют на выходной.
Недостатком метода является то, что он слишком дорог – даже минимизация общих затрат не спасает дела.
2.7.2. Метод неполной взаимозаменяемости Суть метода состоит в том, что заданная точность выходного параметра у
части изделий партии достигается за счет использования элементов с заданными допусками без отбора и подгонки. Таким образом, уже не требуется, чтобы после замены любого элемента изделия на однотипный ему элемент значение выходного параметра всегда оставалось в пределах его поля допуска; у некоторых изделий это значение может выйти за допуск. При этом возникает необходимость в доработке таких изделий, если это возможно; при отсутствии такой возможности изделие бракуется. Рассмотрим оба случая, предполагая, что
Ey = 0 , а ограничение (2.22) отсутствует.
1.Доработка возможна. Предполагается, что стоимость доработки одного изделия равна сд. В качестве критерия оптимальности здесь предлагается ис-
пользовать средние затраты на изготовление и доработку изделий:
CΣ = N C + Nд сд,
где N – объем изготовленной партии изделий; Nд – число изделий, которые нуждаются в доработке, оно определяется числом N и долей изделий α , выходной
65

параметр у которых оказался за пределами поля допуска: Nд = Nα. Она равна площади заштрихованных участков на рис. 2.6 и определяется интегралом
α = |
2 |
∞ |
−z 2 / 2σ2y |
dz = |
2 |
∞ |
−x2 |
/ 2 |
dx |
|
∫e |
|
|
∫e |
|
|
|||
|
2π δy |
|
|
2π δy / σy |
|
|
|||
(последнее преобразование выполнено с помощью подстановки x = z / σy ). До-
пуски, подлежащие определению, входят в выражение для среднего квадратического σy :
σy = 13 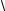 ∑Bi2 δi2 .
∑Bi2 δi2 .
Витоге критерий оптимальности принимает следующий вид:
C |
|
= N ( |
n |
( |
ai |
+b ) + c |
|
) + |
2Ncд |
∞ |
−x2 |
/ 2 |
dx → min . |
(2.25) |
|
∑i =1 |
|
|
|
e |
|
|
|||||||
|
Σ |
|
|
δi |
i |
0 |
|
2π |
δy /∫σy |
|
|
|
||
Решение задачи может быть осуществлено с помощью численных методов, поскольку использование производных приводит к системе трансцендентных уравнений.
2. Доработка невозможна, изделие идет в брак. В качестве критерия оптимальности в этом случае предлагается принять размер ожидаемой прибыли от реализации годных изделий, число которых определяется формулой
Nг = N(1 −α) .
Ожидаемая прибыль П – это разность между ожидаемым уровнем реализации и затратами на изготовление партии изделий:
П = NгЦ − NС,
где Ц – рыночная цена изделия. После несложных вычислений получаем:
|
2NЦ δy |
−x2 / 2 |
n |
ai |
|
|
П = |
2π 0∫ e |
|
dx − N (∑i=1( |
δi |
+ bi ) + c0 ) → max . |
(2.26) |
Как и в предыдущем случае, решение может быть найдено с помощью численных методов. Можно показать (предлагается сделать это самостоятельно), что задачи (2.25) и (2.26) эквивалентны, если заменить в (2.26) цену Ц на сд.
66
2.7.3. Метод подгонки Суть метода состоит в том, что заданная точность выходного параметра у
конкретного изделия достигается путем подбора одного из схемных элементов. Таким образом, значения одного или нескольких элементов подбираются так, чтобы получить необходимое (т.е. находящееся в допуске) значение выходного параметра.
2.7.4. Метод регулировки Суть метода состоит в том, что заданная точность выходного параметра у
конкретного изделия достигается путем введения в схему подстраиваемых элементов. Таким образом, необходимое значение выходного параметра также достигается за счет схемных элементов, только в отличие от предыдущего случая здесь используются подстраиваемые элементы, значения параметров которых могут меняться в определенных пределах.
Недостатком метода является то, что надежность подстраиваемых элементов несколько ниже, чем элементов с постоянными параметрами, кроме того, они дороже.
2.7.5. Точный метод назначения допусков Методы синтеза допусков, рассмотренные в пп. 2.7.1 и 2.7.2, предполагают
возможность линейной аппроксимации зависимости y = f (x1, x2,..., xn ) . Такое
допущение позволяет существенно упростить поиск решения задачи, но в ряде ситуаций приводит к значительным ошибкам в результатах расчета. Вместе с тем для устройств невысокой сложности с помощью метода неопределенных множителей Лагранжа можно получить точное аналитическое решение задачи синтеза допусков, не прибегая к линеаризации функции y = f (x1, x2,..., xn ) .
Для более сложных устройств такое решение может быть найдено с помощью ЭВМ методами математического программирования. При этом задача
синтеза допусков ставится как |
x2 |
|
|
|
задача вписания ортогонального |
y |
|
||
параллелепипеда в область рабо- |
• |
y |
||
тоспособности исходя из условия |
|
|
|
|
требуемой точности |
выходного |
• |
|
|
параметра и некоторого критерия |
y |
|
||
|
y |
|||
оптимальности. Под |
областью |
|
||
|
|
|
||
работоспособности |
понимается |
|
|
|
часть пространства |
параметров |
|
|
|
x1, x2,..., xn , обладающая сле- x1 |
|
|
дующим свойством: если значе- |
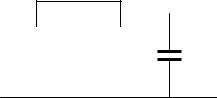
Рис. 2.10. Область работоспособности |
|
ния параметров таковы, что со- |
||
|
ответствующая им точка находится в этой области, то значение выходного параметра находится в допуске (будем обозначать это в виде y y ); если точка
лежит вне области, то и значение выходного параметра выходит за допуск. На рис. 2.10 показана эта область для двух входных параметров.
67
Ребра вписанного параллелепипеда определят допуски на параметры x1, x2,..., xn . В качестве критерия оптимальности здесь может быть задан любой
функционал от этих параметров, в частности характеризующий объем, периметр и другие характеристики вписанного параллелепипеда. При этом если взять параллелепипед максимального периметра с весами, соответствующими коэффициентам ai в формуле (2.21), то это даст решение задачи синтеза допус-
ков по стоимостному критерию (как и в п. 2.7.1), но полученное без использования процедуры линеаризации функции y = f (x1, x2,..., xn ) и, следовательно,
без внесения дополнительных погрешностей в результаты расчета. Формально задача вписания оптимального ортогонального параллелепипе-
да может быть записана как задача математического программирования вида
J = J (x1, x2 ,..., xn ) → opt
при ограничении
y = f (x1, x2 ,..., xn ) y ,
где J – выбранный критерий оптимальности. Нетрудно заметить, что решение поставленной задачи полностью определяет размеры допусков на параметры x1, x2,..., xn исходя из требований заданной точности. Оно включает в себя все
возможные виды погрешностей параметров – технологические, температурные, вызванные износом, старением и т.п.
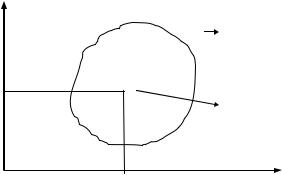
В качестве примера применения описанной методики рассмотрим задачу назначения допусков на параметры RC-цепочки 
 (рис. 2.11). Выходным параметром данного уст-
(рис. 2.11). Выходным параметром данного уст-
R ройства является постоянная времени τ = RC , на величину которой заданы ограничения τ1 ≤τ ≤τ2 .
Предполагается, что технологические возможности производства RC-цепочки могут быть сведены к требованию соблюдения соответствия между до-
пусками на величины сопротивления резистора R и емкости конденсатора C в виде δR = k δC , где k – константа. При этом задача определения допусков δR и δC
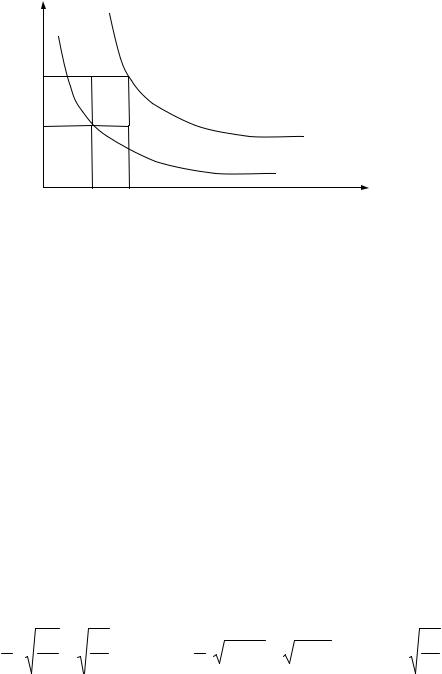
может быть решена как задача вписания максимального по площади прямоугольника с заданным соотношением сторон в область, ограниченную двумя гиперболами с заданными постоянными времени τ1 и τ2 (рис. 2.12).
Решение данной задачи можно найти аналитически, воспользовавшись методом неопределенных множителей Лагранжа, следующим образом. В качестве критерия оптимальности принимается площадь прямоугольника S = δR δC .
Ограничения, определяемые постановкой задачи, имеют вид
τ1 = R1С1, |
τ2 = R2С2 = (R1 + 2δR )(С1 + 2δC ) , |
δR = k δC . |
68
R
R2 |
|
R1 |
τ2 |
|
τ1 |
C1 C2 |
C |
Рис. 2.12. Построение вписанного прямоугольника
Преобразуем второе ограничение с учетом первого:
|
|
τ |
|
|
|
τ2 |
|
1 |
|
+ 2δC ) , |
δR = k δC . |
|
|||||
= C |
+ 2δR (С1 |
||||
|
|
1 |
|
|
|
Введение этих ограничений в целевую функцию с помощью множителей Лагранжа дает следующее выражение для поиска оптимальных значений δR и δC :
|
|
τ |
|
|
|
S = δR δC +λ1(τ2 |
|
1 |
|
+ 2δC )) +λ1(δR −k δC ) , |
(2.27) |
|
|||||
− C |
+ 2δR (С1 |
||||
|
|
1 |
|
|
|
где λ1 и λ2 – множители Лагранжа. Дифференцирование функции (2.27) по неизвестным параметрам δR , δC , C1, λ1, λ2 и приравнивание полученных со-
отношений нулю дает систему из пяти алгебраических уравнений, решением которой являются выражения
δ = |
1 |
|
τ2 |
− |
τ1 |
|
, |
δ |
|
= |
1 |
( |
τ k − |
τ k ), |
C = |
τ1 |
. (2.28) |
|
|
|
|||||||||||||||
C |
2 |
|
k |
|
k |
|
|
|
R |
|
2 |
|
2 |
1 |
1 |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полученные решения определяют точное решение задачи назначения допусков на величины параметров R и С. Для получения решения в относительных погрешностях должны быть найдены номинальные значения сопротивления и емкости. Их выбор составляет часть задачи синтеза допусков и завершает ее решение.
Решение задачи определения номинальных значений параметров является наиболее сложным как в теоретическом, так и в вычислительном аспектах. Именно на этом этапе возникает необходимость учета информации о влиянии дестабилизирующих факторов на параметры. Устройство должно быть спроектировано таким образом, чтобы исключить выход параметров элементов за
69
пределы назначенных допусков в течение требуемого времени. Иными словами, изменение этих параметров под воздействием дестабилизирующих факторов (технологического разброса, температурного дрейфа, старения) не должно выходить за область работоспособности. Детальное изложение этих вопросов выходит за пределы настоящего учебного пособия, частично они освещены [1].
2.8. Специальные методы анализа и синтеза допусков
Основой для назначения допусков аналитическими методами является
представление в каком-либо виде (явном или неявном) |
зависимости |
y = f (x1, x2,..., xn ) , что позволяет с использованием условия y |
y построить |
область работоспособности в пространстве входных параметров. Вписание в эту область ортогонального параллелепипеда полностью решает задачу синтеза допусков. Зависимость y = f (x1, x2,..., xn ) может быть получена в результате
решения уравнений, описывающих функционирование устройства. При этом для существенно нелинейных и сложных устройств построение этой зависимости, а следовательно, и области работоспособности нередко бывает связано со значительными вычислительными трудностями. Естественной альтернативой аналитическому исследованию при синтезе допусков является математическое моделирование.
Суть такого моделирования состоит в проведении ряда экспериментов – варьировании параметров элементов реального устройства до нарушения условия y y , и в итоге дает описание модели работоспособности в про-
странстве входных параметров. Наиболее известными методами математического моделирования, применяемыми при назначении допусков, являются методы граничных и матричных испытаний. До начала широкого внедрения ЭВМ в практику проектирования технических систем эти методы использовались при физическом моделировании, когда испытаниям подвергалась реальная система.
2.8.1. Метод граничных испытаний Он связан с представлением области работоспособности в виде совокупно-
сти сечений, каждое из которых является плоской кривой, полученной при варьировании двух выделенных параметров и фиксации остальных в их номинальных значениях. Последовательность проведения граничных испытаний можно описать следующим образом.
Один из входных параметров принимается за так называемый параметр граничных испытаний xг, который присутствует во всех сечениях. В качестве xг це-
лесообразно выбирать такой параметр, изменения которого в наибольшей степени влияют на выполнение (или невыполнение) условия y y . Далее выбирается
второй параметр, который должен присутствовать в требуемом сечении. Остальным параметрам придают номинальные значения и фиксируют на время получения данного сечения. Выбранному параметру придается некоторое значение, при
70
