
Higher_Mathematics_Part_2
.pdf
19. |
x − 3 |
x2 + 2x + 5 − ln x + 1+ x2 + 2x + 5 + C . |
20. − |
1 ln x + 6 + |
|
60x − 15x2 |
+ C . |
||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
15 |
2x − 3 |
|
|
||||
21. |
|
|
6x − 8 − x2 |
|
x − 2 |
+ C . 23. Remark. Use a substitution |
1 |
= t . |
|
||||||||||||||
− |
|
2(x − 2) |
+ 2 6x − 8 − x2 |
|
|
|
|||||||||||||||||
|
|
x − 1 |
|
||||||||||||||||||||
24. |
|
− ln |
|
+ |
1 |
+ |
|
x2 + x + 1 |
|
+ C . |
26. Remark. Use a |
substitution |
|
1 |
|
= t . |
30. |
Remark. |
|||||
|
1 |
|
|
|
|||||||||||||||||||
|
x |
2 |
|
x |
|
|
|
x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x2 − 1 . |
|
|
|
|
|
|
|
||||||||||
Multiple both numerator and denominator by x + |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Т.5 |
|
|
|
|
|
Individual test problems |
|
|
|
|
|
|
|
|
||||||
5.1. Find the integrals.
5.1.1. ∫ |
|
dx |
|
|
|
. |
|
|||
4 |
+ 8x − x2 |
|
|
|
||||||
|
|
|
|
|
|
|||||
5.1.4. ∫ |
|
dx |
|
|
|
. |
|
|||
x |
2 + 6x + 8 |
|
|
|
||||||
|
|
|
|
|
|
|||||
5.1.7. ∫ |
|
dx |
|
|
|
. |
|
|||
2 |
− 2x − x2 |
|
|
|
||||||
|
|
|
|
|
|
|||||
5.1.10. ∫ |
|
|
dx |
|
|
|
. |
|||
|
2x |
+ 3 − x2 |
|
|||||||
|
|
|
|
|
||||||
5.1.13. ∫ |
|
|
dx |
|
|
|
. |
|||
|
4x |
2 − x + 4 |
||||||||
|
|
|
|
|||||||
5.1.16. ∫ |
|
|
dx |
|
|
|
. |
|||
3x |
+ 2 − x2 |
|
||||||||
|
|
|
|
|||||||
5.1.19. ∫ |
|
|
dx |
|
|
|
. |
|||
16x2 |
− 8x + 3 |
|||||||||
|
|
|
||||||||
5.1.22. ∫ |
|
|
dx |
|
|
|
|
|||
|
4x |
2 + 4x + 3 |
||||||||
|
|
|
||||||||
5.1.25. ∫ |
|
|
dx |
. |
|
|||||
1 − x − x2 |
|
|||||||||
|
|
|
|
|
|
|||||
5.1.28. ∫ |
|
|
|
dx |
|
|
. |
|
||
|
3x2 |
+ 6x + 9 |
|
|
|
|||||
|
|
|
|
|
|
|||||
5.1.2. ∫ |
|
|
|
dx |
. |
|
|
|
|
||
|
x |
2 − 4x + 1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||
5.1.5. ∫ |
|
|
|
|
dx |
|
. |
|
|||
|
2 |
+ 8x − 2x2 |
|
||||||||
|
|
|
|
|
|
||||||
5.1.8. ∫ |
|
|
|
dx |
|
. |
|
|
|
|
|
1 |
+ 6x − x2 |
|
|
|
|
||||||
|
|
|
|
|
|
||||||
5.1.11. ∫ |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
4x2 − 8x + 3 |
|||||||||
|
|
|
|
||||||||
5.1.14. ∫ |
|
|
|
|
dx |
|
|
|
|
. |
|
|
|
2 |
+ 4x − x2 |
|
|
||||||
|
|
|
|
|
|
|
|||||
5.1.17. ∫ |
|
|
|
|
dx |
|
|
|
|
. |
|
|
|
2x2 |
− 8x + 10 |
|
|
||||||
|
|
|
|
|
|
|
|||||
5.1.20. ∫ |
|
|
|
dx |
|
. |
|
|
|
||
|
|
x |
2 − x + 1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
. 5.1.23. ∫ |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
5 |
− 6x − 9x2 |
|
|||||||
|
|
|
|
|
|||||||
5.1.26. ∫ |
|
|
|
|
dx |
|
|
. |
|
||
|
|
|
1 − 2x − x2 |
|
|
||||||
|
|
|
|
|
|
|
|
||||
5.1.29. ∫ |
|
|
|
|
dx |
|
. |
|
|
|
|
|
|
|
3 |
− x − x2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
141 |
|
|
|
|
|
|
|
||||
5.1.3. ∫ |
|
|
|
|
dx |
. |
|||||
|
|
|
|
|
|
||||||
|
|
2 |
− 3x − 2x2 |
||||||||
|
5.1.6. ∫ |
|
|
|
|
dx |
. |
||||
|
|
|
|
|
|
|
|||||
|
|
3 |
+ 2x − x2 |
||||||||
|
5.1.9. ∫ |
|
|
|
|
|
dx |
. |
|||
|
|
|
|
|
|
|
|||||
|
|
|
x2 − 10x + 4 |
||||||||
. |
5.1.12. ∫ |
|
|
|
|
dx |
. |
||||
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
+ 2x − x2 |
|||||
|
5.1.15. ∫ |
|
|
|
|
|
dx |
. |
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
x2 + 2x + 4 |
||||||
|
5.1.18. ∫ |
|
|
|
|
|
dx |
. |
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
x2 − 5x + 6 |
||||||
|
5.1.21. ∫ |
|
|
|
|
|
dx |
|
. |
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 − x − 2x2 |
||||||
. |
5.1.24. ∫ |
|
|
dx |
. |
||||||
|
|
|
|||||||||
|
|
|
|
|
3x − 2x2 |
||||||
|
5.1.27. ∫ |
|
|
|
|
dx |
|
|
. |
||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
4 |
− 3x − x2 |
|||||
|
5.1.30. ∫ |
|
|
|
|
dx |
|
|
|
. |
|
|
|
|
x |
2 |
+ 4x |
|
|||||
|
|
|
|
|
|
+ 8 |
|
|
|||
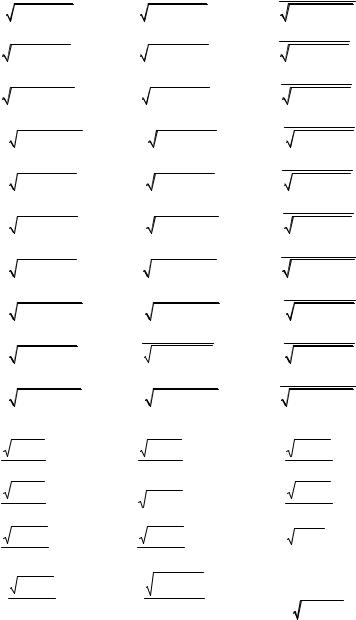
5.2. Find the integrals. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
5.2.1. ∫ |
|
(3x − 1)dx |
. |
|
|
5.2.2. ∫ |
|
|
|
|
(4x + 3)dx |
. |
|
|
|
|
|
|
5.2.3. ∫ |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
x2 + 4x + 5 |
|
|
|
|
|
|
|
7 − 2x − x2 |
|
|
|
|
|
|
|
||||||||||
5.2.4. ∫ |
|
(7x − 3)dx |
. |
|
|
|
|
5.2.5. ∫ |
|
|
|
|
|
(3 − x)dx |
. |
|
|
|
|
|
|
5.2.6. ∫ |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
6 + 2x − x2 |
|
|
|
|
|
|
|
x2 + 2x + 2 |
|
|
|
|
|
|
|
||||||||||
5.2.7. ∫ |
|
(x + 3)dx |
. |
|
|
5.2.8. ∫ |
|
|
|
|
(2x − 1)dx |
. |
|
|
|
|
|
5.2.9. ∫ |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
x2 + 8x + 18 |
|
|
|
|
|
|
|
x2 + 2x + 3 |
|
|
|
|
|
|
|
||||||||||
5.2.10. ∫ |
(5x + 4)dx |
|
. |
5.2.11. ∫ |
|
(x + 2)dx |
. |
5.2.12. ∫ |
||||||||||||||||||||
x2 + 8x + 17 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 − 2x − x2 |
|
|
|
|
|
|
|
|||||||||||
5.2.13. ∫ |
(3x + 2)dx |
. |
|
5.2.14. ∫ |
|
(6x + 1)dx |
. |
5.2.15. ∫ |
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
5 − 4x − x2 |
|
|
|
|
|
|
|
x2 + 2x + 9 |
|
|
|
|
|
|
|
||||||||||
5.2.16. ∫ |
(4 − x)dx |
. |
|
5.2.17. ∫ |
|
(7x + 4)dx |
. |
5.2.18. ∫ |
||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
x2 + 2x + 4 |
|
|
|
|
|
|
|
11− 4x − x2 |
|
|
|
|
|
|
|
||||||||||
5.2.19. ∫ |
(4x + 3)dx |
. |
|
5.2.20. ∫ |
|
|
|
(3x − 7)dx |
. |
5.2.21. ∫ |
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
3 + 2x − x2 |
|
|
|
|
|
|
|
12 + 4x − x2 |
|
|
|
|
|
|
|
||||||||||
5.2.22. ∫ |
(2 − x)dx |
|
. |
5.2.23. ∫ |
|
|
(x − 4)dx |
. |
5.2.24. ∫ |
|||||||||||||||||||
14 − 4x − x2 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 + 8x + 20 |
|
|||||||||||||||||
5.2.25. ∫ |
(5 − x)dx |
. |
|
5.2.26. ∫ |
|
dx |
. |
|
5.2.27. ∫ |
|||||||||||||||||||
|
|
|
1 − 2x − x2 |
|
||||||||||||||||||||||||
|
|
|
x2 + 4x + 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
5.2.28. ∫ |
(x + 3)dx |
|
. |
5.2.29. ∫ |
|
|
(3x + 2)dx |
. |
5.2.30. ∫ |
|||||||||||||||||||
21− 8x − x2 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 + 4x + 10 |
|
|||||||||||||||||
5.3. Use trigonometric substitution to find the integrals.
(5x + 2)dx |
. |
|
x2 + 6x + 10 |
||
|
||
(2 − 3x)dx . |
|
|
x2 − 4x + 6 |
|
|
(4x + 3)dx . |
|
|
6 − 4x − x2 |
|
(3x − 5)dx . x2 + 4x + 8 (3x + 1)dx . 8 − 4x − x2
(9x + 1)dx . |
||
5 − 2x − x2 |
|
|
(3x − 1)dx |
. |
|
x2 + 6x + 11 |
||
|
||
(3 − 4x)dx . x2 + 4x + 7 (− x + 5)dx .
x2 + 2x + 9 |
|
|
(x − 4)dx |
. |
|
13 − 6x − x2 |
||
|
5.3.1. ∫ |
1 − x |
2 |
dx . |
5.3.2. ∫ |
x2 − 1 |
dx . |
5.3.3. ∫ |
4 + x |
2 |
dx . |
|||||||||
x |
|
x |
|
|
|
x |
|
|
|||||||||||
5.3.4. ∫ |
1 − x |
2 |
dx . |
5.3.5. ∫ |
4 − x |
2 |
dx . |
5.3.6. ∫ |
x2 + 9 |
dx . |
|||||||||
x |
4 |
|
|
|
|
x |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5.3.7. ∫ |
x2 + 4 |
dx . |
5.3.8. ∫ |
4 − x2 |
dx . |
5.3.9. ∫ |
|
9 |
− x2 |
|
dx . |
||||||||
x |
2 |
|
x |
4 |
|
|
|
x |
4 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5.3.10. ∫ |
x2 + 4 |
|
5.3.11. ∫ |
(4 − x2 )3 |
5.3.12. ∫ |
|
|
dx |
|
|
|||||||||
|
x4 |
|
|
dx . |
|
x6 |
dx . |
|
|
. |
|||||||||
|
|
|
|
|
(x2 + 1)5 |
||||||||||||||
|
|
|
|
|
|
|
142 |
|
|
|
|
|
|
|
|
|
|
|
|
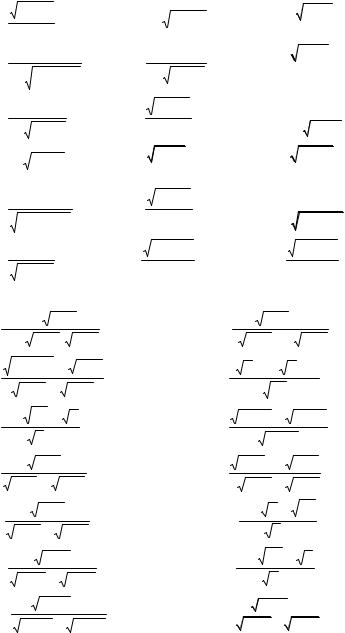
5.3.13. ∫ |
|
|
x2 − 9 |
dx . |
5.3.14. ∫ x |
3 |
|
|
9 − x |
2 |
dx . |
|
|
|
5.3.15. |
|
∫ |
|
x2 − 1 |
dx . |
||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|||||||||||||||||||||||||||
5.3.16. ∫ x 2 |
|
|
|
dx |
|
|
|
|
|
5.3.17. ∫ |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
5.3.18. |
∫ |
|
|
x2 − 9 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
(x2 − 1)3 |
. |
|
|
|
x2 − 1 . |
|
|
|
|
|
|
|
|
|
|
dx . |
|||||||||||||||||||||||||||||||
|
|
|
x2 |
|
|
|
|
|
|
|
|
x2 |
|
|
|
|||||||||||||||||||||||||||||||||||
5.3.19. ∫ |
|
|
|
|
|
|
dx |
|
|
|
|
. |
5.3.20. ∫ |
|
x2 − 9 |
dx . |
|
|
|
5.3.21. |
∫ |
|
|
|
dx |
|
|
|
|
|
. |
|||||||||||||||||||
x3 x2 − 1 |
|
|
x |
4 |
|
|
|
|
|
|
x2 |
x2 |
+ 9 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
5.3.22. ∫ x |
2 |
|
|
|
1 − x |
2 |
dx . |
|
5.3.23. ∫ |
|
x2 − 4 |
|
dx . |
|
|
|
5.3.24. |
∫ |
|
|
16 − x2 |
dx . |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
x |
4 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5.3.25. ∫ |
|
|
|
|
|
|
dx |
|
|
|
|
. |
|
5.3.26. ∫ |
|
x2 + 9 |
dx . |
|
|
|
5.3.27. |
∫ |
|
|
|
dx |
|
|
|
|
|
|
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
(x 2 + 9)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x2 + 4)3 |
||||||||||||||||||||||
5.3.28. ∫ |
|
|
x |
2 dx |
|
. |
|
|
5.3.29. ∫ |
16 − x |
2 |
dx . |
|
|
5.3.30. ∫ |
|
|
16 − x 2 |
dx . |
|||||||||||||||||||||||||||||||
|
|
9 |
|
− x2 |
|
|
|
|
|
x |
4 |
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
5.4. Find the integrals. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
5.4.1. ∫ |
|
|
|
|
1 − |
|
|
x + 1 |
|
dx . |
|
|
|
|
|
|
5.4.2. ∫ |
|
|
3 |
|
|
|
x + 1 − 1 |
|
|
|
dx . |
||||||||||||||||||||||
(1 + |
|
3 |
x |
+ 1) x |
|
|
|
|
|
|
|
( |
x |
+ 1 + |
1) x + 1 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
+ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
5.4.3. ∫ |
3 |
|
(x |
+ 1)2 + 6 x + 1 |
dx . |
|
|
|
|
|
|
5.4.4. ∫ ( |
3 |
x |
+ 1)( |
|
x + 1)dx . |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
x + 1 + |
|
|
|
x + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 x5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
5.4.5. ∫ x + |
3 |
|
|
2 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
5.4.6. ∫ |
|
|
2x + 1 + |
3 |
|
2x + 1dx . |
||||||||||||||||||||||||||
|
|
3 x |
|
|
+ |
|
|
x dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
x( |
|
x + 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x + 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
5.4.7. ∫ 3 |
|
|
|
|
|
|
x − 1 |
|
|
dx . |
|
|
|
|
|
|
5.4.8. ∫ |
|
|
x − 1 − 23 x |
− 1 |
dx . |
||||||||||||||||||||||||||||
|
x − 1 + |
6 |
|
x |
|
|
|
|
|
|
|
|
3 |
x |
− 1 + x − 1 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
− 1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
5.4.9. ∫ 3 |
|
x |
|
|
|
6 x − 1 |
|
|
dx . |
|
|
|
|
|
|
5.4.10. ∫ x + |
|
3 x + 3 x2 |
dx . |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
− 1 + x − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x( |
|
x + 1) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
5.4.11. ∫ 3 |
|
|
|
|
6 |
|
x |
+ 3 |
|
dx . |
|
|
|
|
|
|
5.4.12. ∫ x + |
3 |
|
2 |
+ |
6 |
x dx . |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 x |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
x + 3 + x + 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x( |
|
x + 1) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
5.4.13. ∫ |
|
|
|
|
|
|
|
3x + 1 − 1 |
|
dx . |
|
|
|
|
|
|
5.4.14. ∫ |
|
|
|
3x + 1 + 2 |
|
dx. |
|
|
|
||||||||||||||||||||||||
|
|
3x + 1 + |
3 |
3x + |
|
|
|
|
|
|
|
3 |
3x + 1 + |
|
|
3x + |
1 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
143 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
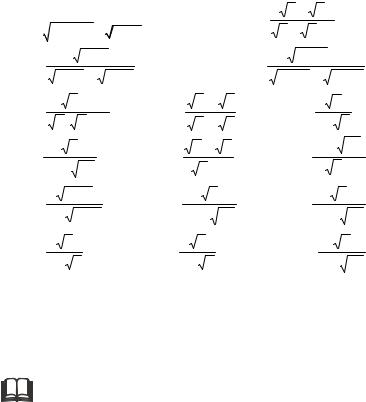
5.4.15. ∫ |
|
|
|
|
|
|
1 |
|
|
|
|
dx. |
|
|
|
|
5.4.16. |
∫ 3 |
x − 3 |
|
x |
|
dx . |
|
||||||||
3 (2x + 1)2 − 2x |
|
|
|
|
|
x − |
6 |
x − |
|
|
||||||||||||||||||||||
|
+ 1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||||||||||
5.4.17. ∫ 3 |
|
|
|
|
x + 3 |
|
dx . |
|
|
|
|
5.4.18. |
∫ |
|
6 |
3x + 1 + 1 |
dx . |
|||||||||||||||
x + |
3 + |
6 |
x |
|
|
|
|
|
|
3x |
+ 1 |
|
− |
3 |
|
3x + 1 |
||||||||||||||||
|
|
|
|
+ 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
5.4.19. ∫ |
|
|
|
x |
− 1 |
dx . |
5.4.20. ∫ |
3 |
|
x + |
6 |
x |
dx . |
|
5.4.21. ∫ |
|
|
|
|
x |
dx . |
|||||||||||
|
x ( |
3 |
|
|
|
|
|
x + |
x |
|
1 + |
4 |
||||||||||||||||||||
|
|
|
|
|
x + 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||||||||||
5.4.22. ∫ |
|
|
|
|
x |
|
dx . |
|
5.4.23. ∫ 4 x + |
|
x dx . |
5.4.24. ∫ |
|
x 6− 3 |
x2 |
dx . |
||||||||||||||||
|
|
3x + 3 x2 |
|
|
|
|
|
|
|
|
x + 1 |
|
|
|
|
|
|
|
x( |
|
x + 1) |
|||||||||||
5.4.25. ∫ |
|
|
x + 3 |
|
dx . |
5.4.26. ∫ |
|
|
x |
|
dx . |
5.4.27. ∫ |
|
|
|
|
x |
dx . |
||||||||||||||
1 |
+ |
3 |
x + 3 |
x |
− 43 x2 |
4x |
− 3 x2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
5.4.28. ∫ |
|
|
3x |
|
dx . |
|
|
5.4.29. ∫ |
|
|
|
4x |
dx . |
|
|
5.4.30. ∫ |
|
|
|
|
x |
dx . |
||||||||||
|
|
1 |
− |
|
|
x |
|
|
|
|
|
1 |
− |
x |
|
|
|
|
|
|
|
|
|
|
|
x |
− 3 x2 |
|
||||
Topic 6. Definite integrals
Definitions. Existence of the definite integral. Properties of the definite integral. The fundamental theorem of integral calculus by Newton-Leibniz. Basic methods of definite integrals application.
Literature: [1, section 7], [3, section 7, §2], [4, section 7, §23], [5, section 6], [6, section 9, ch. 9.1, 9.2], [7, section 11, §§1—6] [9, §§35—39].
Т.2 |
Main concepts |
6.1. Definitions
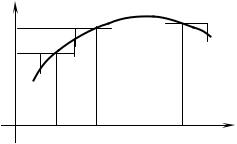
n
The sums of the form ∑ f (ξ i ) xi (Fig.2.1) were used to estimate certain
i=1
quantities such as area, mass, distance, and volume. The larger n is and the shorter the sections xi = xi − xi−1 are, the closer we would expect these
approximating sums to be to the quantity we are trying to find. We are really interested in what happens to these approximating sums as all the sections in the partition are chosen smaller and smaller. This leads to the notion of the definite integral of a function over an interval, which will be defined after we introduce a measure of the “fineness” of a partition.
Definition. The mesh of a partition is the length of the longest section (or sections) in the partition.
144
|
y |
|
|
|
|
|
|
|
|
y=f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(ξ2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(ξ1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О x0= |
|
a ξ1 |
|
x1 ξ2 |
|
x2 |
|
f(ξn) |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
xn-1 ξn xn=b x |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
Fig. 2.1 |
|
|
|
|
|
|||
Definition. |
If f (x) |
|
is a |
function |
defined on |
[a, b] |
and |
the |
sums |
|||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ f (ξi ) xi approach |
a |
certain |
number |
as the mesh |
of partitions |
of |
[a, b] |
|||||||||
i=1 |
|
|
|
|
|
|
|
|
|
sampling number ξi is |
chosen in |
|||||
shrinks toward |
0 (no matter how the |
|||||||||||||||
[xi−1 , xi ] ), that |
certain |
number |
is called |
the definite |
integral |
of |
f (x) |
over |
||||||||
[a, b] . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The numbers a and b are called limits of integration; a is the lower limit and b is the upper limit. The symbol x is called the variable of integration and f(x) is
the integrand. |
|
The definite integral is also called the definite integral of f (x) |
from a to b |
and integral of f (x) from a to b. The symbol for this number is ∫b |
f (x)dx . The |
a |
|
symbol ∫ comes from the letter S of Sum; the dx traditionally suggests a small |
|
section of the x axis and will be more meaningful and useful later. It is important to realize that area, mass, distance traveled, and volume are merely applications of the definite integral. (It is a mistake to link the definite integral too closely with one of its applications, just as it narrows our understanding of number 2 to link it always with the idea of two fingers.)
Slope, velocity, magnification, and density are particular interpretations or applications of the derivative, which is a purely mathematical concept defined as
limit: |
x)− f (x) |
|
|
f′(x) = lim |
f (x + |
. |
|
|
|
||
x→0 |
x |
||
Similarly, area, total distance, mass, and volume are just particular interpretation of the definite integral, which is also defined as limit:
b |
n |
∫ f (x)dx = meshlim→0 |
∑ f (ζi ) xi . |
a |
i=1 |
145 |
|

In advanced calculus it is proved that, if f(x) is continuous, then
n
lim ∑ f (ζ i ) xi
mesh→0 i=1
exists; that is, a continuous function always has a definite integral. For emphasis we record this fact, an important result in advanced calculus, as a theorem.
Theorem. Let f(x) be a continuous function defined on [a, b]. Then the approximating sums
n
∑ f (ξi ) xi
i=1
Approach a single number as the mesh of the partition of [a, b] approaches 0.
Hence ∫b |
f (x)dx exists. |
|
|
|
a |
|
|
|
|
||
|
Geometrical interpretation of the definite integral. If f(x) is |
||
|
continuous and f(x) ≥ 0 on [a,b] then ∫b |
f (x)dx can be interpreted as |
|
|
|
a |
|
the area of the region bounded by the curve y = f(x), the x-axis and the lines x = a and x = b, as indicated in fig. 2.1
6.2. Properties of the definite integral
Let f(x) and g(x) be continuous functions ant let λ1 and λ2 be the constants. |
||||||||||
Then |
|
|
|
|
|
|
|
|
|
|
1. If |
f (x) ≥ 0 |
|
|
|
|
|
|
|
||
|
|
|
|
b |
||||||
|
|
|
|
∫ f (x)dx ≥ 0 . |
||||||
2. If ( a < b ) in [a; b] , then |
a |
|||||||||
|
|
|
|
|
|
|
||||
|
|
|
b |
|
|
b |
||||
|
|
|
|
|||||||
|
|
|
∫ f (x)dx |
|
≤ ∫ |
|
f (x) |
|
dx . |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||
3. If |
f (x) ≤ g(x) for all x |
|
a |
|
|
a |
||||
in [a; b] ( a < b ), then |
||||||||||
|
|
|
b |
|
|
b |
||||
|
|
|
∫ f (x)dx ≤ ∫ g(x)dx . |
|||||||
aa
4.If the limits of integration are equal, we have
a
∫ f (x)dx = 0 .
a
146
ba
5.∫ f (x)dx = − ∫ f (x)dx .
ab
|
b |
b |
b |
|
6. |
∫[f (x) ± g(x)]dx = ∫ f (x)dx ± ∫ g(x)dx . |
|
||
|
a |
a |
a |
|
|
b |
b |
b |
b |
7. |
∫ λ1 f (x)dx ± ∫ λ 2 g(x)dx = λ1 ∫ f (x)dx ± λ 2 ∫ g(x)dx . |
|||
8. |
a |
a |
a |
a |
If a, b and c are numbers, then |
|
|
||
|
|
b |
c |
b |
|
|
∫ f (x)dx = ∫ f (x)dx + ∫ f (x)dx . |
||
9. |
|
a |
a |
c |
If m and M are numbers and m ≤ f (x) ≤ M |
for all x in [a; b] (), then |
|||
b
m(b − a) ≤ ∫ f (x)dx ≤ M (b − a) if a < b ,
a
and m(b − a) ≥ ∫b f (x)dx ≥ M (b − a) if a > b.
a
10. If a and b ( a < b ) are numbers. Then there is a number c between a and b such that
b
∫ f (x)dx = f (c)(b − a) .
a
A number f(c) is called a mean-value of f(x) in [a, b].
|
a |
a |
11. а) |
∫ f (x)dx = 2∫ f (x)dx , if f (x) is an even function; |
|
|
−a |
0 |
|
a |
|
b) |
∫ f (x)dx = 0 , if f (x) is an odd function. |
|
−a
12.∫b f (x)dx = ∫b f (t)dt.
a |
a |
The variable of integration is a “dummy variable” in the sense that any other variable produces the same result, that is, the same number.
13. If f (x) has integral in [a, b] and x [a; b] , then
x
а) Ф(x) = ∫ f (t)dt exists and is continuous in [a, b] ;
|
|
a |
x |
||
|
d |
|
d |
||
b) |
Ф(x) = |
∫ f (t)dt = f (x) . |
|||
dx |
dx |
||||
|
|
|
|
a |
|
|
|
|
|
147 |
|
6.3. Evaluating definite integrals
6.3.1. The fundamental theorem of integral calculus by Newton-Leibniz
This section shows that there is an intimate connection between the definite integral and the derivative. This relationship, expressed in the fundamental theorem of integral calculus by Newton-Leibniz, provides a tool for computing many, but not all, definite integrals without having to form a single approximating sum. The argument will be intuitive.
Fundamental theorem. If f (x) is continuous on interval [a, b] and F(x) is any antiderivative of f (x) there, then
b
∫ f (x)dx = F(b) − F(a) .
a
Usually, F(b) – F(a) is abbreviated by writing
|
b |
|
b = F(b) − F(a). |
|
|
∫ f (x)dx = F(x) |
|
||
|
a |
|
a |
|
|
|
|
|
|
The substitution method and integration by parts are the most general |
||||
techniques. |
|
|
|
|
6.3.2. Substitution technique for a definite integral |
||||
Let f(x) be a continuous |
function on the interval [a, b], x = ϕ(t) be a |
|||
differentiable function on the interval [α; β] , and ϕ(α) = a , ϕ(β) = b , then |
||||
|
b |
β |
||
|
∫ f (x)dx = ∫ f (ϕ(t))ϕ′(t)dt . |
|||
|
a |
α |
||
6.3.3. Integration by parts
The integration by parts of definite integral is made according to the formula:
b |
b |
b |
|
∫udv = uv |
a |
−∫vdu, |
|
a |
a |
||
|
where u and v are the differentiable functions of x on the interval [a, b].
|
Typical problems |
Т.6 |
|
|
|
Evaluate the given definite integrals. 1. ∫1 (3x2 − 2x + 3)dx.
−2
Solution. Here f(x) = 3x2 − 2x + 3, a = − 2; b = 1. Since an antiderivative of 3x2 − 2x + 3 is F(x) = x3 − x2 + 3x, then:
148
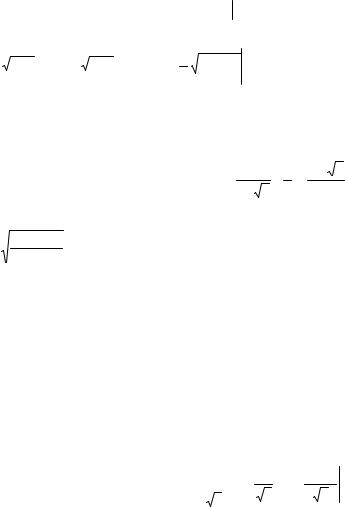
∫1 (3x2 − 2x + 3)dx = F(1)− F(− 2)= (1− 1+ 3)− (− 8 − 4 − 6)= 21. |
|
If we−2had chosen F(x) to be |
x3 − x2 + 3x + C, then F(1) − F(−2) = |
= ((1− 1+ 3)+ C)− ((− 8 − 4 − 6)+ C) |
= 21, as before. Since the choice of the value |
of C is immaterial, for convenience we shall always choose it to be 0, as
originally done. Usually F(b)−F(a) is abbreviated by writing: F (x) |
|
|
ba. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Hence we have ∫1 (3x2 − 2x + 3)dx = (x3 − x2 + 3x) |
1− 2 = |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− 2 |
|
|
= (1 |
− 1 + 3) − (− 8 − 4 − 6) = 21. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
3 |
|
|
|||||
2. ∫ 3 1− xdx = − ∫ 3 1− xd (1− x) = − |
|
3 (1− x)4 |
= − |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4 |
|
0 |
|
|
(0 − 1) |
= |
|
. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4 |
4 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
|
1+ tg2 x |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
3. ∫ |
|
|
|
|
|
|
|
|
dx = ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
∫ |
|
|
|
|
|
|
|
|
d(1+ tg x) = |
|
|
||||||||||||||||||||||||
(1+ tg x) |
2 |
(1+ tg x) |
2 |
|
|
cos |
2 |
x |
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
π |
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
π (1+ tg x) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
+ 1 = 2 − 3 . |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
= − |
|
|
|
|
|
|
|
|
|
3 |
|
= − |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
= |
|
− |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
+ tg x |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
1+ 3 |
2 |
|
|
|
2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ tg 3 |
|
|
|
1+ tg 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
1− cos 2x |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
4. ∫ |
dx |
= ∫ |
sin x |
dx = |
|
∫sin xdx + |
|
∫ (− sin x)dx = |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
= − cos x |
π |
+ cos x |
|
3π |
= −(−1− 0) + (0 − (−1)) = 2 . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5. Find the mean-value of |
f (x) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
in [2; 3]. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
Solution. By property 10 |
|
|
|
|
|
|
|
|
x 2 − x + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (c) = |
|
|
|
|
|
|
|
∫ f (x)dx , |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
− a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
where f (c) is the mean-value of |
|
f (x) in |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
[a; b] , c [a; b] . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We have |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
d x − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x − 1 |
3 |
|
|||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||
f (c) = |
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
= ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
arctg |
= |
|||||||||||||||||||||||||||||||
3 |
− |
2 |
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
3 |
|
|
2 |
|
3 |
|
|
|
|
3 2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
− x + 1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
149 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
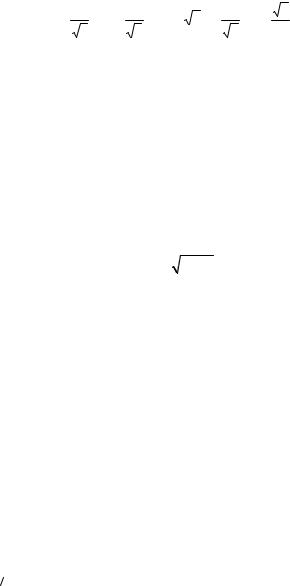
= |
|
2 (arctg 5 − arctg |
3) = 2 arctg |
3 . |
||||||
|
|
|
|
|
3 |
3 |
3 |
|
9 |
|
Used a formula |
arctg α − arctg β = arctg |
α − β |
. |
|
||||||
|
|
|||||||||
|
|
|
|
|
|
|
1+ αβ |
|
||
|
|
π |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||
6. Show that ∫ (x4 − x2 ) tg xdx = 0 . Do not evaluate the definite integral. |
||||||||||
|
− π |
|
|
|
|
|
|
|
||
4 |
|
|
of |
integration are |
symmetrical |
to zero, namely if |
||||
Solution. Limits |
||||||||||
f (x) = (x4 − x2 ) tg x |
is odd, by property 11 the given integral is equal to 0. We |
|||||||||
have: |
|
|
|
|
|
|
||||
f (− x) = ((− x)4 − (− x)2 ) tg(− x) = −(x4 − x2 ) tg x = − f (x) , |
||||||||||
consequently, f (x) is the odd function. |
|
|
|
|
||||||
7. Show that the substitution is not used |
x = sin t to obtain the integral |
|||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
∫ x 3 1−x2 dx . |
|
|||
Solution. Domain of t |
0 |
|
|
|
[−1; 1] , however the |
|||||
is (−∞; ∞) correspondent x |
||||||||||
interval of the integral is [0; 2] . Therefore, do not use the substitution x = sin t
to obtain the integral
In Problems 8 to 10 use the substitutions to evaluate the given definite integrals.
4 x2dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8. I = ∫ |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x=4 |
|
|
|
|
|
|
x=4 |
|||
|
|
|
|
|
|
t = x3 |
− 1; |
|
|
dt |
|
1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Solution. Case 1. |
I = |
|
|
|
|
2 |
|
|
|
= |
|
|
|
∫ |
|
= |
|
ln |
t |
= |
||||
|
dt = 3x |
dx; |
3 |
t |
3 |
|||||||||||||||||||
|
|
|
|
|
|
|
x=2 |
|
|
|
|
x=2 |
||||||||||||
|
|
|
|
1 |
|
|
|
|
|
4 |
|
1 |
(ln 63 − ln 7)= |
|
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
= |
ln |
x3 − 1 |
|
= |
|
ln 9. |
|||||||||||||||
|
|
|
3 |
3 |
3 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Case 2. Since t = x3 − 1, when x = 2 we have t = 7 when x = 4
|
|
|
1 |
63 |
|
dt |
|
1 |
|
|
|
|
|
63 |
1 |
(ln 63 − ln 7)= |
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
t = 63. Thus I = |
∫ |
= |
ln |
|
t |
|
|
|
= |
ln 9. |
||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
π 2 |
dx |
3 |
7 |
|
t |
|
|
3 |
|
|
|
|
|
|
7 |
3 |
|
3 |
|
||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9. ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 + cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Solution. The substitution |
tg |
= t |
transforms the integral to |
|
|
||||||||||||||||
2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
|
|
|
||
