Зацерковний В.І. та ін. ГІС та бази даних

8.2.3. Двовимірні об’єкти

До двовимірних об’єктів відносяться область, внутрішня область,

полігон (рис. 8.7).

Внутрішня

область

Рис. 8.7. Ілюстрація двовимірних об’єктів

Область – безперервний об’єкт, який має певні межі. Внутрішня область – область, яка не має власної межі. Полігон (багатокутник, ареал, контур, область) – двовимірний

(площинний) об’єкт, у якого внутрішня область утворена замкненою послідовністю дуг.

Сукупність полігонів утворює полігональний шар.

8.2.4. Тривимірні об’єкти

До тривимірних об’єктів відносяться об’ємне геометричне тіло, що має три виміри (довжину, ширину, висоту).

Рис. 8.8. Ілюстрація тривимірного об’єкта

271

8.3. Подання просторових об’єктів у векторній моделі

Векторна структура – це подання просторових об’єктів у вигляді набору векторів (координатних пар), що описують геометрію об’єктів.

При роботі з паперовою (аналоговою) картою користувачі мають справу з координатами, які використовуються для вимірювання відстаней на карті, або визначають координати за допомогою лінійки. Проте на картах реальні координати спроектовані на площину. Ці координати вказують на реальні місця земної поверхні в певній системі координат, що визначаються різними картографічними проекціями. Місце розташування кожного об’єкта на карті описується рівнянням:

F = f(x, y, z, n1, n2,…nn),

де: x, y – координати точок, які визначають місцезнаходження об’єкта; z – висота об’єкта над рівнем моря;

n1, n2,…nn – атрибутивні дані об’єкта.

У векторній моделі подання географічних (просторових) об’єктів виконується за допомогою відображення їх геометричної форми на двовимірній площині з використанням елементарних графічних примітивів

(рис. 8.9):

–точок (нульмірних векторів);

–ліній (поліліній, утворених плоскими двовимірними векторами);

–областей (форм, обмежених полігонами – замкненою послідовністю двовимірних векторів). Геооб’єкти, що подаються областями, називають

полігональними об’єктами.

Рис. 8.9. Векторне подання геооб’єктів графічними примітивами

272

Для визначення положення об’єктів на карті з місцями земної поверхні використовується декартова система координат (x, y). Кожна точка визначається однією парою координат (x, y). Лінії або дуги описуються впорядкованою системою координат (x, y), фігури – послідовністю координат (x, y) відрізків ліній, які визначають відрізки ліній, що обмежують фігуру.

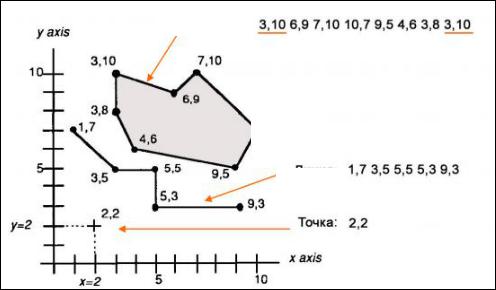
Користуючись координатною системою, можна подати точки, лінії і полігони у вигляді списку координат, а не малюнка або креслення. На рис. 8.10 пари координат (2,2) описують положення точки, пари коорди-

нат (1,7; 3,5; 5,5; 5,3; 9,3) – лінію (дугу), а пари координат (3,10; 6,9; 7, 10; 10,7; 9,5; 4,6; 3,8; 3,10). Збіг першої і останньої пари координат означає, що полігон замкнений.

Перша й остання пари координат полігона однакові, оскільки полігон завжди замкнений. Ці списки координат показують, яким чином об’єкти карти зберігаються комп’ютером у вигляді наборів пар чисел х, у.

Полігон

Лінія

Точка

Рис. 8.10. Подання об’єктів у векторній формі

Власне, звідси і походить термін "цифрування" (digitalization), який означає введення даних паперової карти в комп’ютер, тобто перетворення аналогових даних (analog data) на цифрові (digital data).

Концептуальним тут є те, що геооб’єкти у комп’ютері зберігаються як файли координатних пар (наборів). Табличні списки координатних пар є формою подання плоских цифрових файлів.

Реальні ГІС мають справу не з абстрактними лініями та точками, а з об’єктами, які включають лінії й ареали, що займають певне просторове положення і мають доволі складні взаємозв’язки. Тому повнофункціональна векторна модель даних ГІС повинна відображати просторові об’єкти як сукупність [22]:

273

–геометричних (метричних) об’єктів, поданих у вигляді точок, ліній і полігонів;

–атрибутів;

–зв’язків між об’єктами.

Кожному об’єкту векторного зображення може відповідати запис у базі даних, чим досягається прив’язка інформації до місцевості. За наявності двох або більше географічних об’єктів кожному з них присвоюється ідентифікаційний (порядковий) номер (рис. 8.11).

Ідентифікатор – унікальна характеристика просторового об’єкта, що присвоюється конкретному об’єкту користувачем або інформаційною системою і яка використовується для фіксації координатних та адресних даних просторових об’єктів.

Використання ідентифікатора відкриває широкі можливості для перегляду й аналізу просторової інформації, з’являється можливість при- в’язки до об’єкта певної тематичної (атрибутивної) інформації, яка може міститись в одній чи декількох внутрішніх або зовнішніх базах даних.

Об’єкти у векторній моделі подаються у вигляді невпорядкованої послідовності записів, кожний з яких включає (рис. 8.12):

–ідентифікатор об’єкта;

–значення координати х;

–значення координати y.

Рис. 8.11. Векторні моделі подання Рис. 8.12. Подання об’єктів у векторній множини географічних об’єктів формі з використанням

ідентифікатора

На базі перерахованих вище графічних примітивів (точка, лінія, полігон) будується будь-яка векторна модель просторових даних. Цієї сукупності елементарних графічних об’єктів цілком достатньо для опису форми як лінійних, так і просторових картографічних об’єктів, які кодуються у вигляді сукупності координат точок, що апроксимують форму лінійного

274

об’єкта, наприклад, адміністративного кордону, русла річки або контуру (кордону) територіального об’єкта, території землекористування населеного пункту, басейну річки тощо.

Точкові геооб’єкти, зображені на рис. 8.11, подаються таблицею координатних пар, що представлені в табл. 8.1.

Лінійні геооб’єкти, зображені на рис. 8.11, подаються таблицею послідовностей координатних пар, що представлені в табл. 8.2.

Полігональні геооб’єкти, зображені на рис. 8.11, подаються таблицею послідовностей координатних пар, що представлені в табл. 8.3.

Таблиця 8.3

Таблиця полігональних географічних об’єктів

Усю сукупність векторних моделей поділяють на два типи:

–нетопологічні, які не відображують зв’язків між об’єктами, а описують тільки їх геометрію (шейп-файли ArcView, модель "Спагеті");

–топологічні, які дозволяють одержувати вичерпну інформацію про взаємовідношення між геометричними примітивами без зміни координат просторових об’єктів (векторна топологічна модель, модель DIME, модель "Дуга-вузол", геореляційна модель, TIN-модель, покриття ГІС

ARC/INFO) [86].

275

8.4. Нетопологічні (прості) векторні моделі

8.4.1. Модель "Спагеті"

Метод подання лінійних об’єктів у вигляді неупорядкованого набору лінійних об’єктів, які описують тільки їх геометрію, отримав назву модель "Спагеті" (spaghetti model), оскільки не має апарату опису топологічних відношень між лінійними об’єктами та їх елементами. Такі подання, як відомо, називаються нетопологічними векторними моделями. На рис. 8.13 представлена модель "Спагеті", яка, по суті, переводить "один в один" графічне зображення карти.

Рис. 8.13. Нетопологічна модель "Спагеті"

У цієї моделі відсутній опис відношень між об’єктами, а кожний геометричний об’єкт зберігається окремо і не пов’язаний з іншими, наприклад, межа об’єктів 25 та 26 (рис. 8.13) записується двічі за допомогою однакового набору координат. Усі відношення між об’єктами повинні розраховуватись незалежно, що ускладнює аналіз даних і збільшує обсяг інформації, яка зберігається в базі даних.

Опис сутностей спагетної моделі векторних даних, зображених на рис. 8.13, представлено в табл. 8.4.

Таблиця 8.4

Опис сутностей спагетної моделі векторних даних

Назва "спагетна" на перший погляд звучить дивно, хоча насправді вона досить точно характеризує суть моделі. Якщо уявити собі покриття кожного графічного об’єкта паперової карти у вигляді шматочків "спагеті", то кожний із них є примітивом: дуже короткі – для точок, більш довгі – для відрізків прямих, набори відрізків, з’єднаних кінцями, – для меж областей (полігонів). Тобто за допомогою примітивів ("спагеті") різної довжини можна описати будь-який просторовий об’єкт.

У цій моделі області, що межують між собою, мають різну довжину "спагеті" для опису загальних сторін. Не існує областей, для яких будь-який ланцюг "спагеті" був би спільним. Кожна сторона кожної окремої області має свій унікальний набір ліній і пар координат. Хоча зрозуміло, що спільні сторони областей, навіть будучи записаними окремо в комп’ютер, мають однаковий набір координат, що призводить до надлишковості внесеної до комп’ютера інформації внаслідок подвійного проходження по загальних для двох суміжних полігонів межах. Це спричиняє значне збільшення витрат часу на введення даних, а також появу двох меж просторових об’єктів, які не збігаються внаслідок неточностей позиціонування дигітайзера.

Ця модель подання векторних даних була характерна для початкового періоду розвитку ГІТ і не враховувала взаємного розташування просторових об’єктів (топологічність об’єктів), а отже, не дозволяла виконати багато видів аналізу.

8.4.2. Шейп-файли

Шейп-файл – це нетопологічна структура даних, яка не зберігає топологічні відношення в явному вигляді. Однак, на відміну від інших спрощених графічних структур даних, полігони у шейп-файлі подаються у вигляді однієї або декількох ланок (rings).

Ланка – це замкнута петля, яка не перетинається. За допомо-

гою такої структури можна представляти складні (складені) структури (полігони, що містять у собі "острови" (пустоти)). Вершини ланки розташовуються (нумеруються) послідовно в напрямку за ходом годинникової стрілки, при цьому область справа за ходом руху вздовж межі ланки буде знаходитись усередині даного полігона, а область, що ліворуч, – за даним полігоном (рис. 8.14).

Оскільки полігональні об’єкти у форматі шейп-файлу можуть складатися з однієї або декількох частин, то в цьому форматі можуть бути подані об’єкти, що складаються з окремих частин, що не змикаються або які перекриваються. Наприклад, окрема земельна ділянка, що розділяється дорогою, може бути представлена або у вигляді двох окремих полігонів за допомогою двох ланок і двох записів у таблиці атрибутів, або як один полі-

277

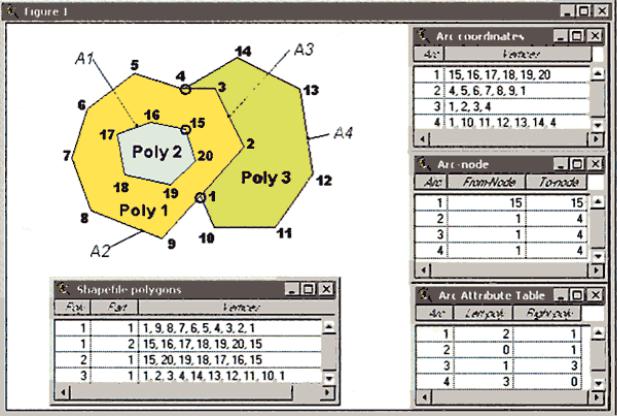
гон, що складається з двох частин з одним записом у таблиці атрибутів. Через це частину користувачів може ввести в оману той факт, що використання деяких команд ArcView GIS може привести до створення просторово розрізнених об’єктів,які складаються з декількох частин.

Рис. 8.14. Полігони в шейп-файлі

Головною перевагою шейп-файлів є те, що ця проста структура файлів забезпечує більш швидку візуалізацію порівняно з покриттями. Можливо, саме тому структура даних у вигляді шейп-файлів була розроблена для ArcView GIS – програмного забезпечення, первісно призначеного швидше для відображення даних, а не для їх аналізу. Крім того, шейпфайли легко копіювати, при цьому не потрібно їх експортувати, що вимагається для файлів формату .e00. Специфікація шейп-файлів доступна, і більшість програмних продуктів їх підтримують. Через це цими причинами шейп-файли стали провідним стандартом обміну геоданими.

Топологічні структури даних, що притаманні сучасним ГІС, забезпечують більш логічний (автоматизований) шлях для проведення цифрування, виправлення похибок і артефактів; дозволяють скоротити об’єм даних по полігонах, що зберігаються, оскільки межі між суміжними полігонами не дублюються; а це забезпечує ефективний просторовий аналіз таких відношень, як суміжність, зв’язність і включення.

278

Примітка. Поширеною оманою щодо шейп-файлів є те, що, використовуючи їх, неможливо знаходити суміжні об’єкти, оскільки топологія в них відсутня. Проте суміжні об’єкти можуть бути з легкістю виявлені за перетинанням цільових полігонів з іншими полігонами на тій же карті та ідентифікації точок перетину полігонів, які стосуються меж або накладаються на них. Геометричні перетини суміжних об’єктів миттєво виявляються шляхом порівняння вершин суміжних об’єктів, а не шляхом пошуку суміжних полігонів у таблиці. Наприклад, для того щоб знайти всі ділянки, що прилягають до досліджуваної ділянки, треба обрати цю ділянку, обрати опцію "Вибрати темою" з меню "Тема", вказати "перетинають" зі спадаючого вікна і клацнути на кнопці "Нова вибірка", щоб вибрати всі ділянки, що прилягають до первісно обраної ділянки.

Більш складний аналіз суміжності (сусідства) можна провести, об’єднуючи вибірку темою із запитом специфічних атрибутів, таких як ідентифікація тільки житлових ділянок, що прилягають до промислових зон. Хоча більш складні типи суміжності, які включають напрям (наприклад, пошук суміжних ділянок на схід від заданої дороги), доволі важко виявити без створення топології. Однак подібні варіанти аналізу застосовуються не дуже часто і не завжди є критично важливими для пересічних користувачів.

8.4.3. Точкова полігональна структура

Сукупність трьох елементарних графічних об’єктів – точки, лінії та полігона – є цілком достатньою для опису форми як лінійних, так і просторових картографічних об’єктів, які в цьому випадку кодуються як сукупність координат точок, що апроксимують форму лінійного об’єкта, наприклад, адміністративного кордону, русла річки тощо, або контуру (межі) територіального об’єкта, наприклад, території землекористування населеного пункту, басейну річки.

Векторне подання просторових об’єктів у вигляді точок називають точковою полігональною структурою (point polygon structure) [15]. Первісно таке подання даних з’явилося в системах автоматизації проектування (CAD-системах) і в простих графічних пакетах.

Форма або образ просторового об’єкта точковою полігональною моделлю подається точками, розміщених у місцях зміни форми.

У базі даних у цьому випадку зберігається пооб’єктна інформація про координати точок введення (рис. 8.15). У структуру атрибутивних таблиць вводиться описова інформація про геооб’єкти, що цифруються, а також інформація про графічне зображення об’єктів на карті.

Цей різновид векторних структур просторових даних відповідає початковому періоду розвитку ГІТ, хоча деякі сучасні ГІС і сьогодні використовують цей формат. Прикладом може бути формат MIF/MID – MapInfo Data Interchange Format – відкритий обмінний формат пакета MapInfо, а також шейп-файли (shapefiles) фірми ESRI [50].

279

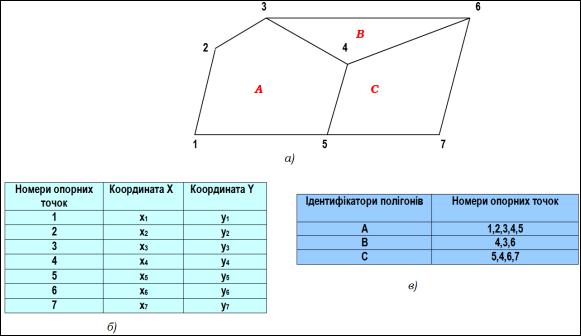
Рис. 8.15. Подання геооб’єктів з використанням точкової полігональної структури:а – формалізація вихідної карти; б – таблиця координат опорних точок; в – таблиця атрибутів полігонів

Основний недолік цього способу формалізації просторових даних полягає у відсутності в запису даних топологічної інформації (інформації про взаємне розміщення об’єктів), що вимагає при введенні метричних даних за допомогою дигітайзера проводити повний обхід кожного полігона. Це призводить до подвійного проходу по спільних для двох суміжних полігонів межах, що обумовлює значне збільшення витрат часу на введення, а також появу двох, що не збігаються через неточності позиціонування дигітайзера, спільних меж суміжних просторових об’єктів, які створюють так звані "паразитні"полігони [50].

Цей спосіб подання часто також називають "спагеті".

8.4.4. Лінійна полігональна структура

Основні типи координатних даних у класі векторних моделей можуть визначатись і через базовий елемент "лінія".

Векторне подання просторових об’єктів у вигляді ліній називають лінійною полігональною структурою (line polygon structure).

Усі просторові об’єкти у лінійній полігональній структурі складаються з ліній. Наприклад, куб можна зобразити шістьома зв’язаними прямокутниками, кожний з яких утворюється чотирма зв’язаними лініями, або можна представити куб у вигляді дванадцяти зв’язаних ліній, що утворюють ребра цього куба (рис. 8.16).

280